明晰學段要求，踐行單元教學
——以“與三角形有關的角”單元起始課為例

☉山東省泰安市泰山學院附屬中學 賈貞鋒

當前不少版本的初中數學教材上關于“與三角形有關的角”的教學都安排了多個課時，并且第1課時都是安排三角形的內角和的教學，第2課時安排直角三角形兩銳角互余，并由此拓展得出三角形外角的性質.根據教學實際，一般后續還會安排2節課開展與三角形的角相關的習題教學.最近我們在研習全國著名特級教師李庾南老師相關著作、文獻資料時發現，李老師及其團隊倡導的“三學”（即學材再建構、學法三結合、學程重生成）對一線教師的課堂教學設計與組織有著直接的指導價值.本文課例就是以“三學”為指導，整合教材，對三角形的角的教學進行教材重組，實施的“與三角形有關的角”單元教學的起始課.

一、“與三角形有關的角”單元教學起始課

教學環節（一）復習引入

引導語：前面我們剛學習了三角形的有關概念，與三角形有關的重要線段，我們也知道了三角形中兩個重要元素：邊和角.本節課開始，我們就來學習與三角形有關的角.

問題1：三角形共有幾個內角？這些內角之間有怎樣的數量關系？

預設：3個內角，它們的和為180度.接下來安排學生進行實驗活動.

活動：在小學同學們就知道了三角形內角和為180度，你們也通過剪拼的方法進行了驗證，請大家拿出課前準備的三角形紙板，小組合作再做一次剪拼三角形內角和為180度的實驗吧！

教學組織：學生剪拼之后，安排一個小組派一個代表上臺演示（如圖1到圖2），大家確認三角形內角和為180度之后，進入內角和定理的證明環節.

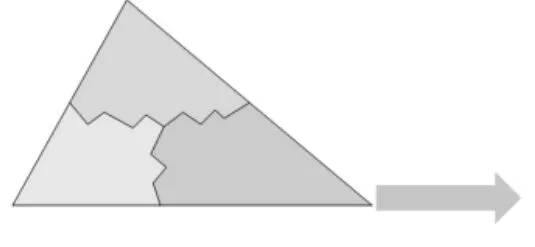
圖1

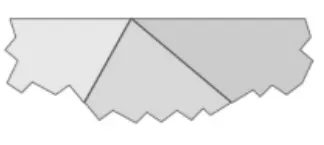
圖2

教學環節（二）證明定理與成果擴大

過渡：同學們剛剛回顧了小學里如何用拼圖法驗證三角形的內角和為180度，作為一種實驗確認是可以的，但數學的特點在于不滿足于實驗確認和直觀感知，需要走向一般進行推理證明.接下來大家畫出三角形，寫出已知求證，嘗試證明吧，建議同學們先獨立思考、證明，再在小組內交流各自的證明方法，最后我們再挑選小組代表分別上臺進行全班交流.考慮到課堂時間有限，我們在課上只安排學生展示如下兩種典型的證明方法（如圖3，圖4）.

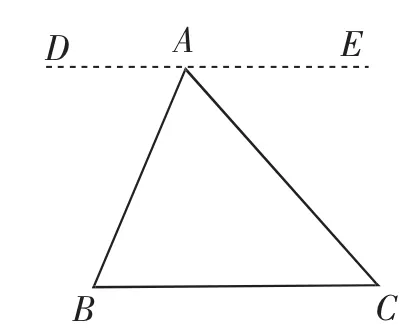
圖3

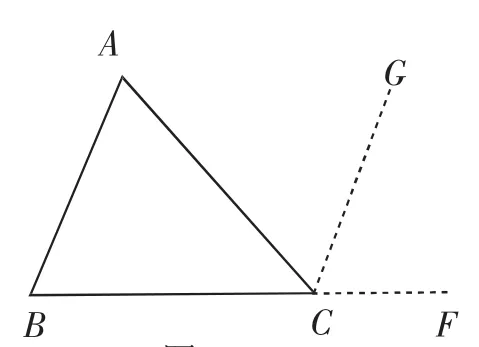
圖4

證明之后，教師板書三角形內角和定理及符號表示，并提醒學生三角形內角和定理揭示了三個內角之間的一個等量關系，只要知道兩個角的度數，就可以求出第三個內角的度數，進一步安排學生舉例，小組之間分別舉例求度數.

問題2：同學們手頭的直角三角板，大家研究一下，它們的角有什么數量關系？

預設：直角三角形的兩個銳角互余.這里注意到直角三角板是比較特殊的三角形，但只要是一般直角三角形，都可以利用三角形內角和推出兩個銳角的互余關系.教學時引導學生辨析從特殊走向一般的數學思想.

問題3：上面研究了直角三角形兩個銳角互余的情況，對于數學問題的學習與研究，我們常常在原命題研究之后，還可進一步逆過來想，即思考它的逆命題.那么當一個三角形有兩個內角具有怎樣的數量關系時，它是直角三角形呢？

預設：學生可能會有不同的理解，比如：

三角形中兩個內角互余時，第三個內角為直角；

三角形中兩個內角的和恰等于第三個內角時，該三角形為直角三角形；

三角形中兩個內角的差恰等于第三個內角時，該三角形為直角三角形.

當學生給出這些命題之后，教師需要追問如何證明，引導他們利用新學的三角形內角和性質進行證明.

問題4：同學在證明三角形內角和定理時，用到了圖4這樣的基本圖形，這里涉及到三角形的外角，如∠ACF，由三角形一邊的延長線與三角形一邊形成的角，稱為三角形的外角.大家想想，三角形的一個外角與內角之間有怎樣的數量關系？

預設：一個外角與相鄰的內角是互補的關系；三角形的一個外角等于和它不相鄰的兩個內角的和.這里學生發現之后，教師通過簡要的追問，讓學生說出證明思路即可，不過多展開細節，因為本課教學內容較多，教師只需及時把學生的發現整理到板書相關位置即可.

以上的問題3、問題4可以看成是對三角形內角和定理的成果擴大.

教學環節（三）例題教學

過渡：前面大家的探究成果很豐富，也舉例進行了一些練習，下面老師也帶來一個題組，幫助同學們鞏固新知.

例題：如圖5，在△ABC中，∠BAC=40°，∠B=75°.

圖5

（1）求∠C的度數.

（2）設點D為邊BC上一點，連接AD，當AD為△ABC高時，你能求出圖形哪些角的度數？

（3）在（2）的基礎上，再畫另一條高CE，設它們交于點O，求∠AOC的度數.

（4）將前面所探究的兩條高改成兩條角平分線AD，CE，此時還能求∠AOC的度數嗎？

教學組織：這一組題通過PPT漸次呈現，前一問學生解出之后安排學生講解思路，教師引導學生參與評析，然后再呈現下一問題.其中第（4）問可以根據課堂教學時間相機呈現，如果時間偏緊，學生在解答前面的問題時用時較多，則第（4）問留作課后挑戰.

教學環節（四）小結提升

課堂小結時，把黑板上一些知識內容用框架線完善起來（圖6為板書示意圖）.

注意，板書中提到的“三角形的外角和為360°”在前面教學中沒有涉及，這是安排在全課小結的一個精心設計.

圖6

引出板書中三角形外角和為定值的探究問題，安排學生思考三角形的外角和為多少度？如何證明？最后形成完善的知識框架體系（在板書中補出“三角形的外角和為360°”）.

我們以PPT給出著名數學家陳省身先生的一段話：“人們常說，三角形內角和等于180°，但是，這是不對的！”

老教授對這句話作了精辟的解釋：說“三角形內角和為180°不對，不是說這個事實不對，而是說這種看問題的方法不對，應該說“三角形外角和是360°”！

二、教學立意的進一步闡釋

（一）深刻理解教學內容，明辨學段要求，精準設定教學目標

三角形相關的角在小學階段就學過，并且學生已經知道三角形的內角和為180度，這些都不能簡單的在初中課堂上重復、空轉，應當快速通過，基于深刻理解教學內容的高度，引導學生認識到實驗、操作、直觀獲得的經驗和結果，還需要進行推理證明，這也是數學的特點.基于以上認識，我們確定了本課的教學目標就是證明三角形內角和定理，并由三角形內角和性質出發，推理直角三角形兩銳角互余的性質；掌握三角形外角性質與外角和為360度的性質.而考慮到教學時間的限制，例習題的教學不是本課的主要任務，所以我們只安排了一個題組進行訓練，在后續教學中再進行相關的例習題訓練.

（二）精心預設課堂小結，構建知識框架，相機變式拓展提升

不少老師的課堂小結以“今天我們學到了什么，掌握了什么知識或方法，你有什么經驗與同學們分享？”之類的套話來小結.我們從這節課例的構思中發現，可以在小結階段對本課所學的知識、性質或定理進行框架式的構建，完善、充實相關內容，讓學生通過課堂小結知曉本課所學知識的大致框架、脈絡，并且根據學情進行適當的拓展提升.比如，課堂最后，我們通過數學家陳省身先生的名言引出了外角和的性質.這種性質將對應著后續學生會學到的任意多邊形的外角和為定值（一個周角）.

三、寫在后面

簡單的內容如何教得深刻、教出新意，是值得我們認真思考的，我們關于三角形的相關角教學起始課只是一次積極的嘗試，期待老師們圍繞相關課題開展同課異構，豐富這個課題的課例研究.