“學材再建構”：讓綜合實踐活動課充滿智慧的聲音

黃娟

[摘 要] 基于學情、教材的現狀，對學材進行再建構是備課的高標準和要求，也是真正實現以學定教、按需施教的要求之一. 筆者基于數學教學中的綜合實踐活動課，談談如何以“中心四邊形”的教學為例，達成學材再建構、素養真提升的效果.

[關鍵詞] 學材；再建構；綜合實踐；智慧；核心素養

“學材再建構”源自全國名師李庾南的“自學·議論·引導”教學法，是根據各種主客觀因素，對顯性和隱性的學材進行加工和重組，以實現學習效益的最大化，更好地服務于學生. 其依據是學生各方面的準備情況，包括學生的整體水平、綜合素質、心理狀況等，出發點是使重組的學材更適應學生的發展. 筆者在一次綜合實踐活動公開課中基于“學材再建構”對“中點四邊形”（蘇教版《義務教育教科書·數學》八年級下冊）進行了設計和教學，教后感想頗多，以下結合教學片段談談筆者的感想.

教學分析

“中點四邊形”是“平行四邊形”這一章中引申出的內容，課本中沒有專門的具體教材呈現，但“中點四邊形”是一個常用的幾何模型，在后續幾何學習及中考中有一定的出現頻率，為平面幾何性質的探究提供依據和方法. 因此，筆者將它作為綜合實踐活動課的素材進行教學.

中點四邊形是利用三角形中位線推導得到，因此三角形的中位線定理是本節課的預備知識. 只要掌握一般四邊形的中點四邊形形狀就容易推導出特殊四邊形的中點四邊形形狀，因此本節課的學習內容難度系數不大，完全可以放手讓學生自己探究. 鑒于以上兩點，筆者將本節課的教學目標設計如下：

1. 體會中點四邊形的形成過程，知道中點四邊形的形狀和原四邊形形狀的關系.

2. 理解中點四邊形形狀的判斷及證明方法，并學會中點四邊形在幾何中的實際運用.

3. 感受合作探究的過程，體悟類比方法的魅力，學會分析問題的一般方法，初步形成合作意識.

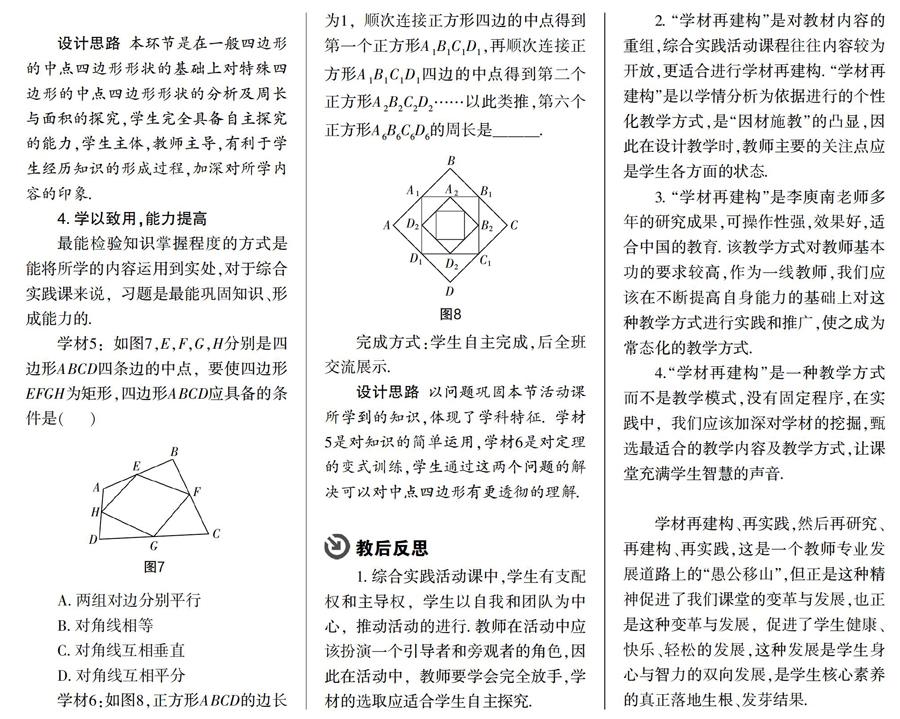
完成方式：學生自主完成，后全班交流展示.

設計思路 以問題鞏固本節活動課所學到的知識，體現了學科特征. 學材5是對知識的簡單運用，學材6是對定理的變式訓練，學生通過這兩個問題的解決可以對中點四邊形有更透徹的理解.

教后反思

1. 綜合實踐活動課中，學生有支配權和主導權，學生以自我和團隊為中心，推動活動的進行. 教師在活動中應該扮演一個引導者和旁觀者的角色，因此在活動中，教師要學會完全放手，學材的選取應適合學生自主探究.

2. “學材再建構”是對教材內容的重組，綜合實踐活動課程往往內容較為開放，更適合進行學材再建構. “學材再建構”是以學情分析為依據進行的個性化教學方式，是“因材施教”的凸顯，因此在設計教學時，教師主要的關注點應是學生各方面的狀態.

3. “學材再建構”是李庾南老師多年的研究成果，可操作性強，效果好，適合中國的教育. 該教學方式對教師基本功的要求較高，作為一線教師，我們應該在不斷提高自身能力的基礎上對這種教學方式進行實踐和推廣，使之成為常態化的教學方式.

4.“學材再建構”是一種教學方式而不是教學模式，沒有固定程序，在實踐中，我們應該加深對學材的挖掘，甄選最適合的教學內容及教學方式，讓課堂充滿學生智慧的聲音.

學材再建構、再實踐，然后再研究、再建構、再實踐，這是一個教師專業發展道路上的“愚公移山”，但正是這種精神促進了我們課堂的變革與發展，也正是這種變革與發展，促進了學生健康、快樂、輕松的發展，這種發展是學生身心與智力的雙向發展，是學生核心素養的真正落地生根、發芽結果.