深刻理解教學內容，踐行“學材再建構”
——從“分式方程增根問題”教學說起

☉江蘇省海安市城南實驗中學 陳愛軍

最近一次教研活動中，筆者聽了青年教師執教的一節“分式方程的增根與無解問題”習題課，對該課題的相關問題有了深入的思考.本文先概述該課的教學片段，再圍繞分式方程的增根與“方程同解原理”給出一些闡釋，供研討.

一、“分式方程的增根與無解問題”習題課教學片段

教學片段1：復習舊知，引入新課.

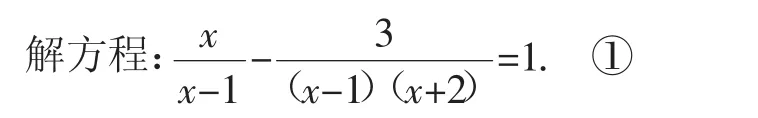
學生解方程，一個學生上臺板演.

解：方程兩邊同乘（x-1）（x+2），得x（x+2）-3=（x-1）（x+2）. ②

解這個方程，得x=1.

檢驗：當x=1時，（x-1）（x+2）=0，所以原分式方程無解.

學生解好后核對答案，教師講評前先在黑板上標注了方程①、方程②.

師：x=1是分式方程轉化為整式方程的解，但它使最簡公分母等于0，因此它不是原分式方程的解.像這樣，我們稱x=1是原方程的增根.請同學們自己總結什么是增根.

生1：它是整式方程的解，并且使最簡公分母等于0.

師：回答得很好！再請同學們思考：為什么會產生增根呢？

眾生靜靜思考，1分鐘后，沒有學生能回答，教師“自答”.

師：因為原方程①中未知數x的取值范圍是x≠1且x≠-2，而去分母化為整式方程②時，方程兩邊同乘了一個等于零的整式，未知數x的取值范圍擴大為全體實數.這樣，方程②的解就有可能不是方程①的解.可見，從方程①變形為方程②，這種變形并不能保證兩個方程的解相同.所以，解分式方程一定要檢驗.

學生求解，一個學生上臺板演.

解：方程兩邊同乘（x+1）（x-1）.

整理得：（5-k）x=-1.

由原分式方程“可能有增根”，令最簡公分母（x+1）·（x-1）=0，得x=±1.

將x=±1代入，解得k=4或k=6.

所以當原分式方程有增根x=1時，k=6；當原分式方程有增根x=-1時，k=4.

教師組織學生核對解答后繼續給出一道變式題.

學生先練習，然后教師巡視過程中挑中一個學生上臺板演.

解：方程兩邊同乘（x+1）（x-1）.

整理得：（5-k）x=-1 ①.

若原分式方程無解，可能是產生了增根，令最簡公分母（x+1）（x-1）=0，得x=±1.

將x=±1代入①，解得k=4或k=6.

所以當k=4或k=6時，原方程無解.

針以上述漏解，教師進行訂正，引導學生觀察方程①，這個整式方程也可能出現無解的情況，即當k-5=0時，整式方程出現無解的情形，所以這道變式題的“無解”并不只對應著分式方程可能產生增根的情況.綜上，原分式方程無解時，k=4、k=5或k=6.

二、分式方程為什么會產生增根

讓我們先從方程求解的根據說起，解方程的過程無非是不斷地用新方程替代舊方程直到新方程是一個或幾個形如x=a的方程時為止的替代過程，在這個過程中，只有逐步替代的方程的解集總和被替代方程的解集完全相同時，才能保證最后一個或幾個形如x=a的方程的解集與原方程的解集相同，才能既不產生增根，也不減少根的個數.

這里再鏈接“舊人教版”教材上關于同解方程、同解變形及原理的有關表述：我們把解集相同的方程叫同解方程，把方程變形為與它必同解的方程叫同解變形，把方程變形為未必與它同解（即有時同解，有時不同解）的方程的變形叫非同解變形.為了徹底弄清解方程時方程變形的理論，我們再列出有關同解變形的幾個原理：

原理1：方程兩邊都加上（或都減去）同一個整式，所得方程與原方程是同解方程；

原理2：方程兩邊都乘（或都除以）同一個不為0的數，所得方程與原方程是同解方程；

原理3：方程兩邊都乘同一個含有未知數的整式，所得方程的解可能比原方程的解多，從而造成增根；

原理4：方程兩邊都除以同一個含未知數的整式，所得方程的解可能比原方程的解少，從而造成失根；

原理5：方程兩邊同時乘方相同的次數，所得方程的解可能比原方程的解多，從而造成增根.

可見，原理1、2是同解變形，原理3、5是可造成增根的非同解變形，而原理4則是可能造成失根的非同解變形.

查閱現行人教版七年級上冊教材，關于方程解法的依據是以“等式性質”給出的，而等式的性質2表述為“等式兩邊同乘一個數，或除以一個不為0的數，結果仍相等”，這與“同解原理2”是不同的.

現在來看分式方程是怎樣轉化為整式方程的.如果我們能夠將方程變形，使得去掉分母，就能使分式方程化為整式方程，用已知的整式方程的求解方法求解.為了完成這種變形，不可避免地要應用原理3，兩邊同乘分母的最小公倍式，與此同時，破壞了方程的同解性，驗根則是不可避免的.接下來值得思考的就是，怎樣驗根才是最簡便的？想清楚去分母這一步驟的潛在風險之后，就知道驗根其實就是檢驗這一步驟是否滿足同解原理，從而確認分式方程的驗根只要代入最簡公分母就可以了.

三、關于數學知識深刻理解的進一步思考

1.深刻理解教學內容，“知其然，知其所以然”

傅種孫先生說，教學需要追求讓學生“知其然，知其所以然”.要實現這樣的教學品質，前提是教師本人不斷加深對教學內容的深刻理解，也就是旅美數學教育學者馬立平博士所指出的，追求數學知識理解的深度、廣度、貫通度.就上文提及的分式方程的增根問題，我們不但要讓學生知道需要驗根，還要讓優秀學生理解為什么需要驗根，這種驗根并不是簡單地檢驗計算有無粗心、錯漏，而是對解法依據的完善與檢查，是必不可少的步驟，也是數學科學、嚴謹的體現，上升到這樣的高度來幫助學生理解，不只是訓練了分式方程的增根問題的求解，更是對學科素養的熏陶.

2.研習不同版本教材，在對比優選中重組“學材”

專家教師李庾南老師近年來提出“學材再建構”，主張基于數學知識深理解的角度對教學內容重組后呈現，倡導開展單元教學，讓學生先見森林、再見樹木.在觀摩研習李老師很多課例的過程中，我們發現李老師很多教學課例并不囿于某一種版本教材，而是融會貫通，對比不同教材并優選重組學材.筆者曾多次參與李庾南實驗學校的教研活動，像上文分式方程增根問題的教學，李老師在自己的班級上教七年級學生一元一次方程時，就曾給她的學生補充過方程同解變形及相關原理，這樣到了八年級再教學分式方程時，她班的學生就很自然地想到解分式方程的各步依據是否符合同解變形，當存在風險時，就會想到需要進一步驗證、確認，這也就提示我們，在平時的備課活動中，手頭不只是準備一種版本的教材，而要收集不同版本的教材，并時時研習、對比，以便在對比后優選形成更適合本班學情的“學材”.

3.專業研判增設課時，引導學生重視相關內容

一個教學現實是，目前數學課時是遠遠大于教材內容課時的，實際教學中會有相當多的習題課、復習課、試卷講評課，這些課堂教學的研究遠遠沒有得到應有關注.我們在一些隨堂聽課中更多的是看到就題講題，比如，針對家庭作業選用的教輔資料的講評訂正，針對階段檢測、單元檢測、期中檢測、期末檢測試卷的講評.像上文中以分式方程的增根問題增設一節習題課的做法在日常教學中也是常態，教師并沒有因為教材上沒有相關內容就弱化對這些教學內容的要求.我們希望上文中分式方程增根問題的教學，不只是因為各級考試中對分式方程增根習題的“現實引領”，更重要的是教師能站在理解數學的高度，基于方程同解變形、原理的角度促進學生想清辨明、想深想活.