從勾股定理逆定理的證明談構造法

☉山東省萊蕪市雪野旅游區雪野鎮中心中學 魏衍彬

引例 如圖1，△ABC的三邊長a、b、c滿足a2+b2=c2，求證：△ABC是直角三角形.

證法1：如圖2，作Rt△A′B′C′，使B′C′=a，A′C′=b，∠C′=90°.

在△ABC和△A′B′C′中，BC=a=B′C′，AC=b=A′C′，AB=c=A′B′，所以△ABC △A′B′C′.所以∠C=∠C′=90°，即△ABC是直角三角形.

證法2：如圖3，過點B作BD⊥BC，且使BD=b，連接CD.

在Rt△DBC中，由勾股定理，得CD2=BC2+BD2=a2+b2=c2，所以CD=c=AB.

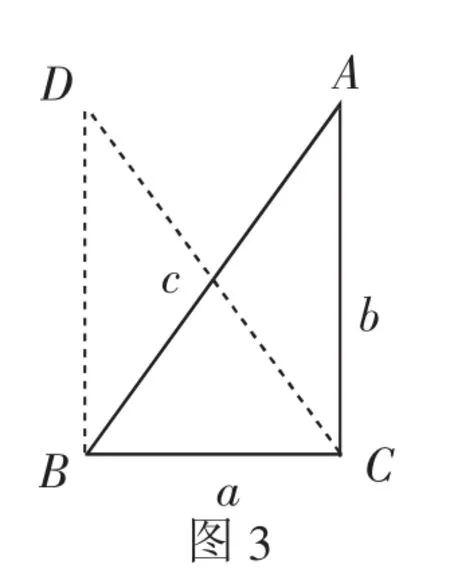
在△ABC和△DCB中，AC=b=BD，CD=c=AB，BC為公共邊，所以△ABC△DCB.所以∠ACB=∠DBC=90°，即△ABC是直角三角形.

以上是勾股定理逆定理的證明，無論是證法1還是證法2，基本思路都是通過構造一個直角三角形，然后運用勾股定理并結合已知條件證明兩個三角形的第三邊相等，進而利用“邊邊邊”證明兩個三角形全等，最后根據“全等三角形的對應角相等”使命題得證.這里滲透了一種重要的數學方法：構造圖形法.構造圖形法是一種重要的解題方法，許多看似復雜，用常規方法難以解決的數學問題，如果能夠根據題目中的數或式的結構特征，發掘隱含的數或形的信息，借助于形式聯想，巧妙地構造出圖形，可使問題獲得別開生面的解決.下面以例說明構造法在數學解題中的應用，以期對讀者有所幫助.

一、構造一元二次方程

由方程根的定義可知，若x1≠x2，且c=0，則x1、x2是一元二次方程ax2+bx+c=0（a≠0）的兩根；若x+x=則x、x是一元二次方程1212的兩根；若a（x-x1）（x-x2）-m=0（a≠0），則x1、x2是一元二次方程a（x-x1）（x-x2）-m=0的兩根.可以據此構造一元二次方程解決一類與之相關的問題.

例1 設a1、a2、b1、b2都是實數，a1≠a2，且有（a1+b1）·（a1+b2）=1，（a2+b1）（a2+b2）=1，求（a1+b1）（a2+b1）的值.

在提升生物教學質量的過程中，教師應充分認識到實驗教學的重要性，在教學過程中，以理論知識為主，實踐教學為輔，帶領學生進行實踐教學，進而增強學生對理論知識深度理解。例如：在講解“綠葉中色素的提取和分離”的過程時，由于本節課為實驗課，在展開實驗之前，教師可以向學生明確相應的教學目標，讓學生明確綠葉中色素的種類和作用。在確定教學目標后，可讓學生進行簡單的預習，并按照課本中的知識研究無法理解的問題，在進行實踐教學的過程中，教師可以對學生進行自主教學，以便培養學生的探索創新能力。然后再帶領學生進行生物實驗，鍛煉學生的動手實踐能力，這對于提升生物課堂教學質量具有良好的作用。

分析：觀察兩個已知等式，我們發現這兩個等式是具有相同結構的等式：（x+b1）（x+b2）=1，因此可以通過構造一元二次方程（x+b1）（x+b2）=1求解.

解：構造一元二次方程（x+b1）（x+b2）=1.

因為（a1+b1）（a1+b2）=1，（a2+b1）（a2+b2）=1，且a1≠a2，所以a1、a2是一元二次方程（x+b1）（x+b2）=1，即（x+b1）（x+b2）-1=0的兩根.

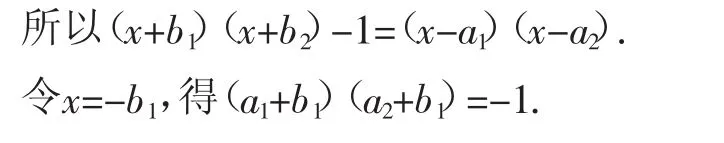
例2 已知實數a、b、c、d滿足a-b=c-d和ab=cd，判斷實數a、b、c、d的關系并說明理由.

分析：先將ab=cd變形為a（-b）=c（-d），即可逆用韋達定理構造一元二次方程求解.

解：將ab=cd變形為a（-b）=c（-d），且設a-b=c-d=m，a（-b）=c（-d）=n，根據一元二次方程根與系數的關系可知a、-b和c、-d都是一元二次方程x2-mx+n=0的兩根.所以a=c，-b=-d，或a=-d，-b=c.即a=c，b=d或a=-d，b=-c.

說明：本題除了構造法之外，還有一種比較巧妙的方法：二元代換法.由a-b=c-d，可設a=m+p，b=-m+p，c=m+q，d=-m+q，代入ab=cd，得p2-m2=q2-m2.所以p2=q2.所以p=q或p=-q.當p=q時，a=c，b=d；當p=-q時，a=-d，b=-c.

二、巧構等腰直角三角形

等腰直角三角形是比較特殊的三角形，它具有直角三角形和等腰三角形兩者的特性，它的每一個銳角都等于45°.在解決一類求角度問題時，如果能夠根據題目特征巧妙構造出等腰直角三角形，利用等腰直角三角形的性質求解十分簡捷.

例3 如圖4，表示3×1的正方形網格.連接AF、AQ，求∠AFB+∠AQB的度數.

分析：∠AFB和∠AQB都不是特殊角，無法求出它們的具體度數.可先用量角器分別量出這兩個角的大小，然后計算它們的和大約等于45°，因此我們可以大膽猜想，∠AFB+∠AQB應該等于45°.由45°聯想到構造等腰直角三角形求解.

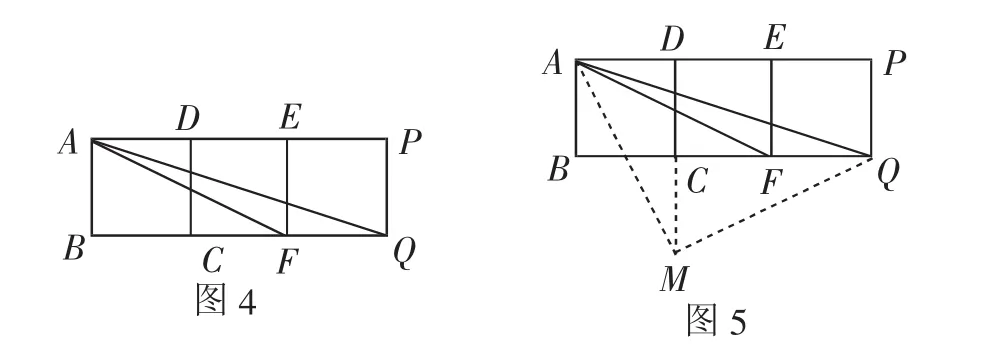
思路1：如圖5，延長DC至CM，使CM=CD，連接AM、QM.

易證△ABF △MCQ △ADM.于是∠AFB=∠MQC=∠AMD，AM=QM，所以∠AMQ=∠AMD+∠QMC=∠MQC+∠QMC=90°.所以△AMQ是等腰直角三角形.所以∠AFB+∠AQB=∠MQC+∠AQB=∠AQM=45°.

思路2：如圖6，作正方形BKMN，連接AM、MF.易證△ABQ △MKF，△ABF △MNA.所以∠AQB=∠MFK，∠MAN=∠AFB，AM=AF.所∠MAF=∠MAN+∠BAF=∠AFB+∠BAF=90°.所以△AMF是等腰直角三角形.所以∠AFB+∠AQB=∠AFB+∠MFK=∠AFM=45°.

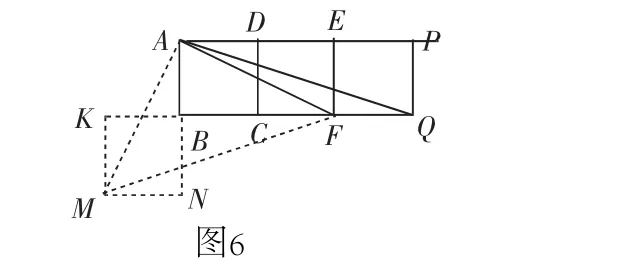
說明：本題構造方法較多，除了上面介紹的兩種構造方法，還有其他構造方法.這些構造法的實質是將△ABF和△ABQ拼在一起，使△ABF的頂點F和△ABQ的頂點Q重合，邊BF和BQ在一條直線上且在重合頂點的同側，而邊AF和AQ在BF（或BQ）的異側.

三、構造正方形網格

在學習平面直角坐標系時，我們會遇到一類求正方形網格內的三角形的面積問題.由于這些三角形的邊長多為無理數且為斜三角形，無法直接利用三角形的面積公式求解.我們的辦法是采用分割法，將三角形的面積轉化為規則圖形的面積之和或差求解.這就啟發我們，在解決一類邊長為無理數的三角形的面積問題時，有時可以通過構造正方形網格的辦法求解.

分析：由勾股定理的逆定理知，△ABC是一個斜三角形，而且三邊都是無理數，這使得求△ABC的面積變得非常困難.仔細觀察三角形的三邊特征，注意到5=1+4=12+22，10=1+9=12+32，13=4+9=22+32，聯想到勾股定理和平面直角坐標系中求幾何圖形面積的方法，于是可先構造一個正方形網格（每個小正方形的邊長為1），再在網格中畫出格點△ABC（即△ABC三個頂點都在小正方形的頂點處），這樣不需求△ABC的高，而借用網格就能計算出它的面積.

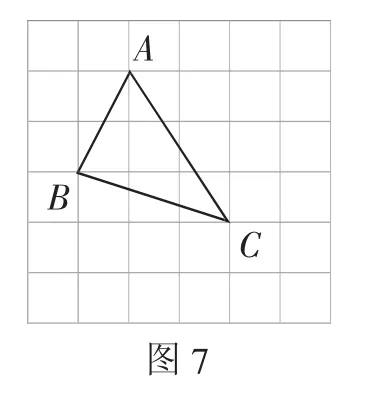
解：如圖7所示，構造一個正方形網格（每個小正方形的邊長為1），在網格中畫出格點△ABC，由勾股定理，得AB=×3=9-2-1.5-3=2.5.

從上面可以看出，在解答一些具有明顯數字結構特征或圖形特征的數學問題時，如果能夠根據題目特點，靈活構造式子或圖形求解，這樣可以化腐朽為神奇，收到事半功倍、出奇制勝之效，同時對培養同學們的創新思維也大有裨益.當然，可以用構造法解決的數學問題遠不止這些，只要同學們認真體會，勤于思考，善于發現，用心總結，一定會將這種方法變成我們的解題利器.