聚焦數(shù)學思想培養(yǎng)的小學數(shù)學課堂研究

董旭妹

摘 要：數(shù)學思想是數(shù)學的靈魂，教師在備課中探尋數(shù)學思想，在課堂的探究過程中巧妙滲透數(shù)學思想，讓學生領(lǐng)會數(shù)學思想的妙用，把握數(shù)學學習的靈魂。結(jié)合筆者的實際教學，就小學數(shù)學課堂數(shù)學思想的培養(yǎng)作淺顯探索。

關(guān)鍵詞：數(shù)學思想；滲透；課程

《義務(wù)教育數(shù)學課程標準》（以下簡稱《標準》）中指出：“課程內(nèi)容既要反映社會的需要、數(shù)學學科的特征，也要符合學生的認知規(guī)律。它不僅包括數(shù)學的結(jié)論，也應(yīng)包括數(shù)學結(jié)論的形成過程和數(shù)學思想方法。”《標準》已將數(shù)學基本思想納入義務(wù)教育階段的數(shù)學學習目標，所以，教師要領(lǐng)悟“標準”的變化，從思想上提高對數(shù)學思想滲透重要性的認識，在課堂中把握課堂環(huán)節(jié)，適當滲透數(shù)學思想，使得學生知識和思想方法的雙豐收。

一、滲透數(shù)學思想，有序?qū)胄抡n

“引入環(huán)節(jié)”是一節(jié)完整課堂教學不可缺少的環(huán)節(jié)，它猶如電影的“序幕”，對于新授環(huán)節(jié)的教學有著重要的作用。

1.無聲轉(zhuǎn)化，舊知引新知

課伊始，教師可以抓住新舊知識之間的聯(lián)系，創(chuàng)設(shè)合理的情境，讓學生在搭建知識建構(gòu)的橋梁中，進行合理的遷移、轉(zhuǎn)化，進而進入新知識的探究中去。在學習“三角形的面積”前，教師可以請學生回憶之前學習過哪些圖形的面積，讓學生在復(fù)習平行四邊形的面積后，想一想三角形能否轉(zhuǎn)化為平行四邊形，使學生在三角形和平行四邊形之間建構(gòu)橋梁。

2.數(shù)形、分類，概念教學更暢通

小學階段學生是以形象思維為主，認知水平不高，他們的思維離不開生活中具體事物。在學習“方程”時，我們首先讓學生觀察演示天平上左右兩盤的物體，將形象的事物用抽象的算式表示；然后再請學生將匯總的算式進行分類（按照是等式還是不等式分一分，并在后面標注出是否含有字母）。讓學生在數(shù)形思想和分類思想的引導(dǎo)下，對這些算式有了一定的認識，為后面方程概念的總結(jié)提供了有力的證據(jù)。

二、滲透數(shù)學思想，精彩探究新知

數(shù)學是知識和思想方法的有機融合，在課堂教學中，教師要注意找到兩者之間的聯(lián)系，在學生探究知識的過程中，適時滲透數(shù)學思想方法，使學生感受數(shù)學思想在具體問題中的存在，感知數(shù)學思想在解決問題中的意義。

1.滲透符號化思想

符號化思想主要是指運用符號去表達研究的對象，恰當?shù)姆柨梢郧逦乇硎境鰯?shù)學概念和事物之間的邏輯關(guān)系等。符號化思想在小學數(shù)學內(nèi)容中隨處可見。在教學“平行四邊形的面積”時，學生通過剪拼，發(fā)現(xiàn)平行四邊形和長方形的聯(lián)系，總結(jié)出平行四邊形的面積=底×高，把面積公式變成符號化的語言就是S=ah，明確a、h表示的意義，知道用符號化的語言表示這類公式更簡潔，從而使學生了解、建立符號化思想。

2.滲透統(tǒng)計的思想

“統(tǒng)計”就是搜集、整理、計算和分析有關(guān)研究對象的數(shù)據(jù)，制作相應(yīng)的表格、圖形，并作出適當?shù)耐茢唷Ｔ趯W習“可能性”時，讓學生拋硬幣，統(tǒng)計出現(xiàn)正面和背面的次數(shù)；學習“平均數(shù)”時請學生統(tǒng)計本班學生的身高和體重，填寫統(tǒng)計表；學習“扇形統(tǒng)計圖”時讓學生統(tǒng)計本班學生愛好，制作統(tǒng)計圖……以上都是在滲透統(tǒng)計的數(shù)學思想。

3.滲透對應(yīng)、極限思想

“對應(yīng)”反映的是兩個集合的元素間的關(guān)系。一年級教學“多與少”時，教師可以出示生動直觀的動物卡片：上面是4只小雞，下面是3只小兔子，問“哪種動物多”，引導(dǎo)學生將兩種動物一一對應(yīng)，發(fā)現(xiàn)小雞還多著一只，所以小雞多。就這樣，學生在比較的過程中感受一一對應(yīng)。

在“認識自然數(shù)”中，在數(shù)軸上標注出一個一個的點，并在點處標注上0、1、2、3……讓學生從一一對應(yīng)的點和數(shù)中發(fā)現(xiàn)：自然數(shù)都能用數(shù)軸上一個一個的點表示，沒有最大的自然數(shù)，自然數(shù)無限多……對應(yīng)、極限思想無形中滲透到課堂中。

4.滲透數(shù)形結(jié)合的思想

數(shù)形結(jié)合思想方法是指將數(shù)與式的代數(shù)信息和點與形的幾何信息互相轉(zhuǎn)換。“數(shù)缺形時少直觀，形少數(shù)時難入微。”這句話足以證明“數(shù)形結(jié)合”在數(shù)學中的重要地位。

在教學“有余數(shù)的除法”過程中，教師可以讓學生拿出自己的學具小棒，動手分擺，根據(jù)擺分的結(jié)果列出相應(yīng)的算式。用生活中的實際事物，幫助學生理解除法算式中的平均分的過程，就這樣，“數(shù)”在實實在在的“形”中得到理解，問題在“形”的擺分中得到解決。

三、滲透數(shù)學思想，讓練習效果斐然

數(shù)學知識的鞏固，技能的形成，智力的開發(fā)，能力的培養(yǎng)等需要適量的練習才能實現(xiàn)。學生數(shù)學思想方法是否掌握，需要學生在練習中進行驗證。

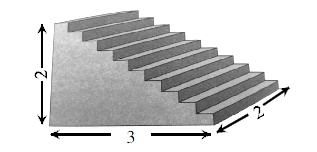
在學習了“平行四邊形”后的練習中，有一題目：樓梯臺階上鋪著地毯（如下圖），你能計算出最少需要多少平方米的地毯嗎？這道練習需要用轉(zhuǎn)化思想將圖形進行變形，得到地毯的長其實就是臺階側(cè)面的一個長和一個高的總和。講解時，教師要在圖中進行線段的平移，將轉(zhuǎn)化的過程進行詳細地演示，讓學生真正明白地毯的長究竟為什么是5米，將轉(zhuǎn)化思想內(nèi)化于心。

思想是數(shù)學的靈魂，不管是概念的建立、數(shù)學公式的發(fā)現(xiàn)，還是數(shù)學問題的解決，核心在于數(shù)學思想方法的滲透和建立。在新課改的要求之下，教師也要在教學理念和教法上進行改變，深研教材，提高思想方法滲透的自覺性，讓學生的數(shù)學思維能力得到切實有效的發(fā)展，從而提高學生的數(shù)學素養(yǎng)。

參考文獻：

楊慶余.小學數(shù)學課程與教學[M].高等教育出版社，2004.