小表格 大作用
郁蓉

[摘要]表格在小學數學課堂中的運用十分廣泛,無論是信息整理,還是數學思考,或是規律探索,都可以借助表格來“說話”,強化學生對所學知識的理解。教學中教師可引導學生運用表格整理信息,幫助學生分析問題、解決問題,讓學生學會數學思考,感悟表格的魅力和精彩,從而實現“教”與“學”的相得益彰。
[關鍵詞]表格;小學數學;運用
[中圖分類號]
G623.5
[文獻標識碼]A
[文章編號] 1007-9068( 2019)35-0050-02
表格是一種可視化的教學模式,也是組織、整理數據的有效助手。在數學課堂中,教師應注重表格的運用,讓學生通過表格這個知識載體,分析數量關系,探尋數學規律,尋找解決問題的有效策略,感受列表的重要性和優越性,從而使學生學有動力、學有方向、學有方法。
一、列表,實現信息整理
題目關鍵信息是審題的基本抓手,也是順利解答題目的關鍵。有時題目中的信息量比較多,學生難以厘清它們之間的關系,無法形成有效的解題思路,這時,運用列表的方法,對題目中的信息進行收集、整理,就有助于學生分析數量關系,找到有效的解題方法,提升解題的效率。
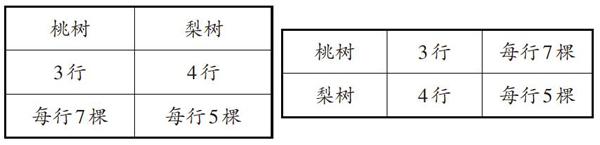
例如,“小芳家栽了3行桃樹、8行杏樹、4行梨樹,桃樹每行7棵、杏樹每行6棵、梨樹每行5棵,桃樹和梨樹一共有多少棵?”很顯然,題目中的數學信息比較多,應對題目中有用的信息進行相應整理。在自主嘗試的過程中,很多學生對題目中的條件、問題進行了摘錄和整理,但并沒有得到其他同學的認可,他們認為不夠簡潔。于是教師引導學生用列表的方法整理信息。(如下表所示)
學生通過觀察表格,認為可以從條件想起,先分別算出栽的桃樹和梨樹的棵數,然后相加;也有學生認為可以從問題想起:要求桃樹和梨樹一共多少棵,應分別算出桃樹和梨樹各有多少棵,從而使得問題得到順利解決。至此,學生從中領略到了列表整理信息的意義。
二、列表,實現自主探索
傳統的教學模式因為過分依賴對傳遞技術的關注,往往會扼殺學生的想象力和創造力,忽視學生能動性和自主性的發揮。對此,教師應變“灌輸講解”為“主動探索”,讓學生在探索中生成問題,進而分析問題、解決問題,達到“不憤不啟,不悱不發”的境界。
例如,在教學“年、月、日”時,教師讓學生在課前準備了很多不同年份的年歷。新課伊始,教師讓學生拿出準備的年歷,統計各個月的天數,然后填人下表中。
學生很快就完成了統計,教師引導學生將不同年份的統計表放在一起,然后小組交流各自的發現,學生發現,每年都有12個月,1月、3月、5月、7月、8月、10月、12月的天數都是固定的,都是31天,4月、6月、9月、11月的天數也是固定的,都是30天,只有2月是一個善變的月份,有時是28天,有時是29天,這是什么原因呢?學生的心中產生了大大的“?”號,從而驅動學生進入新一輪的探索,獲取知識的本質。
上述案例,教師針對教學內容引入表格,幫助學生收集相應的信息,并引導學生自主歸納得出大小月、2月的天數,進一步豐富學生對年、月、日的感性認識,為學生探索新知注入了活力。
三、列表,實現有序思考
小學高年級學生已經具有一定的整理信息、分析問題的能力,但他們思考通常處于無序的狀態,這樣的思維方式只能滿足于簡單問題的解決,對于難度大一些的題目,學生經常無所適從,不知如何下手。因此,教師應適時地引入表格,幫助學生對相關數據進行整理,做到不遺漏、不重復,更好地培養學生思維的嚴謹性和深刻性。
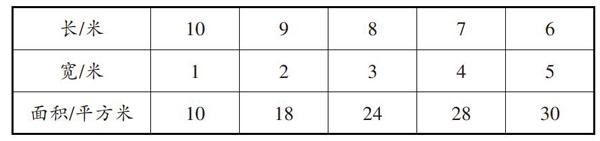
例如,在教學“一一列舉”時,對于例題:“王大叔用22根1米長的木條圍一個長方形花圃,怎樣圍面積最大?出示例題后,教師提出問題:依據題目中的條件和問題,你能想到什么?學生提出:不管怎樣圍,所圍長方形花圃的周長都是22米.而且長和寬都應該是整米數。在此基礎上,教師讓學生用小棒動手圍一圍,然后組織學生進行匯報:有學生說可以圍成長6米、寬5米的長方形,也有學生說可以圍成長10米、寬1米的長方形,還有學生說可以圍成長8米、寬3米的長方形……顯然,學生的回答是零散的,容易出現遺漏和重復的情況,不利于結論的得出。于是,教師引入了如下表格:
這時,讓學生觀察表格,就顯得非常的清晰,當所拼長方形花圃長6米、寬5米時,面積最大。但教師并沒有止步于此,而是提問:“觀察表格,你還有什么發現?”學生發現:當周長相等時,寬的長度接近于長,此時面積最大。在比較中,學生感受到了有序思考的價值和意義。
四、列表,實現規律探索
“規律”是蘇教版教材中的重要教學內容,也是學生學習的難點之一,因此很多學生“望而卻步”。如何幫助學生輕松地探尋規律是廣大教師值得思考的問題。而通過表格幫助學生探尋規律,是表格作用最直接的體現。因此,在引導學生尋找規律時,可以配合使用表格,讓學生更好地發現數與數之間的關系,尋找出其中的規律,提升數學綜合能力。
例如,教學“長方體和正方體的表面積和體積”后,教師出示題目:長方體的長、寬、高都變為原來的2倍,它的體積和表面積發生了怎樣的變化?學生通過計算,很快發現長方體的長、寬、高均變為原來的2倍后,長方體的表面積擴大為原來的4倍,體積擴大為原來的8倍。但教師并沒有滿足于此,而是向學生詢問:“如果將長方體的長、寬、高擴大為原來的3倍,表面積和體積會發生怎樣的變化?”學生的答案五花八門,有的說表面積是原來的6倍,體積是原來的9倍;也有的說表面積是原來的9倍,體積是原來的18倍;還有的說表面積是原來的9倍,體積是原來的27倍……面對這樣的情況,教師沒有急于告知學生正確的結果,而是引導學生從長方體的長、寬、高擴大為原來的2倍想起,列出表格:
學生在觀察表格的基礎上,,能夠說出:表面積擴大的倍數是長、寬、高擴大倍數的平方,體積擴大的倍數是長、寬、高擴大倍數的立方。教師因勢利導,提問:“可以運用含有字母的式子表示這個變化規律嗎?”學生認為如果將長方體的長、寬、高分別擴大為原來的n倍,那么它的表面積就會擴大到原來的n2倍,則體積擴大到原來的n3倍。這樣可以讓學生從表格中的數據走出來,上升到規律的角度,有助于學生得到更深層次的理解。
總之,教師應根據教學內容的特點,適時地引入表格,拓寬學生的思路,真正讓學生覺得數學不難學。
(責編黃春香)

