在實驗中促進小學數學概念建構
徐學萍

摘 ?要 著名教育學家蘇霍姆林斯基曾經說過,兒童的智慧就在他們的指尖上。在小學數學教學中也是如此,通過實驗,可以更好地幫助學生構建數學知識概念。以“軸對稱圖形的初步認識”教學為例,闡述相關的實驗教學方法。
關鍵詞 數學實驗;小學數學;軸對稱圖形;多媒體
中圖分類號:G623.5 ? ?文獻標識碼:B
文章編號:1671-489X(2019)17-0114-03
1 前言
皮亞杰認為,知識概念既不預成于內,也不預成于外,學生只有學會自主構建知識概念,知識才真正地屬于學生。數學實驗將“教”與“學”建立在“做”的基礎之上,通過直觀的實踐操作,化解知識學習的抽象之感。在“軸對稱圖形的初步認識”這節課的教學中,運用數學實驗的方式,可以更好地幫助學生構建知識概念。
2 “軸對稱圖形的初步認識”教學介紹
“軸對稱圖形的初步認識”是小學數學三年級上冊的重要知識,本節課教學要實現三個方面的教學目標[1]:
1)幫助學生感知生活中的軸對稱現象,有效地識別軸對稱圖形的基本特征,可以根據軸對稱圖形的特征,有效地識別軸對稱圖形,并且可以自主嘗試去創造軸對稱圖形;
2)從學生的生活經歷出發,從生活現象中抽象出軸對稱圖形,同時不斷地積累相關的思維活動經驗,并逐漸發展形成對空間的初步概念;
3)使學生體會軸對稱圖形在現實生活中的應用,發現數學之美,促使學生的數學學習興趣得到提升。
在“軸對稱圖形的初步認識”這節課的教學中,最大的難點是認識軸對稱圖形的基本特征,可以有效地識別平面圖形中一些簡單的軸對稱圖形圖案。在“軸對稱圖形的初步認識”這節課教學中,實驗教學方式是極為契合實用的,符合學生的認知水平和心理特點,可為學生的數學知識概念建構提供保障。
3 在實驗中促進小學數學概念建構:以“軸對稱圖形的初步認識”為例
演示實驗,發現現象 ?演示實驗是一種常見的數學實驗教學方式,可通過直觀的形象幫助學生化解數學知識學習困難,加深學生對數學知識的感受印象。在“軸對稱圖形的初步認識”教學中,教師可在課程開始之初,通過演示實驗調動學生的學習興趣,促使學生發現數學知識現象。如在演示實驗中,教師可以通過多媒體教學工具,為學生播放“小朋友玩飛機模型”的視頻:一位小朋友的飛機模型原本飛得比較平穩,并且飛得很高、很遠,但由于在飛機落地的時刻,飛機模型一側的機翼折斷了,然后就再也無法起飛了。在這樣的演示視頻播放后,教師可以向學生提出問題:“為什么小朋友的飛機模型機翼折斷后,就再也無法起飛了?”在學生思考問題的過程中,教師可以為學生出示“機翼折斷前后的飛機圖”,引導學生對比分析兩幅圖示之間的差別。此時學生就會發現,當飛機機翼一模一樣時,飛機才能飛得平穩;而當飛機機翼折斷時,飛機就不再平衡了。
教師可以帶領學生仔細觀察完好的飛機圖片,引導學生發現在飛機模型中有一條直線,沿著這一條直線,可以將飛機直接分割成兩個一模一樣的部分;然后讓學生找出這條直線到底在什么位置,直線的兩邊有怎樣的特點。通過這樣的演示實驗,引出“軸對稱圖形”的概念。教師還可以為學生展示圖1所示圖形,幫助學生認識到和飛機一樣具有軸對稱特性的圖形還有很多,如蝴蝶、天壇、五角星都是軸對稱圖形;但是最后的衣服圖形下擺一邊長一邊短,所以是不對稱的。借助這些演示實驗,幫助學生發現、理解軸對稱圖形概念。
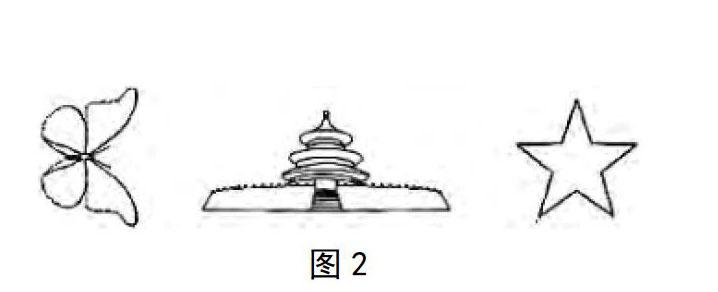
嘗試實驗,感知特征 ?在小學數學教學中,嘗試實驗為學生提供了自主操作嘗試的機會,有助于學生主體構建知識,并促使學生的思維能力得到有效培養。在“軸對稱圖形的初步認識”教學中,若是把這些對稱圖形畫出來,就可以得出圖2所示圖形。在嘗試實驗之中,教師可以引導學生大膽嘗試,想一想如果把這些軸對稱圖形剪下來,有哪些方法?最簡單的方法是什么?
如有的學生就提出沿著圖形的邊線,慢慢地將圖形剪下來;還有的學生提出,將這些圖形對折,這樣沿著圖形一半的邊形剪下來,也可以得到完整的圖形。教師可以讓學生結合自身的猜想,親自動手進行嘗試,但實際動手前可以讓學生先進行合作思考,如:“采用先對折再剪出一半圖形的方式,對折的線是任意選取的嗎?”學生通過探討嘗試就會發現,先對折,再沿一半圖形的邊線剪,是可以得到相應圖形的,但是對折的線不是任意選取的。如在蝴蝶圖形中,只有沿著兩觸角之間橫向對折,確保蝴蝶圖的上下兩邊完全相同,翅膀與翅膀、身體與身體的邊線都重合,然后進行裁剪,才能夠得出想要的蝴蝶圖形,不然是無法剪出的。而當學生嘗試用對折線剪出完全重合的圖形時,學生自然而然地就會明白什么是軸對稱圖形,并會明白能夠讓對折兩邊完全重合的線,就是軸對稱圖形的對稱軸。在嘗試實驗之中,學生可以更好地感知軸對稱圖形的特征。
驗證實驗,掌握方法 ?驗證實驗也是一種常見的數學實驗方式,通過驗證實驗,可以幫助學生解答心中的疑惑,促使學生對數學知識有更加深刻的認識感知。在“軸對稱圖形的初步認識”教學中,驗證實驗的使用主要是為了判斷“某一圖形是否為軸對稱圖形”[2]。
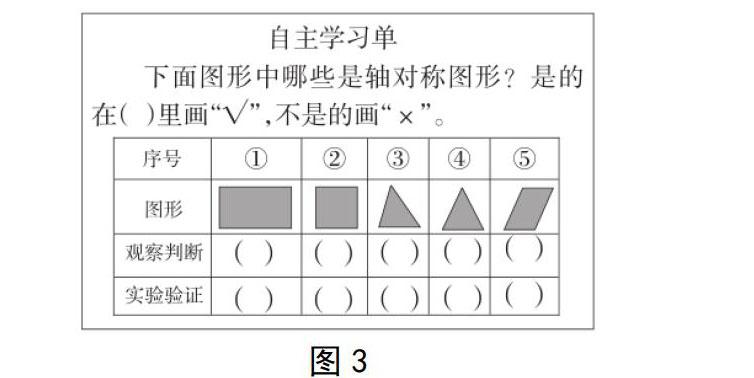
首先,判斷平面圖形是否為軸對稱圖形。如教師為學生出示圖3,讓學生判斷這些平面圖形之中哪些為軸對稱圖形。在這個過程中,教師可以讓學生思考:軸對稱圖形最主要的特征是什么?如有的學生會回答:“圖形對折后,兩邊可以完全重合。”這就是重要的驗證依據,學生可以通過觀察和動手兩種方式做出實驗驗證,最后會發現①②④為軸對稱圖形,③⑤不是軸對稱圖形,它們不管如何對折,都無法得出完全重合的圖案。
其次,判斷生活圖案。教師可以為學生出示中國工商銀行標志、車輪圖案、水杯圖案等,判斷這些生活圖案是否為軸對稱圖形。讓學生先觀察,再去進行實驗驗證,并重點探討這些軸對稱圖形的對稱軸位置在哪兒,在驗證實驗過程中進一步鞏固軸對稱圖形的判斷方法,提升空間想象力。
想象實驗,深化認識 ?數學實驗本就是“做”與“思”有效融合的過程,若是可以讓學生在“做”的過程中不斷向“思”的高度提升,對學生數學學習發展無疑是有諸多裨益的,而想象實驗為學生深化認識思考提供了機會。在“軸對稱圖形的初步認識”教學中,想象實驗的組織主要包括兩個方面。
1)在變化中體驗的想象實驗。在教學過程中,教師可以為學生出示圖4所示交通標志,先讓學生判斷第一個交通標志是否為軸對稱圖形,然后將這個交通標志依次旋轉,得到右邊的三幅圖示,并讓學生判斷后面的三個圖示是否為軸對稱圖形,以此讓學生說說自己的發現。這就是一種想象實驗的方式。通過實驗,學生會發現,軸對稱圖形無論做出怎樣的旋轉,都不會改變其為軸對稱圖形的本質事實。
2)從不同角度觀察對稱物體的想象實驗。教師可以為學生出示一個生活模型圖片,以飛機模型圖示為例,引導學生想象從前、后、左、右四個方向觀察這一飛機模型圖片,并想象判斷自己看見的圖形是否是軸對稱圖形。而在這樣的想象實驗中,學生又會有新的發現,那就是立體模型中軸對稱的物體從不同的角度觀察并畫到平面上,可能得到軸對稱圖形,也可能得到非軸對稱圖形。
在這樣的想象實驗教學中,學生對軸對稱圖形的認識不會停留在簡單的判斷上,會發現軸對稱圖形的對稱性不會隨它的位置改變而發生改變,但是通過不同角度去觀察同一軸對稱物體,看到的形狀是可能發生改變的。在想象實驗中幫助學生理清對稱現象與軸對稱圖形之間的辯證關系,深化學生對軸對稱圖形知識的認識。
操作實驗,構建知識 ?在“軸對稱圖形的初步認識”教學中涉及的操作實驗有很多,包括拼擺實驗、折紙實驗等,通過這些動手操作實驗,可以幫助學生更加全面地構建數學知識。
1)拼擺實驗,凸顯本質屬性。小學數學知識具有一定的抽象性,而學生又缺乏理性認識,因此學起來往往非常困難。在“軸對稱圖形的初步認識”教學中,教師可以通過設計拼擺實驗的方式,幫助學生構建知識認識。如為學生提供圖5所示圖片,讓學生通過親手拼擺的方式,猜一猜上面一排的撲克圖形是從下面一排的撲克紙牌之中的哪一張剪下來的。這樣的拼擺實驗操作方式可以幫助學生加深對軸對稱圖形的空間認識,從而清晰理解軸對稱圖形的本質屬性,為學生的主體知識構建增添動力。
2)折紙實驗,積累活動經驗。動手操作是數學實驗的基本方式,動手操作實驗可以充分地調動學生的多種感官,促使學生手腦并用,從而更進一步加深學生對數學知識的認識,促使學生的動手實驗能力得到增強。在“軸對稱圖形的初步認識”教學中,折紙實驗是一種非常適用的教學方式,如可以向學生提出這樣一個問題:“把一張紙對折兩次,剪出來會是什么樣子?”通過這樣的折紙實驗,讓學生自己嘗試設計軸對稱圖形,同時引導學生:“如果對折更多的次數,結果會怎樣呢?”這樣的實驗教學方式極具開放性。教師也可以將學生設計的作品展示出來,在激發學生學習興趣的同時,更好地幫助學生積累構建知識。
4 結語
“軸對稱圖形的初步認識”是小學階段重要的幾何知識內容,而數學實驗教學方式充分考慮到學生的心理特點和認知水平,可讓學生在動手操作過程中理解軸對稱圖形的概念,促使學生的空間概念得到發展,從而加快學生主體知識構建。總之,開展小數數學實驗教學是一種可行的方式。
參考文獻
[1]孫冬梅.借助數學實驗 促進概念教學:“軸對稱圖形的初步認識”教學實踐與思考[J].小學數學教育,2017(24):
50-51.
[2]戴文亞.在數學實驗中促進概念建構:以“軸對稱圖形的初步認識”為例[J].小學數學教育,2016(22):38-39.

