基本不等式復習課三步曲
☉江蘇省宜興市陽羨高級中學 孫 玲
基本不等式在高考中屬于C級要求,即要求學生熟練掌握,并能靈活應用.而在新授課時,如何靈活運用基本不等式解決有關問題,一直是學生的弱點與難點.因此,在基本不等式的復習課上,教師應該引導學生克服弱點與難點,并溫故知新.為此,筆者設計了基本不等式復習課三步曲,供參考與斧正.
一、引導學生梳理知識,并完成基礎訓練
作為復習課,這一步必不可少,既起到“溫故”的作用,又起到承上啟下的作用.
(一)知識梳理
1.幾個特殊的平均值
2.基本不等式
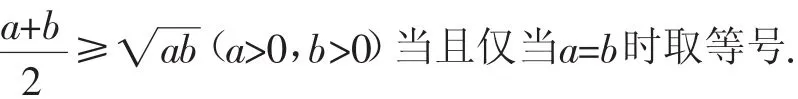
3.不等式的幾個變形
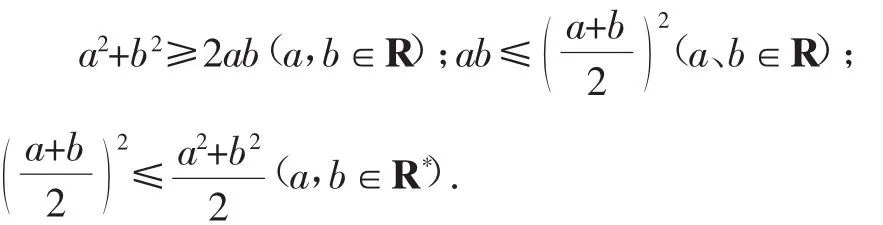
4.利用基本不等式求最值問題
已知x>0,y>0,(1)如果積xy是定值p,那么當且僅當x=y時,x+y有最小值是;(簡記:積定和最小)(2)如果和x+y是定值p,那么當且僅當x=y時,xy有最大值是(簡記:和定積最大)
應用注意點:一正,兩個未知數為正數;二定,兩個未知數的積定或和定;三相等,當且僅當兩個未知數(或整體)相等時取等號,注意定義域.
5.證明基本不等式的方法有分析法、綜合法和比較法
點評:復習課必須圍繞課題梳理知識點,梳理應做到全面且重要,應提取課本精華并加以深化.如果用不等式鏈來高度概括a+b,ab,a2+b2三個量之間的不等關系會更加簡潔明了.
(二)基礎訓練
1.已知a,b∈R,a+b=1,則a2+b2的最小值為______.
4.用長為4a鐵絲圍成一個矩形,則矩形的面積最大值是______.
5.下列函數中,最小值是4的有______個.
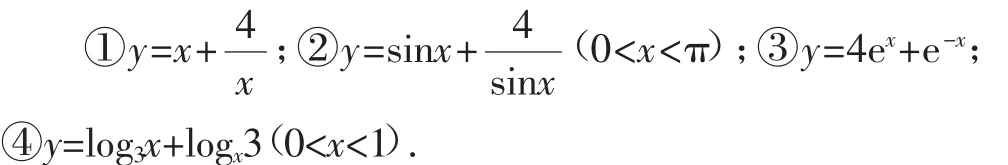
點評:以上題目涵蓋了基本不等式的簡單運用、實際應用和運用基本不等式求最值時的條件,達到了夯實基本概念和基本知識的目的,而且大部分學生都能順利解決.
二、通過例題引導學生進一步明確并掌握基本不等式的應用
例題講解一直是復習課的主旋律,因此例題的選擇十分重要,因為它是引導學生掌握知識并形成能力的載體,所以例題的選擇必須典型,同時要注意進行適當變式,以培養學生思維的靈活性.
1.證明不等式
例1(1)已知a,b,c均為實數,求證:a2+b2+c2≥ab+bc+ac;
變式1:已知a,b,c是不全相等的正數,求證
變式2:已知a,b,c是不全相等的正數,求證:lg
變式3:已知a>b>c,求證
點評:學會從不等式的特征分析,巧用基本不等式進行不等式的證明.注意輪換對稱式的識別,并應用疊加或疊乘法解決問題,同時學會拆、湊等技巧來構建基本不等式.
2.求最值或取值范圍
例2 已知正實數a,b滿足ab=a+b+3,
(1)求a+b的最小值;(2)求ab的最小值;(3)求2a+b的取值范圍.
變式4:已知實數x,y滿足4x2+y2+xy=1,求2x+y的最大值.
點評:解決雙元代數式最值的兩條解題途徑:一是把a+b和ab看作兩個量,利用基本不等式及其變形構建不等式,通過等式消元,解不等式即可求解;二是把a、b看作兩個量,通過等式消元,構建函數關系,再利用基本不等式或函數的單調性解決問題,同時注意消元的等價性.
3.在實際問題中的應用
某村計劃建造一個室內面積為800m2的矩形蔬菜溫室.在溫室內,沿左、右兩側與后側內墻各保留1m寬的通道,沿前側內墻保留3m寬的空地.當矩形溫室的長、寬各為多少時,蔬菜的種植面積最大?最大種植面積是多少?
點評:學會根據題意列出相應的等量關系,并通過消元或構建不等式求最值.
圖1
三、引導學生了解基本不等式的高考動態
學習的目的雖然不是為了高考,但對于每一位學生來說,高考不可回避.在復習課上,教師讓學生了解基本不等式的高考命題趨勢,或高考真題回顧,能激發學生的求知欲,并能讓學生從“溫故”走向“知新”.
1.最新考綱
(1)了解基本不等式的證明過程;
(2)會用基本不等式解決簡單的最大(小)值問題.
2.高考命題趨勢
在高考中,對基本不等式的考查一般不以知識點的形式出現,而是考查它的“工具性”,即利用基本不等式解決有關最值問題與不等式問題,其常與其他知識綜合在同一考題中,以此來考查不等式應用的綜合性與靈活性.
3.高考真題
例3(2018年天津高考)已知a,b∈R,且a-3b+6=0,則的最小值為______.
解析:由a,b∈R,且a-3b+6=0得,3b=a+6,
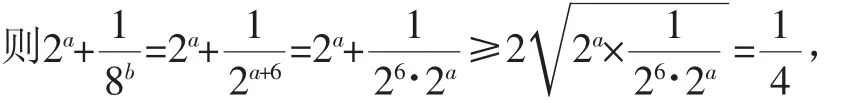
上述解法采用了代入消元法,把兩元最值問題轉化為一元最值問題,然后再利用基本不等式求最值,這是求多元最值問題最基本的方法之一.
變式5:(2018年江蘇卷)在△ABC中,角A,B,C所對的邊分別為a,b,c,∠ABC=120°,∠ABC的平分線交AC于點D,且BD=1,則4a+c的最小值為______.
解析:如圖2,因為∠ABC=120°,且BD為∠ABC的平分線,
所以∠ABD=∠CBD=60°.
又因為角A,B,C所對的邊分別為a,b,c,且BD=1,
由S△ABC=S△BDC+S△ABD得,
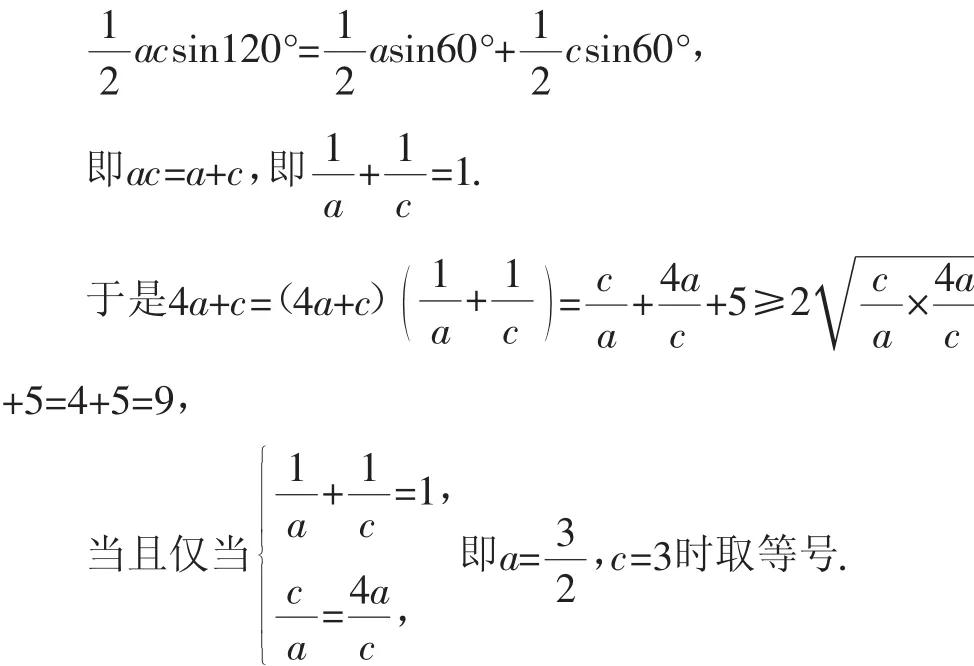
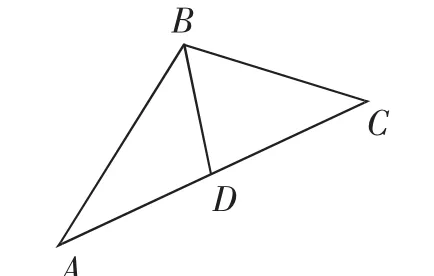
圖2
故答案為:9.
點評:高考真題體現了高考命題的方向,不僅可以讓學生感受基本不等式的高考要求,又能感受基本不等式應用中體現的數學思想,進而從高考的角度去理解基本不等式.
常言道:學無定法,教無定法.但有規律可循.筆者認為復習課也應遵循學生的認知規律,尤其是在高考的一

