小學數(shù)學雞兔同籠問題的解法探析

楊繼紅

摘? 要：雞兔同籠，是中國古代著名典型趣題之一，記載于《孫子算經(jīng)》之中。通過分析雞兔同籠問題的不同解法的具體過程，幫助學生從多方面理解雞兔同籠問題的解題策略，在合作探究中培養(yǎng)數(shù)學思維能力，滿足學生追求個性發(fā)展的需求。

關(guān)鍵詞：小學數(shù)學;雞兔同籠;解法探析;分層次教學

一、引言

“雞兔同籠”是我國古算書《孫子算經(jīng)》中著名的數(shù)學問題，其內(nèi)容是：“今有雉、兔同籠，上有三十五頭，下有九十四足。問雉兔各幾何。”意思是：有若干只雞和兔在同個籠子里，從上面數(shù)，有三十五個頭;從下面數(shù)，有九十四只腳。求籠中各有幾只雞和兔？

這就是雞兔同籠問題，此題出現(xiàn)在北師大版五年級數(shù)學上冊數(shù)學好玩板塊中，本文將從教師通過層次化教學培養(yǎng)學生數(shù)學思維能力的角度出發(fā)，梳理雞兔同籠的不同解法，引導學生結(jié)合自身學習情況選擇不同的解題方法，滿足不同層次學生學習的需求。

二、雞兔同籠問題的解法探析

例題：雞兔同籠，有9個頭，26條腿。雞、兔各有多少只？（以下所有的解法探析都是建立在此例題的基礎(chǔ)上。）

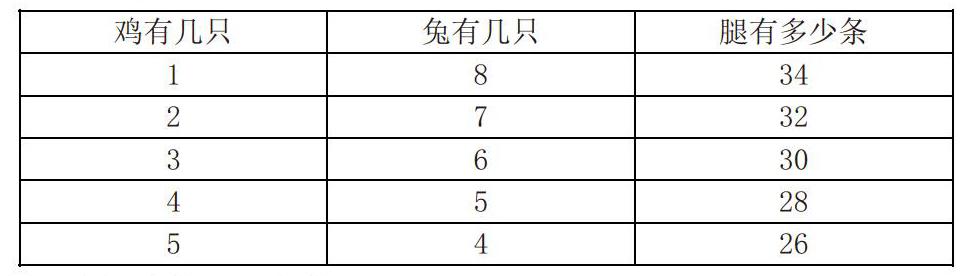
解法一：列表枚舉法。

題目中雞和兔的只數(shù)都不確定，只給出了雞和兔的總頭數(shù)和總腿數(shù)，考慮到每只雞和兔的腿并不相同，所以選擇從雞和兔的頭數(shù)也就是只數(shù)入手會容易些。考慮到雞和兔的總頭數(shù)數(shù)值上不是很大，可以進行一一枚舉。

答：雞有5只，兔有4只。

解法二：假設(shè)法。

題目中雞和兔的只數(shù)被限定在0～9之間（包括0和9），我們可以假設(shè)其中一種動物如雞有9只，此時兔有0只，然后把得到腳數(shù)與題目中的腳數(shù)進行比較，計算出兩則的差。此時計算得出實際有腿18條，比題目中雞和兔的總腿數(shù)少了8條。仔細探究后發(fā)現(xiàn)雞和兔總腿數(shù)少的原因是因為把兔當作了雞來計算，因為一只雞比一只兔少了2條腿，也就是說如果我們把一只兔當作一只雞來計算時實際計算出的雞和兔的總腿數(shù)就會少2條。此時用所得的腳數(shù)差除以2所得結(jié)果就是把幾只兔當作了雞來計算，也便得出兔的只數(shù)。用雞和兔的總只數(shù)減去兔的只數(shù)進而求出雞的只數(shù)。

[9×2=18]（條）? ? [26-18=8]（條）

[8÷2=4]（只）? ? ? [9-4=5]（只）

答：雞有5只，兔有4只。

三、砍腳法

因為雞和兔各自的只數(shù)不確定，所以從雞和兔的總腿數(shù)的角度難以解題。但一只雞有2條腿，一只兔有4條腿是確定的，可以嘗試從雞和兔的條數(shù)入手解題。如果我們砍去每只雞和每只兔的2條腿，所以雞的腿都被砍去了，而剩下的腿都是兔子的腿，并且此時每只兔子只有2條腿。用剩余腿數(shù)除以2便得到兔子的只數(shù)，再用雞和兔的總只數(shù)減去兔的只數(shù)就可以算出雞的只數(shù)。

[9×2=18]（條）? ? [26-18=8]（條）

[8÷2=4]（只）? ? ? [9-4=5] （只）

答：雞有5只，兔有4只。

四、簡易方程法

應(yīng)用一元一次方程解題時需要從實際問題中尋找等量關(guān)系，抽象成一元一次方程可解決的問題。題目中告訴我們雞和兔共有9個頭，也就是雞和兔一共有9只，此時我們可以利用雞和兔的只數(shù)的角度來設(shè)未知數(shù)，分別計算出雞和兔的腿數(shù)，根據(jù)雞和腿的總腿數(shù)為26條列出等量關(guān)系。假設(shè)雞有[x]只，那么兔的只數(shù)就是[9-x]只，根據(jù)每只雞有2條腿，每只兔有4條腿，雞的總腿數(shù)[2x]加上兔的總腿數(shù)[4×（9-x）]等于總腿數(shù)26。

解：設(shè)雞有[x]只，兔有[9-x]只。

[2x+4×（9-x）=26]

[2x+36-4x=26]

[36-26=4x-2x]

[2x=10]

[x=5]

[9-4=5] （只）

答：雞有5只，兔有4只。

五、雞兔同籠問題分層次學法指導

“為了每一個學生的發(fā)展”是基礎(chǔ)教育課程改革的核心，但是在小學數(shù)學教學過程中，學生的差異性是實實在在存在的。小學數(shù)學教師可以通過對學生的觀察、測試、摸底依據(jù)學生的成績、認知能力、心理素質(zhì)、學習習慣等，把學生大體分為A、B、C三層。A層的基礎(chǔ)相對比較扎實，學習成績優(yōu)良。B類的基礎(chǔ)水平一般。C層的基礎(chǔ)相對落后。

列表枚舉法需要將可能存在的情況一一枚舉，填寫在表格中，這類方法雖然過程有些繁瑣但簡單易懂。當數(shù)據(jù)比較小時運用此方法就比較形象直觀，易于理解，當數(shù)據(jù)較大時就會增加計算的難度，使問題變得繁瑣復雜。結(jié)合C層學生基礎(chǔ)薄弱，抽象思維和理解能力不強易于接受直觀性知識的特點，教師在教學中可適當引導采用此類方法解題。

使用一元一次方程解題需要在實際問題中尋找等量關(guān)系且熟悉解方程的步驟，這種方法較列表枚舉法雖然便捷但同時對學生的認知能力提出了更高的要求。砍腿法雖然算式看上去比較簡便，但也需要學生有豐富的生活閱歷和較強的理解能力為基礎(chǔ)，B層學生能夠掌握基本知識和一定學習方法，對方程解題也熟悉，教師在教學中可引導他們采用這兩類方法解題。

假設(shè)法適合解決雞兔同籠問題的各種題型但因為其比較抽象難以理解，所以對邏輯思維要求比較高，結(jié)合A層學生基礎(chǔ)比較扎實，思維靈活，理解能力強且學習習慣好，愛專研的特點，教師可引導此類學生采用假設(shè)法解題。

我們不可能用一把尺子去量時間萬物，同樣我們不能用同樣的標準去衡量不同的學生。每個學生雖說都不是完美的但都有著自己特有的閃光點，小學數(shù)學教師應(yīng)用欣賞的眼光看待每位學生，在日常的教學中以生為本，從學生的學習效果來中不斷改進教學方法，指導學生找到適合他們自己的學習方法，為學生的發(fā)展奠基。

參考文獻

[1]吳玉花.小學數(shù)學雞兔同籠問題的教學分析[J].新課程（小學），2016（12）.

[2]李樹清.“雞兔同籠”問題的解法探討[J].教育實踐與研究（小學），2009（03）.

[3]王素清.改進小學數(shù)學分層次教學的建議[J].中國校外教育，2015（18）.