發展元認知能力深化數學理解培育核心素養

呂同林

摘 ? ?要：學習者的元認知水平和能力是影響其深度理解數學知識結構、領悟數學思想方法、探究問題解決策略以及發展數學思維的重要因素.從教學過程來看，元認知能力的培養經歷從“扶”到“放”、從“他控”到“自控”、從“外化”到“內化”的過程;從育人目標來看，教學活動關注元認知能力的培養，有利于學習者提升思維品質、深化數學理解、形成數學核心素養;從教學實踐來看，元認知的能力培養可側重以下幾個方面：突出關聯策略，優化學習品質;強化反思行為，促進深度思考;關注主體意識，培育核心素養.

關鍵詞：元認知;數學理解;核心素養

培養學生的核心素養是當前教育的重要目標.筆者在教學實踐中體會到，數學核心素養的形成，離不開學習者的認知水平和認知能力.而學習者的元認知水平和能力是影響其深度理解數學知識結構、領悟數學思想方法、有效探究問題解決策略以及發展數學思維的重要因素.

一、元認知內涵

元認知是由美國兒童心理學家弗拉威爾（J. H. Flavell）首先提出的.他把元認知界定為反映或調節認知活動的任一方面的知識或認知活動.具體地說，就是關于個人自己認知過程的知識和調節這些過程的能力，即是對思維和學習活動的知識和控制，是對思維活動的自我體驗、自我觀察、自我監控和自我調節.元認知（也稱自我認知）就是對認知的認知，是學習者認知心理和認知策略進一步完善的過程，是完成有效認知活動的關鍵.從認知的對象看，認知的主體是知識，而元認知的主體是認知行為本身.從認知的形式看，元認知是一種高級的認知活動，是對學習活動的控制和調節.主要包括三個層面：一是元認知知識（通過學習和體驗積累起來的，關于認知的陳述性知識和程序性知識）;二是元認知監控（認知活動中，目標、計劃、實施步驟的明確，應用策略選擇，結果預測;評價活動及時反饋，方法、策略和目標及時修正調整;評價策略的使用效果以及完成任務的程度;活動結束后對結果的檢驗，后續行動方案或措施的改進）;三是元認知體驗（認知活動中產生的認知體驗和情感體驗）.研究表明：元認知也指反思自己表現的能力……如果兒童對自己的學習能力缺乏洞察，幾乎不能期望他們制定計劃或做出有效的自我調節.

因此，在數學教學過程中，教師要引領學習者基于自身認知特點，結合具體學習內容和目標，及時思考并預見學習途徑，改進并優化學習的方法和策略，反思學習過程，自我監控、調節學習進程和方法，在觀察、實驗、分析、比較、猜想、論證、反思等環節，經歷數學概念、法則、公式、性質等知識的形成過程，建構認知、思考策略，領悟知識的本質內涵，掌握數學思想方法，完善學習方略，提升思維品質.此種做法其實就是發展元認知能力的有效途徑.

二、元認知實踐

（一）教學內容：《圓周角》（九年級）

內容解析：從知識角度來看，本節課有三方面學習內容.一是圓周角的概念;二是圓周角定理及其證明;三是定理的應用.它是繼圓及其相關概念、圓心角定理、垂徑定理后的又一重要內容.深入理解圓周角概念、定理和推論為后續學習圓內接三角形、四邊形以及圓內相關量的計算、關系的論證等奠定堅實的基礎.從數學思想方法來看，定理內容探索體現了“特殊到一般”思考路徑，定理的證明突出了分類討論的數學方法，體現“特殊到一般”“一般到特殊”以及“化未知為已知”的化歸策略.從學習策略來看，圓周角概念的形成過程，由頂點位置、弧的大小變化感受運動變化的意義和價值;圓周角定理的探索與圓心角、弧等元素進行關聯，這種基于聯系的探索活動讓學生的思考深刻而靈動，并指向知識的內核;定理證明的多樣化轉化策略有助于學習者自我控制、自我調節能力的發展，并促進元認知水平的攀升.

（二）教學目標

（1）經歷圓周角概念的形成過程，體驗抽象、概括、精練的數學過程.

（2）與圓心角的性質聯系，探索圓周角的性質，感受類比遷移的數學方法，提升認知水平.

（3）探索圓周角定理的證明，感悟特殊到一般、一般到特殊、未知到已知的思考、說理策略，深化思維品質，完善思維結構.

（4）參與交流互動、語言表征、作圖呈現、反思調控等活動，促進元認知水平的發展.

目標解析：基于元認知發展的課堂教學目標，不僅關注“四基”，還要聚焦元認知能力的發展.在教學活動中，既關注知識理解程度，又關注知識理解的方式和策略，不斷強化元認知的訓練，調節和修正認知的策略，逐步深化數學理解，不斷提升思維品質.

（三）教學過程

1.關注聯系，學習新知

板塊1 圓周角概念探討

問題一 ? ①前面學習了與圓有關的哪種角？它是如何定義的？圓心角的關聯要素是什么？

②如圖1，B，C是⊙O上的兩點，畫出[BC]所對的圓心角.思考：[BC]所對角的頂點還可以在哪些位置？畫圖說明.

③能否選擇適當標準，對所畫的角進行分類？試著給這幾類角起個合適的名稱.試著給這幾類角下個定義.

評析 ? 問題①回顧已有知識，關注圓心角的定義方式以及其所關聯的量.問題②關注作圖，形成圖形表征意識，并對所畫圖形相互補充完善.問題③學生的初始表征不一定標準、規范和完美，但在思維的碰撞中，呈現思考過程，說明道理和緣由，對思考和策略調控具有積極的意義和價值.這里從已有認知出發，通過角的頂點位置變化，感受角與圓的關聯性.通過概念辨析深化圓周角認識，形成合理的認知.在概念的形成過程中，通過直觀感知、合情表達、優化和調控認知的過程，進一步發展元認知能力.

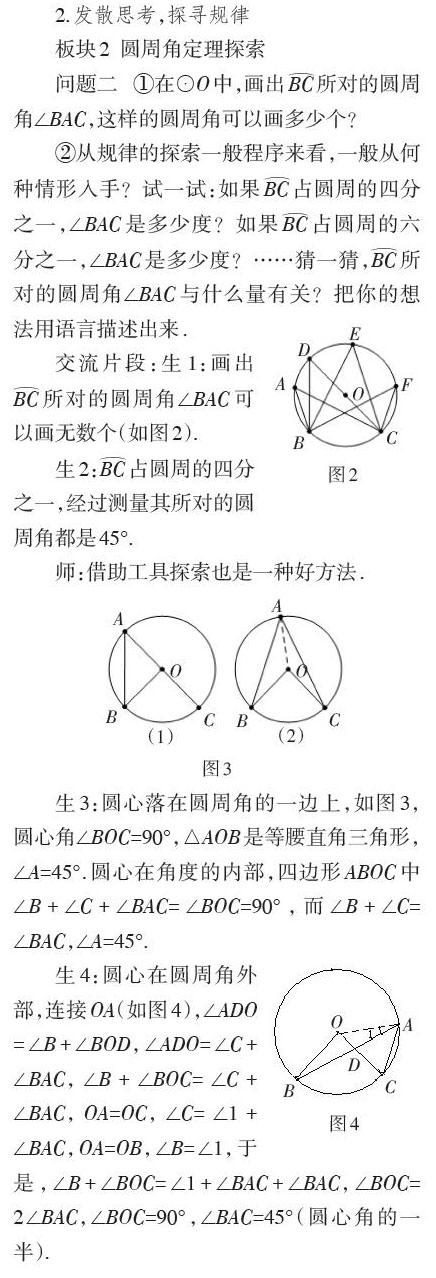
生5：從剛才的研討活動得出，[BC]占圓周的四分之一，其所對的圓周角等于45°（圓心角的一半）.

……

師：剛才，幾位同學用不同的方式，從不同的角度，探索問題解決的策略，值得我們學習.探索問題的解決方案，要緊扣已知條件和結論，分析它們之間的聯系，選擇適當方法，架設橋梁，實現從已知到未知之間的轉化.

評析 ? 經歷具體到抽象、特殊到一般的數學規律的探索過程;運用觀察、實驗、分類、歸納、猜想、計算、驗證等方法揭示數學聯系和規律，把握數學本質屬性;在自我判斷、自我選擇、自我調控等活動中，提升認知水平，發展元認知能力，提升數學思辨能力，形成數學素養.

3.反思研討，優化策略

板塊3 ?圓周角定理證明（略）

圓周角定理的證明過程中有三個重要環節：一是分類別畫圖;二是分類別證明;三是圓周角所對的弧類別的研討.定理中的圖形為什么分三類？每一類畫怎樣的圖形？證明過程是各自獨立，還是相互聯系？轉化過程中，哪種先證？其他情況向哪個方向轉化？如何轉化？圓周角所對的弧又有哪些類別？其他情形，結論是否成立？如何證明？三類弧之間以哪一類為代表較為適當？等等，無不包含豐富的元認知能力.教學活動聚焦監察、預見、控制、調節、評價等元認知要素，適當引導，及時體驗，逐步實現“他控”到“自控”、“外化”向“內化”的轉變，讓元認知發展貫穿于學習的過程，完善思維品質，提升數學素養.

三、實踐感悟

心理學認為，人的認知水平決定了思維層次，元認知的能力決定了思維的高度.我們倡導：數學教學活動，關注認知途徑、優化學習策略、調控學習過程、發展元認知能力，以此完善思考路徑、提升思維品質、深化數學理解.從實踐來看，元認知能力的培養要著力關注以下幾個方面.

（一）突出關聯策略，優化學習品質

元認知的核心是對自己的認知行為實施監控和調整.如何監控、向什么方向調整都需要學習者儲藏一定的知識、方法以及多維度、多層次分析問題、解決問題的策略.數學具有較強的整體性、聯系性、層次性、邏輯性、抽象性等特征.知識之間、結構之間、方法之間、表征形式等方面都存在一定的關聯性.在教學活動中，適時引導學生開展關聯活動，豐富思考策略，積累思維經驗，建構調控所需的資源庫.

與生活現象關聯，經歷觀察、分析、抽象、類比、猜想、歸納、驗證等活動，生成數學概念，發現數學規律，建構數學模型，形成數學原理;與前置關聯，逐步推演，厘清數學生長脈絡，形成數學思考鏈條;與相似結構關聯，明晰異同，形成新的結構圖式;關注多元表征，形成多維理解，讓思考靈動自然.“這個內容，讓我想起什么？”“此特點與哪個規律相像？”“這一內容還可以通過什么形式表達？”“回到基本概念（原點）去思考有什么發現？”……經歷這些思考，不斷監察、體驗、調控認知行為，逐步從“他控”走向“自控”，改進學習行為，豐富學習策略，完善學習品質.

（二）經歷反思活動，促進深度思考

波利亞注重解題后的“回顧”——反思環節.“你能否檢驗這個結論？”“你能否用別的方法導出這個結果？”“你能不能將這個結果或方法用于其他問題？”這是策略優化調控重要一環;“你能不能一下子看出問題的解？”這是培養解題者的“題感”，實際是對問題的敏感，是一種解題元認知的體驗.心理學的基本研究方法：“內省”即自我觀察法，它是元認知能力培養的重要策略.

學習活動中的反思行為，不能僅僅局限于解題活動.數學概念的形成、公式規律的歸納、問題的分析和解決、轉化類比策略思考等一切數學活動，凡涉及元認知活動的方面都應自覺地進行“內省”.“這樣的過程合理嗎？”“有無其他策略？”“哪種方法簡便易行？”“能否換一種方式表述？”“這樣的探索路徑是否可以用于其他問題的探索？”“其與相似內容有哪些不同之處？”“應用環節要注意什么？”“運用它可以解決哪些問題？”……教學活動不斷引領反思行為，從內容到方法、從如何思到思的全面性、從方法的合理性到結論的完備性等方面逐步發展批判性思維能力.由“他化”逐步走向“內化”，促進探索活動的深入，深化數學思考，持續提升元認知的發展水平.

（三）關注主體意識，培植核心素養

元認知水平是學習者對自身認知的反思和調整能力.初中學生元認知能力的培養需要堅持不懈地進行訓練，尤其要突出學習者主體參與意識的培養.由“扶”到“放”，通過教者的“外化提示”、學生的“出聲思維”“自我提示”等訓練活動，逐步走向行動的自覺.多關注“為什么？”“怎么辦？”“為什么這樣辦？”“怎樣辦最佳？”等思維活動，逐步引領學習者獨立分析、探索、實踐、質疑、創造，適時監察、調控認知行為，深化數學理解.營造交流互動氛圍，相互學習，相互促進，自我糾錯，自我改進;積極鼓勵策略的多樣化、個性化，激活創新潛質.

蘇霍姆林斯基說過：“我要關注的是，讓我所培育的每一個孩子都成長為會思考、會探索的有智慧的人，讓認識過程的每一步都使心靈變得更高尚，使意志煉得更堅強.”“立德樹人”是教育的根本任務.數學教師應在整個數學學習過程中，引導學習者關注學習狀態，突出活動策略，調控認知過程，經歷元認知體驗，以此促進學習者“用數學的眼光觀察世界，用數學的思維分析世界，用數學的語言表達世界”良好品質的形成.