當“發現”升級為“驗證”

王慶菊

[摘 要]在學習“三角形的內角和”之前，很多學生都已經知道了“三角形的內角和是180°”這一結論，順學而教，課堂教學的重心必然從“發現規律”升級為“驗證結論”——讓學生經歷三角形的內角和之所以為180°的探究過程，讓數學學習在建構中走向豐盈和深刻。

[關鍵詞]理性思維;推理;深度建構;三角形的內角和

【教學內容】

人教版教材四年級下冊第67頁“三角形的內角和”。

【課前慎思】

1. 四年級學生大多數都知道“三角形的內角和是180°”這個結論，而且對此深信不疑，并沒有太強的探究欲望。因此，即使教師讓學生用量角器量或用剪拼角等方法驗證這個結論，也是徒有形式的“虛假”操作。那么，本節課的生長點和核心是什么？

2.“內角”指“在封閉折線構成的圖形內的夾角”。既然是研究三角形的內角和，“內角”自然成為繞不過的概念，而教材對于“內角”概念卻只字未提。那么，需要專門進行“內角”概念教學嗎？

3.用測量法、剪拼法、折拼法等研究三角形的內角和往往不能正好得到180°。對此，能否用“誤差”一詞以概之？

4. 數學之美在于理性思維，來不得一絲“差不多”。那么，是否有嚴密的適合學生驗證“三角形的內角和”的方法，以幫助學生實現概念的深度建構？

【教學實踐】

一、直觀感知，認識內角、內角和

1. 初識內角、內角和

師（出示一個三角形，如右圖）：這是一個什么圖形？

生（齊）：三角形。

師：為什么叫三角形？

生1：因為它有三個角。

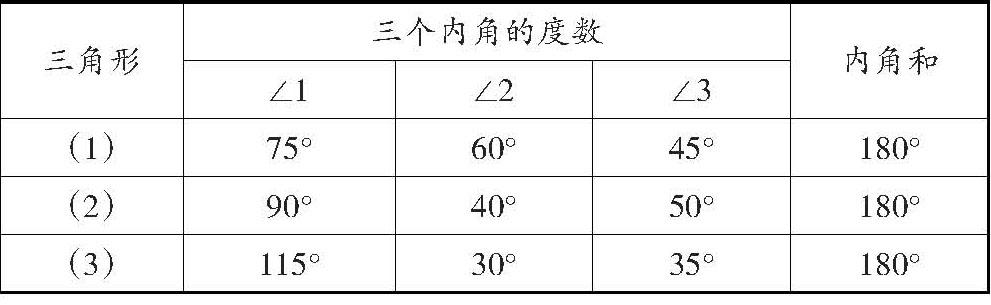
師：三角形的三個角∠1、∠2、∠3都在三角形的內部，我們可以叫它們什么角？

生2：內角。

師：把這三個內角的度數合起來，又叫什么？

生3：內角和。

2. 初識三角形的內角和

師：聽說過三角形的內角和嗎？誰能介紹自己了解到的有關三角形內角和的知識？

生4：三角形的內角和是180°。

師：你是怎么知道的？

生4：我是在書上看到的。

師：哪些同學真正研究過三角形的內角和？三角形的內角和真的是180°嗎？

二、小組交流，實踐驗證

師：你準備用什么方法研究？請先想一想，然后在小組里交流，再選擇合適的材料以小組為單位進行驗證。小組合作要求：（1）利用學具袋中提供的（或自己設計的）材料，選擇自己最喜歡的方法進行驗證，并填好記錄單。（2）通過驗證，看看可以得出什么結論。

師：現在我們召開研究成果發布會。發言的小組選一名同學當主發言人，其他同學可以補充，下面的同學當小記者，隨時準備提問。看哪個發言人表現最棒，哪個小記者最會提問題。

（1）度量法

生1：我們小組用的是測量的方法。先用量角器測量出三角形三個內角的度數，再算內角和，發現三角形的內角和正好是180°。其他同學有問題嗎？

師：這的確是個好方法。其他小組測量的結果也是180°嗎？好像有些同學遇到了一些問題。

生2：我們小組測量后發現，有的三角形的內角和是182°。

生3：我們小組測量的三角形的內角和是179°，也不是180°。

師：剛才大家都認為三角形的內角和是180°，但測量的結果有的是180°，有的不是180°。為什么會出現不同的結果？

生4：是不是量錯了？

生5：可能量角器不準。

生6：可能沒有把量角器放好。

師：的確，由于受測量工具或測量方法的影響，測量時只要有一點偏差，就會出現誤差。數學需要嚴謹，還有別的方法嗎？

（2）剪拼法

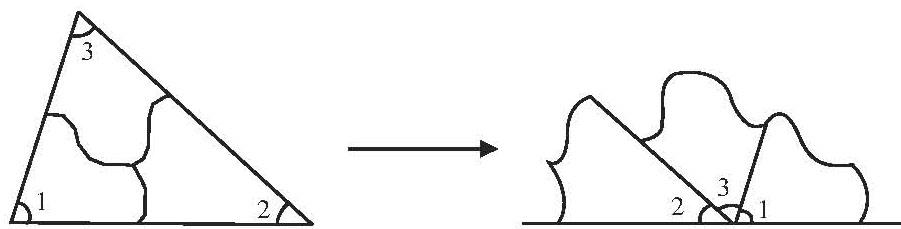
生7：我們小組用的是剪拼的方法。因為一個平角是180°，我們就想，如果三角形的三個內角剛好能拼成一個平角，不就能說明三角形的內角和是180°了嗎？于是我們把三角形的三個角撕下來拼到一起，發現正好拼成一個平角，說明三角形的內角和是180°。

師：這個小組通過變換位置，把原本不在一起的三個角轉化成一個平角。其他同學有問題要問嗎？

生8：我覺得這種方法也不太準確——拼成的角和角之間也會有縫隙，不能確定正好是180°吧？

師：的確，這種方法也會產生一定的誤差。剛才同學們分別用測量和剪拼的方法進行了檢驗，卻發現三角形的三個內角的度數和未必正好是180°。

三、以疑促思，補充完善

師：學具袋里好像還有一個材料被大家忽略了。看看是哪個圖形？

生1：長方形。

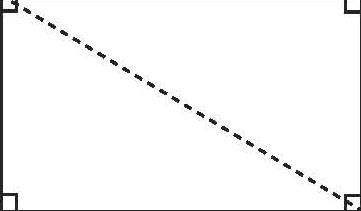
師：今天研究的是三角形的內角和。猜猜看，老師為什么要給大家準備這樣一個長方形？

生1：這個長方形沿對角線剪開后可以得到兩個完全一樣的直角三角形。長方形的每個角都是90°，4個角一共360°，所以一個直角三角形的內角和就是180°。

師：這種方法好不好？好在哪里？

生2：好！這種方法避免了在剪拼過程中出現的誤差。

生3：這種方法能說明直角三角形的內角和一定是180°。

師：是這樣嗎？這種方法實際上就是借助已知的準確數據——長方形的內角和是360°，推出直角三角形的內角和一定是180°。那么，現在可以說三角形的內角和是180°嗎？

生4：不行。銳角三角形、鈍角三角形的內角和還沒有證明呢。

師：每個同學手中都有銳角三角形和鈍角三角形，有沒有辦法進一步確認它們的內角和也是180°呢？

生5：是不是可以把銳角三角形、鈍角三角形也轉化成長方形或者直角三角形，從而得出它們的內角和？

師：試試看！

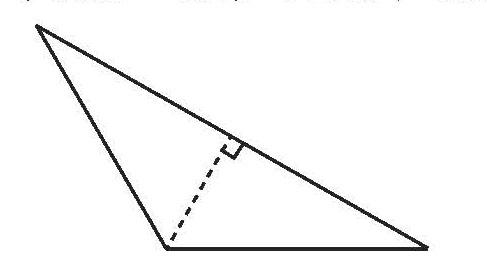
生6：在銳角三角形內畫一條高，把它分成兩個直角三角形，這兩個直角三角形的內角和一共是360°，減去增加的兩個直角的度數，那么，三角形的內角和是180°+180°-90°-90°=180°。

生7：在鈍角三角形內畫一條高，把它分成兩個直角三角形，發現每個鈍角三角形的內角和也是180°。

師：現在可以得出什么結論？

生8：所有三角形的內角和都是180°。

師：其實，早在300多年前，法國著名的數學家和物理學家帕斯卡就用這種方法驗證了任何三角形的內角和都是180°，當時他只有12歲。（介紹帕斯卡的推理證明方法）

師：為什么三角形的形狀不同，內角和卻都是180°？這里面有沒有什么奧秘？老師這里有一幅圖（用幾何畫板演示不斷變化的三角形），仔細觀察，在這個過程中，什么變了？什么沒變？你有什么發現？

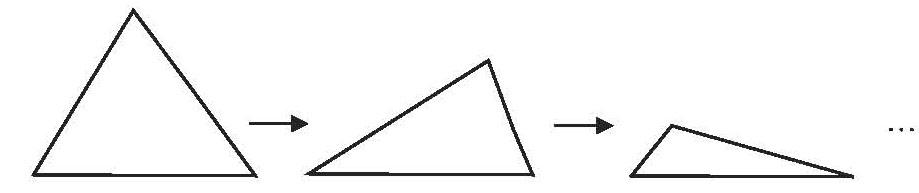
生9：三個角的度數都在變化，內角和卻總是不變。

師：如果老師把上面這個角一直往下拉，猜一猜會出現什么情況？

生10：真神奇！這個角變成了一個180°的平角，另外兩個角變成了0°，雖然這個圖形已經不再是三角形，但這三個角的和仍然是180°。

師：不同的方法，同樣的精彩！大家發現了嗎？無論是撕一撕、折一折，還是拼一拼、分一分，這些方法都有異曲同工之妙，那就是都用了轉化的策略。

四、應用感悟，豐富內涵

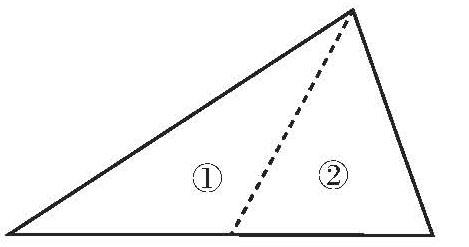
（1）一個三角形的內角和是180°，把這個三角形分成兩個小三角形，這兩個小三角形的內角和是180°嗎？

（2）把兩個三角形拼成一個大三角形，拼成的大三角形內角和是180°嗎？

（3）著名數學家陳省身爺爺在北京大學的一次講學中語驚四座：“人們常說，三角形內角和等于180°。但是，這是不對的！”這又是為什么呢？

【課后思考】

1.重要的是驗證結論

雖然很多學生在課前就知道“三角形的內角和是180°”，但對他們而言，這僅僅是一個聽來的信息而已。三角形的內角和為什么是180°，學生未必思考過。因此，本節課的教學重點不僅僅在于“三角形的內角和是多少度”，更重要的是“用什么方法來說明三角形的內角和是180°”，即讓學生通過量、撕、拼、折等方法，經歷“三角形的內角和為180°”的探究過程。正如畢達哥拉斯所言：在數學的天地里，重要的不是我們知道什么，而是我們怎么知道的。

2.在質疑中走向深刻

關于三角形的內角和，測量也好，剪拼、折拼也罷，誤差是不可避免的，許多教師對此不以為然，直接告訴學生這是誤差惹的禍。但是，用“誤差”之說解釋“三角形的內角和是180°”，是不是同樣可以解釋“三角形的內角和是179°” “三角形的內角和是182°”？如此，為什么三角形的內角和偏偏是180°？

本節課之初，當教師讓學生想辦法證明三角形的內角和是180°時，很多學生想到的就是用量角器測量三個角的度數。但測量的結果并未如他們所聽所想的那樣正好是180°。于是，有的學生開始想辦法“解決”這個問題：或調整測量結果，“湊”出180°;或先測出其中兩個角的度數，再用180°減去這兩個角的度數求出第三個角的度數，以迎合“三角形的內角和是180°”。對此，如果僅以“誤差”一詞以概之，勢必會影響學生嚴謹的科學作風和實事求是的科學精神的形成。

本節課中，從學生對“三角形的內角和是180°的深信不疑，到測量法、剪拼法的不精確，使學生對“三角形的內角和是180°”將信將疑，再到借助長方形論證以及幾何畫板演示使學生對 “三角形的內角和一定是180°”確信無疑，學生經歷了一個完整的探究發現過程，提升了思維品質，讓數學學習在質疑中走向深刻。

3.在推理中觸摸理性

中科院院士姜伯駒認為，“不講證明，數學課就失去了靈魂。其實，數學上很多概念并不是完全可以實驗出來的。比如三角形的內角相加是180°，你真用尺子去量，可能會有誤差，也許就得不到這個180°。” 數學之美在于理性思維，推理是數學思維的核心。

本節課中，當測量、剪拼等方法均不能很好地解釋三角形的內角和為什么是180°時，借助學生熟知的、顯而易見的“長方形的四個內角都是90°”“長方形的內角和是360°”這一經驗性數學事實，再結合長方形與直角三角形的內角關系，從特殊到一般進行推理，使學生真正理解了三角形的內角和之所以是180°的數學本質，同時感受轉化、變與不變的數學思想和推理力量，有效消除了直觀感知的尷尬，課堂在豐富和深刻中綻放出理性的光輝和散發出濃濃的數學味。

（責編 金 鈴）