體驗(yàn)數(shù)學(xué)文化 實(shí)現(xiàn)教學(xué)目標(biāo)

洪建龍

[摘? ?要]以“三角形的內(nèi)角和”的教學(xué)為例，先引導(dǎo)學(xué)生回顧泰勒斯的基本拼圖方法、挑戰(zhàn)泰勒斯拼圖方法，在此基礎(chǔ)上提高難度，引導(dǎo)學(xué)生繼續(xù)挑戰(zhàn)，從而讓學(xué)生自主探索與發(fā)現(xiàn)，多角度和多樣化地解決問題，實(shí)現(xiàn)知識(shí)的自我建構(gòu)，掌握科學(xué)研究的方法，形成實(shí)事求是的科學(xué)探究精神，同時(shí)感受數(shù)學(xué)文化的魅力.

[關(guān)鍵詞]數(shù)學(xué)文化;教學(xué)目標(biāo);三角形的內(nèi)角和

[中圖分類號(hào)]? ? G633.6? ? ? ? [文獻(xiàn)標(biāo)識(shí)碼]? ? A? ? ? ? [文章編號(hào)]? ? 1674-6058（2019）20-0022-02

“三角形的內(nèi)角和”是人教版教材八年級(jí)上冊(cè)第十一單元的內(nèi)容，屬于“空間與圖形”的范疇，是在學(xué)生已經(jīng)掌握了三角形的穩(wěn)定性和三角形的三邊關(guān)系相關(guān)知識(shí)后對(duì)三角形的進(jìn)一步研究，主要驗(yàn)證“三角形的內(nèi)角和等于180°.教材中安排學(xué)生對(duì)不同形狀、大小的三角形進(jìn)行度量，再讓學(xué)生運(yùn)用拼、折、剪等方法及通過觀察、猜想、實(shí)驗(yàn)、驗(yàn)證等數(shù)學(xué)活動(dòng)，探索發(fā)現(xiàn)三角形的又一特性——三角形的內(nèi)角和等于 180°.學(xué)生在探索過程中體驗(yàn)了發(fā)現(xiàn)的樂趣，發(fā)展了推理能力，感受到了數(shù)學(xué)文化的魅力，增強(qiáng)了學(xué)好數(shù)學(xué)的信心;學(xué)生在動(dòng)手獲取知識(shí)的過程中，培養(yǎng)了創(chuàng)新意識(shí)、探索精神和實(shí)踐能力.采用探究式教學(xué)，可讓學(xué)生在開放的學(xué)習(xí)過程中，自主進(jìn)行探索與發(fā)現(xiàn)，多角度和多樣化地解決問題，從而實(shí)現(xiàn)知識(shí)的自我建構(gòu)，掌握科學(xué)研究的方法，形成實(shí)事求是的科學(xué)探究精神.

一、 回顧泰勒斯的基本拼圖方法，了解定理起源

回顧泰勒斯最基本的拼圖方法，了解發(fā)現(xiàn)三角形內(nèi)角和定理的起源.

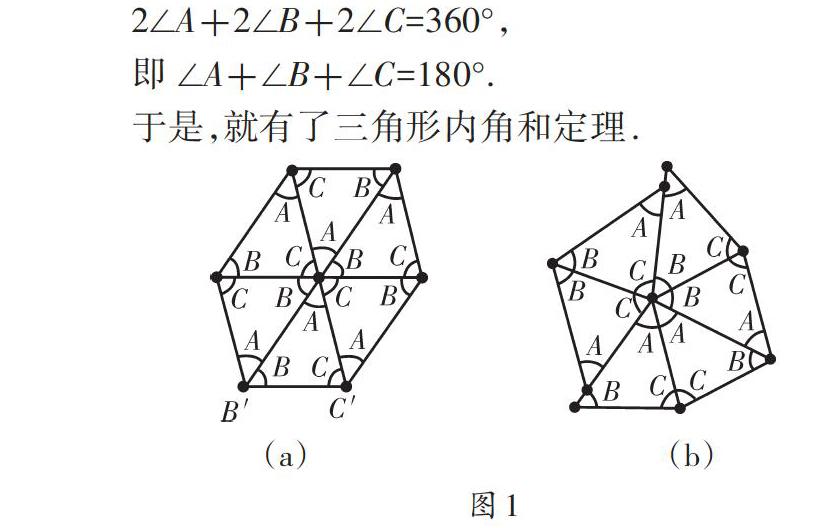
方法1：準(zhǔn)備六個(gè)全等的三角形，利用它們動(dòng)手拼圖，討論交流，得出拼圖結(jié)果.如圖1所示，三角形的內(nèi)角的頂點(diǎn)重合，并且頂角不重疊地拼在一塊，拼成一個(gè)周角（360°），三角形的每個(gè)頂角各出現(xiàn)兩次.則：

教師：大家很厲害！重新發(fā)現(xiàn)了古希臘數(shù)學(xué)家泰勒斯曾用過的方法.當(dāng)年，泰勒斯就如大家一樣，用六個(gè)全等的三角形拼圖，拼成了一個(gè)周角，從而發(fā)現(xiàn)了三角形的內(nèi)角和為180°.大家還原泰勒斯的三角形拼圖方法.真是英雄所見略同.真的了不起！

二、 挑戰(zhàn)泰勒斯拼圖方法，掌握定理

針對(duì)泰勒斯用六個(gè)全等的三角形拼圖發(fā)現(xiàn)三角形內(nèi)角和定理，教師向?qū)W生提出任務(wù)：挑戰(zhàn)泰勒斯拼圖方法.

教師：為了解釋三角形的內(nèi)角和為180°，泰勒斯用上六個(gè)全等的三角形，實(shí)在是太多了，如果用三個(gè)同樣的三角形拼圖，大家能完成嗎？

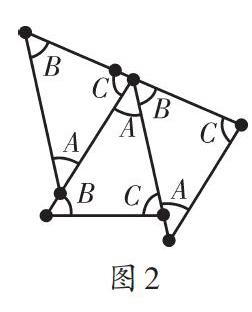
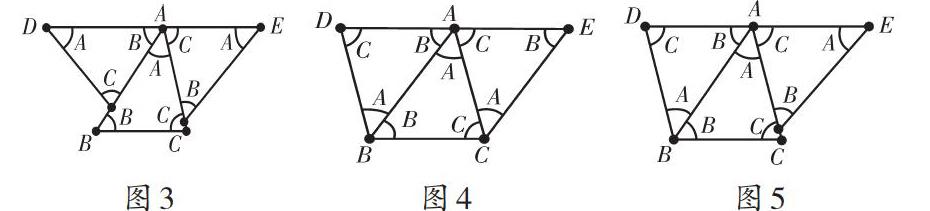
全體學(xué)生積極響應(yīng)，大家使出渾身解數(shù)，苦苦思索，嘗試拼圖.忽然，有學(xué)生發(fā)現(xiàn)，圖1（a）去掉上面一半，剩下部分表明三個(gè)同樣的三角形照樣能拼得三個(gè)內(nèi)角的和為180° .于是學(xué)生嘗試應(yīng)用三個(gè)全等的三角形進(jìn)行拼圖，如圖2、3、4、5，得出精彩的結(jié)果.教師一一展示學(xué)生的拼圖作品.

如圖2、3、4、5，三角形的內(nèi)角頂點(diǎn)重合，并且頂角不重疊地拼在一塊，拼成的圖形中，三角形的每個(gè)頂角各出現(xiàn)一次，剛好擺成一平角（180°），所以 ∠A+∠B+∠C=180°.

教師：數(shù)學(xué)家泰勒斯曾用六個(gè)全等的三角形去拼圖，而你們只用三個(gè)全等的三角形拼圖就能說明三角形內(nèi)角和定理，真是青出于藍(lán)而勝于藍(lán)！

教師要求學(xué)生繼續(xù)觀察圖2、3、4、5，思考圖3、4、5中有什么相等.

學(xué)生通過討論得出：圖形中有角相等，并且還是內(nèi)錯(cuò)角，由此得到平行線.圖3、4、5提示：過點(diǎn)A作輔助線DE平行BC，利用內(nèi)錯(cuò)角相等，從而把角B、C移到上面而構(gòu)成一個(gè)平角，不難得到三角形的內(nèi)角和定理.

教師：利用三個(gè)全等的三角形把三個(gè)內(nèi)角拼成一平角，實(shí)現(xiàn)拼圖解讀三角形內(nèi)角和為180°.我們找到的這種拼圖法，也非常簡(jiǎn)潔，它最早由古希臘數(shù)學(xué)家泰勒斯發(fā)現(xiàn).

點(diǎn)評(píng)：利用三個(gè)全等的三角形去拼圖已經(jīng)給學(xué)生機(jī)會(huì)去進(jìn)行數(shù)學(xué)創(chuàng)新，體驗(yàn)創(chuàng)新;并且還進(jìn)一步讓學(xué)生去發(fā)現(xiàn)證明三角形內(nèi)角和定理的輔助線方法，同時(shí)，也給學(xué)生作輔助線提供了一個(gè)基石，開闊了學(xué)生的眼界，豐富了三角形內(nèi)角和的內(nèi)涵.

三、提高難度，繼續(xù)挑戰(zhàn)

泰勒斯用三個(gè)全等的三角形進(jìn)行拼圖去解釋三角形內(nèi)角和定理，其實(shí)數(shù)學(xué)家帕斯卡少年時(shí)只用一個(gè)三角形就說明了三角形內(nèi)角和定理.教師利用這個(gè)案例激發(fā)學(xué)生思考的熱情，培養(yǎng)學(xué)生的數(shù)學(xué)思維，加深學(xué)生對(duì)三角形內(nèi)角和定理的理解和掌握.

教師：泰勒斯用六個(gè)或三個(gè)全等的三角形拼圖，你們能只用一個(gè)三角形說明三角形的內(nèi)角和為180°嗎？

教師的提議立即得到學(xué)生的響應(yīng)，學(xué)生紛紛思考、討論起來，有的學(xué)生說沒辦法拼圖，有的學(xué)生看到別的同學(xué)將三角形紙片折來折去，于是得到啟發(fā)：既然無法拼圖，那就進(jìn)行折紙.于是，就有了如下創(chuàng)新：

方法1：如圖6的三角形，把上面的角沿虛線橫折，使它的點(diǎn)落到底邊上，再將剩下的兩個(gè)角橫折過來，使三個(gè)角正好拼在一起，這樣三個(gè)角就組成了一個(gè)平角，所以可得出結(jié)論：三角形的內(nèi)角和是 180°.

方法2：如圖7，作三角形三個(gè)內(nèi)角的角平分線，交于一點(diǎn)O，將三角形的三個(gè)頂點(diǎn)對(duì)準(zhǔn)交點(diǎn)O折疊，折過來得到三個(gè)角A、B、C，還有三個(gè)空白部分，正是三個(gè)角∠A、∠B、∠C的對(duì)頂角，大小正好等于∠A、∠B、∠C，則有2∠A、2∠B、2∠C剛好圍成一個(gè)周角，即2∠A+2∠B+2∠C=360°，于是? ∠A+∠B+∠C=180°.

教師：大家的方法非常新穎.不過，這兩種方法，帕斯卡在12歲時(shí)早已發(fā)現(xiàn).他的父親得知他利用對(duì)稱巧妙進(jìn)行拼圖，獨(dú)立地獲得三角形內(nèi)角和定理時(shí)，激動(dòng)不已，當(dāng)即解除對(duì)他數(shù)學(xué)學(xué)習(xí)的禁令，讓他可以閱讀任何數(shù)學(xué)書籍.自然，后來帕斯卡成為法國(guó)著名的數(shù)學(xué)家、物理學(xué)家、哲學(xué)家.盡管你們是重新發(fā)現(xiàn)帕斯卡的方法，但你們也算創(chuàng)造性地運(yùn)用了這一方法，獨(dú)立地發(fā)現(xiàn)了三角形內(nèi)角和定理，非常了不起！

教師：還有別的辦法嗎？

學(xué)生又給出了方法3.

方法3：取△ABC兩邊AB、AC的中點(diǎn)D、E，如圖8，過中點(diǎn)D、E作第三邊的垂線，并沿垂線剪下，得兩個(gè)三角形，把這兩個(gè)三角形依圖形補(bǔ)上，得一正方形（如圖9）.三角形的三個(gè)內(nèi)角剛好拼成一平角.于是? ∠A+∠B+∠C=180°，說明三角形的內(nèi)角和等于180°.

點(diǎn)評(píng)：剪三角形將三個(gè)內(nèi)角拼成一平角，方法仍然巧妙，開闊了學(xué)生的視野.由三個(gè)全等的三角形拼圖到只用一個(gè)三角形，同樣能說明三角形內(nèi)角和定理，是一個(gè)大挑戰(zhàn)，但學(xué)生仍然創(chuàng)造性地解決了問題，這對(duì)于培養(yǎng)學(xué)生“直觀想象”核心素養(yǎng)、發(fā)展學(xué)生創(chuàng)新思維具有極高的價(jià)值.

四、 挑戰(zhàn)帕斯卡，不拼也不折

由六個(gè)全等的三角形、三個(gè)全等的三角形拼圖，再到只有一個(gè)三角形在拼、折中發(fā)現(xiàn)、解釋三角形內(nèi)角和定理，難度越來越大，但問題解決得越來越精彩.教師提出問題：若不折、不拼還能發(fā)現(xiàn)、解釋三角形內(nèi)角和定理嗎？比如，旋轉(zhuǎn)一支筆，能發(fā)現(xiàn)三角形內(nèi)角和定理嗎？ 許多學(xué)生感到很疑惑，用一支筆如何能說明三角形內(nèi)角和為180°？他們用筆比畫著，絞盡腦汁，師生共同關(guān)注，一起交流，最終比畫出三角形內(nèi)角和定理.

方法：如圖10，學(xué)生將BC上的筆的筆尖指向點(diǎn)C，繞B點(diǎn)沿逆時(shí)針方向旋轉(zhuǎn)角度B，與BA方向一致，筆平移到筆端與點(diǎn)A重合，繞BA上的筆尖點(diǎn)A逆時(shí)針方向旋轉(zhuǎn)角度A，與AC重合，筆平移到筆端與點(diǎn)C重合，繞此點(diǎn)C逆時(shí)針方向旋轉(zhuǎn)角度C，筆尖指向點(diǎn)B，與CB重合，與剛開始的筆尖指向點(diǎn)C比較，筆已轉(zhuǎn)過180°，恰好是三角形三內(nèi)角的和，這樣說明了三角形內(nèi)角和定理.

教師：同學(xué)們做出了德國(guó)數(shù)學(xué)家提波特的精彩作法.1809年，德國(guó)數(shù)學(xué)家提波特利用旋轉(zhuǎn)的方法證明了三角形內(nèi)角和定理.如圖10，將AB所在的直線[xy]繞A沿逆時(shí)針方向旋轉(zhuǎn)角度A，到AC所在直線[x′y′]，將[x′y′]繞點(diǎn)C沿逆時(shí)針方向旋轉(zhuǎn)角度C，到BC所在直線[x″y″]，最后[x″y″]繞B沿逆時(shí)針方向旋轉(zhuǎn)角度B，到AB所在直線[x?y?]，從[xy]到[x?y?]，總共轉(zhuǎn)過180°.

點(diǎn)評(píng)：三角形內(nèi)角和定理的發(fā)現(xiàn)、解釋，方法巧妙，精彩紛呈，只要指點(diǎn)得當(dāng)，學(xué)生就能得出同數(shù)學(xué)家一樣的創(chuàng)造性發(fā)現(xiàn).回憶數(shù)學(xué)家精彩的發(fā)現(xiàn)、巧妙的思想、經(jīng)典的定理，讓師生體驗(yàn)數(shù)學(xué)的巧妙，深刻地理解知識(shí)，感受數(shù)學(xué)文化的魅力.

新課標(biāo)注重學(xué)生三維目標(biāo)的培養(yǎng)，在這里，要求學(xué)生用自己的方法進(jìn)行驗(yàn)證，把知識(shí)的學(xué)習(xí)和情感態(tài)度與價(jià)值觀的培養(yǎng)融為一體，無疑有效地培養(yǎng)了學(xué)生的科學(xué)態(tài)度.拼圖探究是課程改革所倡導(dǎo)的一種學(xué)習(xí)方式，利于學(xué)生的創(chuàng)新意識(shí)和實(shí)踐能力的培養(yǎng)，把學(xué)習(xí)的時(shí)空還給學(xué)生，讓學(xué)生通過量、折、拼、剪、擺等操作活動(dòng)理解和掌握三角形內(nèi)角和定理，同時(shí)有效培養(yǎng)學(xué)生的發(fā)散性思維.

（特約編輯? ? 安? ?平）