練在適當處，學向深度行

王廣木

數學是一門用來表達事物空間形式與數量關系的科學，是人類思維的體操。在數學教學中，課堂練習具有重要作用，它可以幫助學生及時鞏固知識、發展智力。教師要重視課堂練習內容和形式的設計，更要重視練習出示的時機，在學生學習的關鍵處，為學生設計一定的練習活動，讓學生及時內化知識，發展能力。筆者結合教學實踐，談談如何適時地在教學中進行課堂練習，提高學生學習實效。

一、練在生長處，搭建支架

作為教師，要充分分析學情，了解學生已有的知識經驗，弄清新知學習所需的知識基礎，在學生知識生長處為學生安排課堂練習，幫助學生在舊知基礎的土壤上，主動地建構新的知識體系。如，在人教版四年級上冊“除數是整十數的筆算除法”的教學中，筆者簡單導入后，就為學生設計了如下課堂練習。

第一題：口算估算。

60÷30=2 480÷60=8

62÷30≈2 484÷60≈8

第二題：列豎式計算。

除數是兩位數的筆算除法的計算原理與除數是一位數的筆算除法相同，只是試商的難度加大了。因此，筆者在學生已有知識基礎上設計了除數是整十數的口算、估算，為學生試商做好充分的準備，設計除數是一位數的筆算除法，讓學生回顧筆算的方法，如商的位置、余數必須比除數小等知識，為學生學習新知搭建支架。學生在教師搭建的支架上學習新知，促進學生主動地、有深度地進行數學學習。

二、練在薄弱處，夯實基礎

教師要立足學生知識的薄弱處，為學生設計有針對性的課堂練習，幫助學生夯實基礎，發展技能，積累數學活動經驗，發展數學能力。如，在教學人教版小學數學四年級下冊“乘法分配律”時，筆者設計了以下課堂練習。

第一題：說一說。請你用自己的話，同桌互相說一說乘法分配律。

第二題：比一比。8×（125+7）和8×（125×7）的計算結果一樣嗎，為什么？請你算一算。

第三題：選一選。下面三個算式，正確的是（ ）。

A. 56×（19+28）=56×19+28

B. 32×（7×3）=32×7+32×3

C. 64×64+36×64=（64+36）×64

第四題：練一練。

99×14+14 101×99 25×44

小學四年級學生的觀察、比較、概括、歸納能力有限，學習了乘法分配律后，容易受到乘法結合律的負遷移，常常混淆乘法分配律和結合律，在運用上錯誤百出。于是，筆者設計了說一說、比一比、選一選、練一練四個練習活動。“說一說”是為了幫助學生識記乘法分配律;“比一比”是為了加強乘法分配律和乘法結合律的對比，避免學生混淆;“選一選”是為了深化學生對乘法分配律的理解;“練一練”是為了幫助學生靈活運用乘法分配律。這一系列的課堂練習，針對學生學習的薄弱處展開設計，有效地幫助學生鞏固知識、發展能力。

三、練在易錯處，彌補缺漏

教師為學生設計的課堂練習，要立足學生知識運用的易錯處，將學生帶進教師設置的學習“陷阱”，讓學生在練習中主動發現錯誤，思考錯誤產生的原因，探尋避免錯誤的方法，為進入更深層次的學習打好基礎，提高思維的縝密性和深刻性。如，在人教版小學數學四年級上冊“因數中間或末尾有零的筆算乘法”的教學過程中，筆者在學生易錯處設計了如下的課堂練習，幫助學生熟練掌握簡便筆算。

第一題：寫出下面的乘法算式的末尾各有幾個零。

340×70的積末尾有（ ）個零，340×50的積的末尾有（ ）個零;

125×8的積的末尾有（ ）個零，250×40的積的末尾有（ ）個零。

第二題：判斷下面的題目有錯嗎，有錯的話請改正。

第三題：筆算。

440×60 360×25 580×12

學生在三年級已經學習了因數中間有零的計算，因此學生學習重點就是掌握因數末尾有零的簡便筆算方法。由于學生受到“筆算時相同數位對齊”的思維定式的影響，多數學生在計算時出錯較多，有的學生沒有用簡便筆算，有的學生忘記在積的末尾添零，有的學生在不該出現零的地方出現了零。為了幫助學生掌握因數末尾有零的簡便筆算方法，筆者設計了以上一組課堂練習。第一題，幫助學生理解影響積末尾的零個數的因素;第二題，鞏固因數末尾有零的簡便筆算;第三題，運用因數末尾有零的簡便筆算進行計算，加深對計算方法的理解和掌握。這樣的課堂練習，在學生易錯的地方適時強化，有利于幫助學生掃清知識障礙，及時彌補缺漏，推進學生的數學學習。

四、練在提升處，強化能力

學生學習了教材知識，經歷了一定的觀察、操作等數學活動，具備了一般的數學能力。然而，學生有主動發展的需求，僅讓學生具備一般數學能力是不能滿足學生發展需求的，教師還要重視提升學生的數學能力。此時，課堂練習便可以發揮很大效用。教師通過課堂練習為學生提供了具有挑戰性的學習任務，讓學生在具體情境中嘗試解決問題，通過發散思維、集中思維等探尋解決問題的方法，在不斷嘗試中形成新的能力。如，在人教版小學數學五年級下冊“旋轉”的教學過程中，在學生認識旋轉三要素，理解圖形旋轉前后大小和形狀不變，位置改變，理解了圖形旋轉的本質特征后，如何深化學生對“旋轉”的認識，培養學生思維的靈活性，提升學生能力？筆者設計了如下題目。

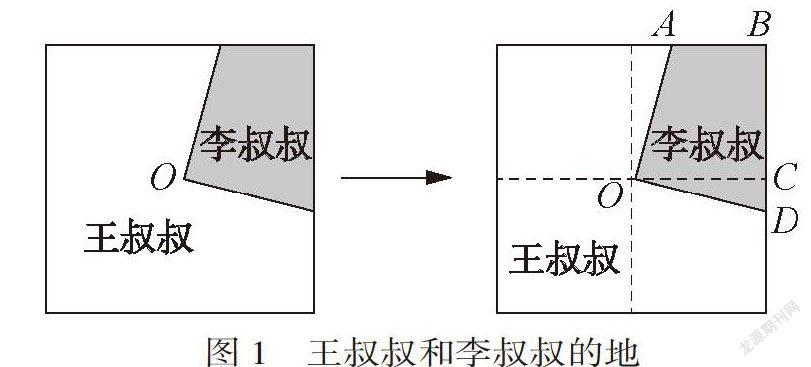
王叔叔和李叔叔共同種一塊正方形菜地（如下圖），O是正方形的中心，這兩塊地形狀都不規則，種起來很麻煩，兩人商量重新分這塊地，你知道李叔叔應分得這塊地的幾分之幾嗎？

這樣的題目，密切聯系實際，富有童趣。學生在解決問題過程中，經歷觀察、想象、操作、描述等一系列活動，數學能力得到發展提升。在解決問題過程中，學生發現，要知道李叔叔應該分得這塊地的幾分之幾，需要通過添加輔助線的方法，將李叔叔的土地進行分割，將不規則的圖形轉化成規則的圖形，再利用旋轉的知識進行解決。因此，可以將分割后的直角三角形COD繞點O逆時針旋轉90°（或者繞點O順時針旋轉270°）;或者將直角梯形AOCB繞點O順時針旋轉90°（或者繞點O逆時針旋轉270°）。在解決問題的過程中，讓學生通過觀察、想象等一系列數學活動，經歷正向思維和逆向思維的交互，運用“轉化”的數學思想方法，培養了學生的數學表達能力，提升了學生空間想象能力和問題解決能力。因此，教師要在學生能力提升處，適時設計一定的課堂練習。

本文系福建省教育科學“十三五”規劃2018年度一般課題“基于大數據的個性化校本作業實踐研究”（課題編號：FJJKXB18—397）系列成果之一。