初中數學核心素養例談
江金亮 胡淑花
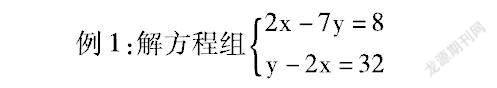
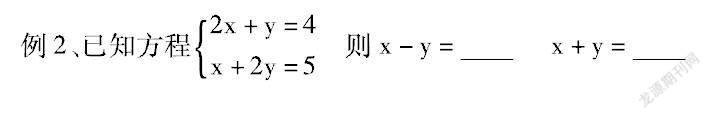
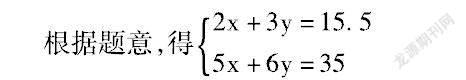

摘要:《數學課程標準(2011年版)》指出:數學思想蘊涵在數學知識形成、發展和應用的過程中,是數學知識和方法在更高層次上的抽象與概括。讓學生積極參與教學活動,通過獨立思考、合作交流,逐步感悟數學思想,積累數學活動經驗。依據課程標準,在初中數學教學中,教師要重視歸納數學思想方法,培養學生運用數學思想方法解決問題的能力,提升學生的數學素養。
關鍵詞:方程組 ????整體思想 ????核心素養
數學核心素養反映數學本質和數學思想,是數學基礎知識、基本能力、數學思考和數學態度的綜合表現,是在數學學習過程中形成的。學生在學習中準確掌握數學思想對培養數學核心素養能起到事半功倍的效果。整體思想是重要的數學思想之一,學習數學的過程中經常會遇到整體思想,如求代數式值、解方程或方程組等。所謂整體思想就是通過研究事物的整體而獲得對其局部認識的思想。在數學教學活動中,通過多次反復思考、積累,使學生認識到學會整體思想,不僅解題方法別致新穎,而且能達到迅速準確解題的目的。對于某些問題,不是從局部著手,而是從整體上觀察,探求解題途徑。下面舉例說明。
例1:解方程組
思路點撥:1、觀察兩方程中都有2x
2、將2x看作整體代入求解
技巧反思:解方程組時,首先要觀察各方程特點,運用整體代入,達到消元,求出方程組的解。
思路點撥:1、觀察兩個方程組中同一未知數的系數關系
2、發現兩個方程組相減或相加,可直接得到x-y或x+y的值
技巧反思:解答已知方程組,求代數式的值這類題時,應通過觀察、比較找出方程組與所求代數式的聯系,然后整體思維,從而求出代數式的值,避免思維定勢,先解方程組,再代入求值。加減法不僅可以消元,還可以化簡方程組直接求代數式的值,這樣省時,快速,簡便。
三、拓展思路
例3、三個同學對問題“若購買鉛筆7支,作業本3本,圓珠筆1支,共需10元,購買鉛筆10支,作業本4本,圓珠筆1支,共需12元,則購買鉛筆11支,作業本5本,圓珠筆2支,共需多少元?提出各自的想法。
甲說:“這個題目條件不夠,不能求解。”
乙說:“它們的數有一定的規律,可以試試。”
丙說:“能不能把購買鉛筆11支,作業本5本,圓珠筆2支,共需的錢數作為整體,通過整體加減的方法來解決?”
參考他們的討論,你認為這個題目的解應是________
思路點撥:觀察發現將鉛筆7支,作業本3本,圓珠筆1支,共需10元中的各數都乘以3,再減去鉛筆10支,作業本4本,圓珠筆1支,共需12元中的各數,即可直接求解。
例4、有大小兩種貨車,2輛大貨車與3輛小貨車一次可以運貨15.5噸,5輛大貨車與6輛小貨一次可以運貨35噸,3輛大貨車與5輛小貨車一次可以運貨多少噸?(人教版102頁第5題)
解法1:把3y整體代入消去y,求得x,再代入求得y,然后求得3x+5y的值
解法2:把2x+3y=15.5整體乘以7,再減去5x+6y=35得9x+15y=73.5,然后整體除以3得到3x+5y=24.5
技巧反思:通過此題鼓勵學生多角度考慮問題,從現實情境中抽象出數學問題,學會建立數學模型,從而培養學生的應用意識和運用數學思想解決問題的能力。
3、(2018嘉興)用消元法解方程組 ????????????????兩位同學的解法如下:
解法一:由①-②得3x=3
解法二:由②得3x+(x-3y)=2 ?③
把①代入③得3x+5=2
總之,在解決具體問題的過程中,如果能從數學思想的角度進行分析,可以更好地把握解題規律,達到事半功倍的效果,這正是數學核心素養數學抽象、數學建模、數學運算的具體體現。學生在反思運用數學思想解決問題的過程中,逐步學會思考,積累經驗,慢慢養成良好的學習習慣,從而提升自身的數學核心素養水平。

