關于概率統計課型的淺思考
摘 要:本文從統計學的專業角度對“2017年全國青年教師展示課”概率統計課進行論證,對概率統計課型重新思考和梳理,將模型意識、質疑式、情境教學充分融合,在此基礎上設計“普查與抽樣調查”一課,課堂呈現如下。
關鍵詞:概率統計;模型意識;質疑式;情境教學
由于初中學生認知的局限性,初中數學中的代數問題和幾何問題大都是基于理想化的生活模型培養學生的理性思維和邏輯性思維。但是由于概率與統計與實際生活聯系密切,很難將其模型化。究竟怎么教初中部分概率和統計的疑惑一直縈繞在心頭,筆者在2017年的收官之月帶著心中的疑團觀摩了“全國青年教師展示課”會議的概率專場。
概率專場的第一節課是江蘇南京三中文昌初中的陳娟老師展示蘇科版九年級上冊《等可能性》。在本節課陳老師形成的概念為:若一個數學試驗,共有n個可能的結果,它們都是隨機事件,每次試驗有且只有一個結果出現,每個結果出現的概率均等,則這個試驗的結果具有等可能性。陳老師要求學生舉出生活中等可能性的實例,經過討論學生給出如下三個例子:(1)生孩子是男還是女;(2)打開電視時正在播放電視節目還是正在播放廣告;(3)翻書翻到其中一頁。這三個例子確實出自生活,但其是否為等可能性的呢?
查閱統計專業書籍發現,等可能性出自“古典派別”,根據古典方法的基本思想:(1)所涉及的隨機現象只有有限個樣本點;(2)每個樣本點發生的可能性相等(稱為等可能性)。例如,拋一枚均勻硬幣,“出現正面”與“出現反面”的可能性相等;拋一枚均勻骰子,出現各點(1~6)的可能性相等;從一副撲克牌中任取一張,每張牌被取到的可能性相等。注意到上述三個等可能的例子中,均強調試驗用具是均勻的,所以只有理想化的模型才能實現均勻化要求。在上面例子中,孩子性別不是在出生時才隨機確定的;電視節目播放時間一般要比廣告播放時間要長;翻到中間頁碼的概率要更大一些。所以根據定義,這三個例子都不是等可能性的例子。由于統計的貼近生活性,從現實生活中抽象出等可能性的例子具有很高的難度。
概率專場的第二節課是青海海東樂都賈灣中心學校的許彩林展示《用列舉求概率(1)》,在本節課中許老師通過讓同學們拋擲兩枚一元硬幣來學習用列舉法求概率,此問題求概率的基礎在于拋擲一元硬幣時正面朝上和反面朝上的概率均為,即硬幣的正反面是均勻的。但實際上,1元硬幣正反面并不均勻,所以拿1元硬幣讓學生做試驗只能作為理想化的教具,很難得到準確答案。
研究過后,筆者設計了《普查與抽樣調查》一堂課。整節課堂基于“以學生為主題,以問題為主線,以質疑為特征”的質疑式教學模式展開,經過前期了解學情,學生的疑問集中在如下兩個問題:(1)在一個問題中如何判斷選擇普查還是抽樣調查?(2)抽樣調查中的誤差怎么避免?針對學生的第一個疑問,引申出普查的概念和抽樣調查的概念,及總體、個體、樣本、樣本容量的辨析。
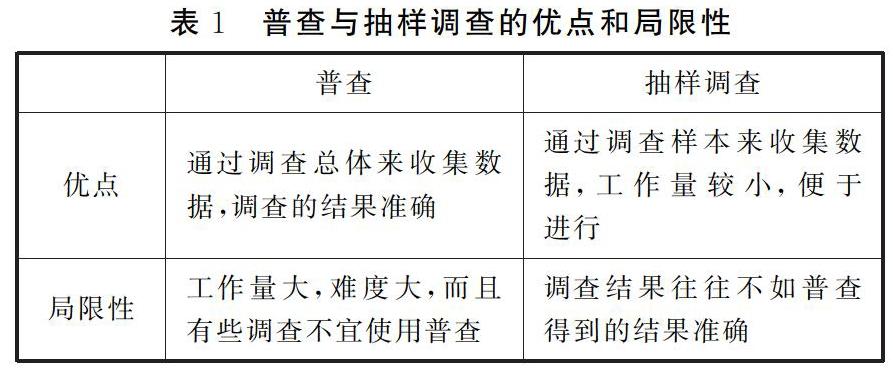
本堂課基于學生最近正在籌備的平板支撐大賽(plank)推進,首先提出問題1“你們組的同學平板支撐堅持的時間”,讓學生辨析其中的總體和個體。接著引出問題2“我們班同學每天運動時間”,讓學生辨析其中的總體和個體,以期達到對普查相關概念了解,并且能夠熟練應用的目的。然后分別向學生拋出問題3“全國所有初中生每天運動所用時間”,問題4“調查濟南市當天空氣PM2.5指數”,問題5“學校采購的200發發令槍子彈的質量”。以上三個問題還適合繼續用普查的方法進行調查嗎?為什么呢?通過學生討論,歸納出當“樣本量較大、客觀條件受限、調查具有破壞性”時不再適合繼續用普查,而應該轉向抽樣調查,繼續沿用上述例子讓學生概括其中的總體、個體、樣本和樣本容量。同時用表格概括出普查和抽樣調查的優點以及局限性(表1)。
通過表格呈現解決學生提出的“有沒有無論人數多少必須進行抽樣調查或必須進行普查的情況”這一問題。當所需數據精度較高時要進行普查,比如我國現在每10年進行一次的人口普查與農業調查。而當調查具有破壞性時則需進行抽樣調查,如必須調查一批導彈的射程半徑。
一般知識點呈現、特殊問題明晰之后通過習題測試了解學生對知識的掌握情況,判斷學生能否正確選擇普查或者抽樣調查。
針對抽樣調查中樣本如何選擇問題,通過舉反例的方式讓學生歸納總結出抽樣調查時樣本選擇必須具有代表性和廣泛性。一方面避免學生進行抽樣調查時選取的樣本誤差過大,另一方面也鍛煉了學生的歸納能力,把課堂還給學生。
用學生身邊的運動平板支撐貫穿本節課,在學習本節課內容的同時引發學生的思考,激發學生運動的潛意識,讓學生理解數學不只是理想化的生活模型,而是真正的“來源于生活,服務于生活”。
初識課淺,回首再望已是別有一番滋味。
參考文獻:
[1]茆詩松,程依明.概率論與數理統計教程[M].2版,北京:高等教育出版社,2011.
作者簡介:
宮明璐,山東省濟南市,山東大學附屬中學。

