分析思維特點合理設計教學

【摘要】本文以《求四邊形的內角和》教學為例，提出分析年段思維特點，精準確定教學重難點，為實現“學有所得”奠定基礎;教學中注重發散思維與聚合思維的彈性結合，通過直觀有效的教學手段，實現多途徑獲取知識的目的;教師根據思維活躍、注意力損耗等特點，把控教學，讓學生對課堂興趣盎然等教學策略。

【關鍵詞】精準定位 發散思維 聚合思維 教學設計

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2019）06A-0091-02

思維，是指在表象、概念的基礎上進行分析、綜合、判斷、推理等認知活動，思維的過程是感知、了解、接納的歷程，也是學習、運用與提高的關鍵方式。知識通過思考，才能逐步形成能力，并為個體生活與學習服務，讓學生受益終身。人類個體思維發展軌跡通常是從圖像、動作等直觀思維逐步過渡到語言、文字等深層次的抽象思維，而數學知識傳授的有效性是與受教育者的思維特點息息相關的。對數學學科的學習意義簡化表達——就是數理與相關能力的學習與培養運用。“如何讓學生理解抽象數理？”“如何讓學生運用數學規律解決生活中的問題？”這兩個議題的目的是“學以致用”，它一直是數學教師在教學中應著重解決的重要目標。這一目標驅動教師認真研究學生的思維特點，準確定位教學重難點，合理選擇教學手段，進而提高學習效果。因此，我們將思維與數學的契合點定位于“尊重思維發展特點，合理教授數學知識”上。基于此，筆者以四年級的一節數學課作為論點展開的載體，豐富論據，呈與讀者，望能達到交流提高的目的。

小學四年級是思維發展的關鍵時期，這個年段的小學生的思維由具體形象思維逐漸向抽象邏輯思維過渡，傳授的數理知識更趨向于概念化，教師要思考如何將概念與思維特點結合，實現教學效益最大化。教學時，筆者在科學理論依據支持下，分析教材、學生，從“教學重難點”“教學手段”“教學節奏”三方面科學定位與把控，將具體形象思維與數理教學有機結合，立體架構有效課堂，收效頗豐。筆者結合小學四年級數學上冊《求四邊形的內角和》的設計與教學，談談自己的思考。

一、分析第二學段思維特點，精準定位重難點，為實現“學有所得”奠定基礎

小學生思維發展通常以具體形象思維為主要起步形式，而后隨著年齡的增長，逐步過渡到抽象邏輯思維，但小學生呈現出的抽象邏輯思維很大程度上仍與直接的感性經驗密切相關，因此具體形象性教學非常重要。同時，根據《義務教育數學課程標準》（2011年版）的學段劃分，小學四至六年級屬于第二學段，這一學段的“知識技能”發展界定中有一明確的表述，即為“體驗從具體情境中抽象出數的過程”，由此，我們也可以清晰地認識到這個階段的學習仍舊在秉承直觀感受、理性總結的特點的基礎上，需要擴張學生的數理知識面，培養實際操作能力。教師在解析小學四年級學生思維發展銜接期的特點后，更應投入分析教材，合理確定教學重難點，讓學生能在直接的感官刺激中啟發思維，獲取難易適宜的知識。

《求四邊形的內角和》的教學重點就是讓學生掌握“四邊形的內角和是360°”這一數理。結合學生的思維特點與教材要求進行分析，其教學過程側重多途徑創設情境推導四邊形內角和的探究過程，即通過讓學生動手操作、多感官參與探究不同的推理實踐，直觀推理圖像與推理小結，充實學生對推理過程的積累，啟動思維概括性引子——“你在操作中發現了關于四邊形內角和的什么規律”來歸納數理，在準確定位教學重點后，筆者認真分析該學段學生的思維特點，將教學難點定位于通過設計有目的的聽、看、講、想、做等環節，激活學生感官參與學習，激發能動性，把抽象數理融入多元直觀操作中，讓學生自主掌握數理，懂得利用轉化思想推導四邊形的內角和，運用這項數學知識解決不同層次的相關問題，培養數學能力。

以上教學基調的設定，符合小學四年級學生的思維特點。“思維特點”與“教學內容”的科學綜合剖析凝練出準確的重難點，教學重難點精準定位將為教學手段的選擇提供精準靶向，教學策略更具方向性和有效性。科學設置目標，教師進行靶向發力，有目標地選擇多種教學策略傳授新知識，檢測效果，攀升關鍵知識的強化次數，將讓課堂教學事半功倍。

二、發散思維與聚合思維相結合，通過直觀有效的教學手段，實現多途徑獲取知識的目的

發散思維與聚合思維是數學思維中的兩種不同方式，其特點如下：發散思維的思維路徑呈光芒式散射，即在主導問題前置的情況下，圍繞問題展開多方面思考、多途徑研究、多向度答案預設……思維得到擴張;聚合思維如同“聚光”形態，在多種刺激與思考后進行的概括、歸納等表達，重點表現在數理總結環節。

發散思維與聚合思維的結合，是靶向發力策略之一，圍繞教學關鍵項，發散并聚合思維，讓學生對知識進行多角度思考后贊同觀點，在主動學習中收獲新知。這兩種思維也如同一只收放自如的大手，多種教學方法、探究手段形成“大手”本體，學生在專項探究活動中實踐操作，在活動中發現，從而在激發學生興趣的同時，訓練學生的思維，提高認知。在這個過程中還可呈現兩種思維訓練發展的延申模式：第一種就是從聚合思維數理出發，進行多向度、多角度深入整理，挖掘學生思維的廣度與深度，提高思維的敏捷性、靈活性、深刻性，進而形成優良的思維品質;第二種就是從發散思維的擴充入手，不斷充實發散脈絡，使各發散觀點具有可靠的依據，然后再逐步邁入聚合思維式的理性歸納，化繁為簡。

例如，在《求四邊形的內角和》“探索新知”環節，筆者先讓學生猜測：四邊形的內角和度數是多少？你能用什么方法來測量？這兩個問題就是本課教學知識的“關鍵項”。學生紛紛提出測量法、剪拼法、轉化法等一個個概念式方法，發散思維雛形初現。此時，由一個“測量方法選擇”引發出學生思維的發散，將有效激發學生的主觀能動性。教師迅速板呈這些方法，并給予學生充足的探究時間，鼓勵學生在規定時間內選擇多種方法測量，讓發散效果在實際操作中得以展現。接著，學生立刻拿出量角器、剪刀等工具，多途徑、多方法測量或計算四邊形的內角和。通過手眼腦的相互協作，學生的思維發展效果明顯，從最初的概念步入實際操作驗證，強化次數攀升，讓每個發散出來的觀點論證得以充實，學生感性認識更豐富。

基于以上效果，教師適時以歸納數理為目的訓練學生的聚合思維，必將取得較好的效果。教學時，筆者借助電子白板的實物投影、動畫、學科工具等功能，讓學生把各類探究方法一一演示，直觀演繹或計算;接著讓學生歸納出四邊形的內角和是360°。通過前期發散思維與聚合思維的升縮調控，學生已經掌握基本數理，緊接著筆者設計了判斷題、根據已知條件求四邊形某個角的度數、利用多種測量方法求多邊形內角和……順勢進行多層次的練習，學生不僅懂得靈活運用概念解決實際問題，而且還探究出了多邊形內角和的計算規律，大大提高了思考空間的深度與廣度。可見，發散思維與聚合思維的結合不僅讓學生在直觀形態中潛移默化地掌握知識，而且，通過聚合思維整理二次運用，培養了學生的數學實踐能力，進而有效踐行數學來源于生活的教學宗旨。

三、根據思維活躍、注意力損耗等特點，把控教學，讓學生對課堂興趣盎然，提高學習效果

經過長期的實踐與觀察，查閱兒童心理學相關書籍，筆者發現：四年級學生在課堂學習中，關于注意力損耗的研究通常以約8分鐘為一個時間段進行的，將40分鐘的課堂教學時間分為5段，注意力的損耗呈現逐段依次遞增的狀態。掌握這一規律后，筆者還發現：學生的思維活躍損耗規律也與注意力損耗有關系。為了降低學生的思維活躍損耗，激活思維，提高學習效果，筆者進行了相關對策的探究。目前發現，若在每個8分鐘學習段結束時換一種學習形式，比如：讀了8分鐘書后，換成寫練習、小組探究等另一種形式學習將能集中學生的注意力、保持思維活躍，保證學習質量。所以，把握好8分鐘時間節點設計有效、有趣、與上段教學有承接的學習內容與形式，調控好教學節奏等，學生對學習就會興趣盎然，效果較佳。

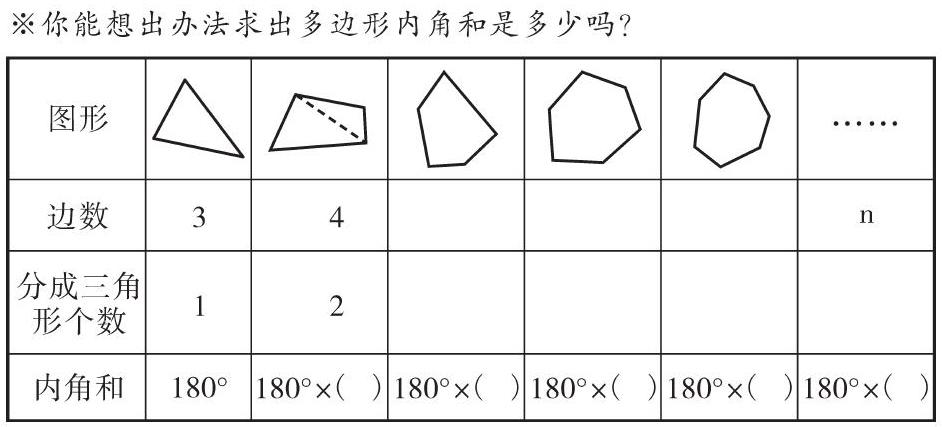
例如，在教學《求四邊形的內角和》一課時，筆者設計了“復習導入”“探索新知”“鞏固練習”“課堂總結”共四個環節，并在每個時間段內觀測、預測學生的學習狀態，采用動靜結合的形式，強化關鍵知識點。特別在最后一個8分鐘時段（即課堂第32-40分鐘），學生已熟練掌握并能應用四邊形內角和概念后，注意力與思維活躍已有所疲倦，此時筆者設計了一張學習卡（如下圖），讓學生通過四人合作學習探尋多邊形內角和，完成填空。這樣教學，將個人學習轉為四人合作，孩子們興致盎然，他們自主分工，有的負責探究操作，有的負責記錄、填空、計算……思維再次得以激活。通過類比5個多邊形的推理過程探尋多邊形內角和規律，四人組學生一致發現內角和運算規律是“180°×（n-2）”。這個環節的操作是利用了學習卡聚合學生資源、調整注意力，變小智慧為大數理，激活思維的能動性，同時也拓展了學生的認知。

總之，數學教學需要分析不同年齡段學生的思維特點，根據教學目標選擇合適策略是成功教學的基礎。在教學中把握時間節點，訓練思維，將讓學生獲得知識的同時形成能力、擴張認知。因此，教師要分析思維特點，合理設計教學，切實提高教學效率。

作者簡介：黎任（1977— ），男，漢族，廣西興業人，一級教師，玉林市優秀教師，玉林市先進教育工作者，玉林市教育系統“優秀共產黨員”，玉州區百佳教育工作者，課例《大家一起來》被評為教育部2016-2017年度“一師一優課、一課一名師”活動“優課”，主要研究方向：小學數學教育教學。

（責編 林 劍）