數形結合在初中函數教學中的應用

徐大香

【內容摘要】在數學學習實踐中，函數知識作為一個重要的知識體系，貫穿初中數學學習的始終。函數知識的學習需要學生借助對平面直角坐標系的有效理解和認識，通過將抽象性的函數知識與形象性坐標系有效地融合，讓學生在數形有效結合的基礎上，形成對函數知識的生動具體的認識體驗，從而達到對函數知識的有效認識理解過程。將抽象的函數知識與形象的直角坐標系有機地結合起來，讓學生在形象生動的認識圖形與數的關系的有效分析過程中，形成對函數知識的有效理解體驗過程。

【關鍵詞】初中數學 函數 數形結合 應用

著名數學家華羅庚指出：“數形結合百般好，數形分離萬事難”，數學課程標準也指出：“通過利用圖形來描述和分析問題，借助圖形直觀可以把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路”。因此，在初中數學教學實踐中，通過數形結合思想的有效滲透，讓學生在具體的數學學習實踐中，能夠有效地分析數形之間的具體關系，從而使學生形成對數量關系間的具體而生動的認識體驗，促進學生對問題的有效分析、推理、歸納和總結等，在有效的數形結合體驗中，實現對函數知識的生動認識體驗。因此，在初中數學教學實踐中，如何通過有效策略的實施，使學生在函數學習實踐中，通過數形結合，有效建構數學模型，形成對函數知識的生動形象的認識過程，在具體的教學實踐中可采取：

一、確立直角坐標系思想，構建代數與幾何聯系的橋梁

十七世紀法國著名數學家笛卡爾在一次偶然中發現，屋頂上的蜘蛛能夠沿著蜘蛛網左右上下爬行，他靈機一動，想到是否可以把蜘蛛看作一個點，它可以上、下、左、右運動，怎樣用一組數將蜘蛛的位置確定下來呢？由此衍生了直角坐標系理論。直角坐標系是代數與幾何之間的一座橋梁，將抽象復雜的數量關系知識以形象、生動的圖示形式展示出來，通過對直觀化的圖像分析，有效地降低了學生對抽象的數量關系分析的難度，提高了學生的學習效率。

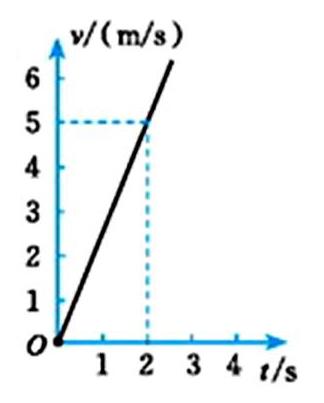
例如在學習《一次函數的應用》的實踐中，結合例題“某物體沿一個斜坡下滑，它的速度v（m/s）與其下滑時間t（s）的關系如圖所示。

（1）?? 寫出v與t之間的關系式;

（2）?? 下滑3s時物體的速度是多少？

教師在教學實施的過程中，教師將函數中的數量間的關系，以直觀的、形象的、直角坐標系的形式呈現在學生們的眼前，學生通過對圖像的觀察（因為圖像經過原點且呈一條直線，所以這是一個正比例函數的圖像）和題意分析可知v與t是正比例函數，由此可設其表達式為v=kt，在有效地結合已知量和變量之間的關系的基礎上，形成對一次函數的圖像以及數量關系間的有效認識體驗，通過有效分析，形成對問題的具體認識。因此，確定直角坐標系思想模型，讓學生在對函數問題的形象化的分析實踐中，達到問題的有效分析，合理判斷，并最終作出對函數問題的有效解答。

二、通過代數化幾何，化抽象為直觀

在初中數學函數學習實踐中，當數與數之間的關系，以文字式的形式展現在學生們的眼前時，以形象思維占優勢的初中生對函數的學習興趣難以有效地調動起來，而在具體的學習實踐中，通過將函數代數問題，轉換為幾何圖像，引導學生在圖像分析的過程中，形成對函數問題的有效認識體驗。

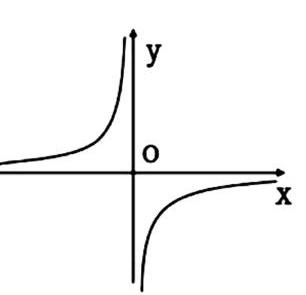
例如在學習《反比例函數的應用》的實踐中，分析例題若點（-2，y1）、（-1，y2），（2，y3）在反比例函數y=-2/x的圖像上，求y1，y2，y3之間的大小關系。首先根據函數的關系式可以畫出其相應的直角坐標函數圖像，根據圖像所在的象限可以判斷出三點所在的象限，進而利用函數圖像的增減性來判斷三個數的大小關系。以數化形，讓數量關系在直觀的圖像展示的過程中，更加簡便、并易于學生理解和認識，因而能夠極大地提高學生的學習效率。

三、確立數形互變思想，建構函數思維模型

學生在函數學習實踐中，能夠熟練地掌握函數的關系式與其圖像走勢之間的關系，并能夠根據具體的數量關系、列出正確的函數關系式，再結合函數關系式來進一步畫出函數圖像;反之也可通過函數圖像，分析出函數的增減性、判斷函數的各數量間的關系，進而列出相應的關系式，關系式是判斷函數關系的重要標志。確立了數形互變的思想，讓學生在具體的學習實踐中能夠正確、合理、有效地運用，從而使函數思維模型在學生的認知結構中得到有效地構建。

例如在學習《二次函數》的實踐中，根據二次函數的關系式，y=ax2+bx+c（a≠0），結合數據分析，能夠有效地形成對二次函數圖像的開口大小、方向以及對稱軸等內容的分析和概括，如二次項系數a決定著二次函數的開口方向和大小，當a>0時，二次函數拋物線圖像的開口向上;反之則拋物線圖像的開口向下;|a|越大，則二次函數的拋物線開口越小。二次項系數a和一次項系數b決定了對稱軸的位置，當兩者符號相同時，在對稱軸y軸的左側，反之則在右側。拋物線與x軸的交點個數則由Δ決定，當Δ=0拋物線與x軸只有一個交點;當Δ>0時，有兩個交點;Δ<0時，與x軸沒有交點。在對函數的相關數據的分析與理解的實踐中，實現數形的有機結合，從而達到對二次函數問題的有效理解和運用，實現課堂學習效果的有效提高。

總之，在函數教學實踐中，將數形結合思想在具體的教學實踐中的有效滲透，能夠極大地降低學習的難度，促進學生的理解、消化和吸收，因而更加有利于學習效果的突出顯現。因此，教師應將數形結合思想有效地滲透到數學教學的具體實踐中去，以使課堂效果得到良好的體現。

【參考文獻】

[1]初中數學教學中數形結合思想的運用分析——以反比例函數為例[J].劉志峰.課程教育研究（B）.2017（46）.

[2]初中數學教學中數形結合思想的應用[J].朱家宏.科技視界.2015（09）.

（作者單位：甘肅省永登縣武勝驛鎮初級中學）