淺談中考數學疑難問題訓練解決的方法
張藹東

反比例函數、一次函數、二次函數、三角形等的綜合題是中考的重點之一,出現在廣東中考解答題(三)的第23題,難度較大,但學生能否在該大題得到理想的分數,將影響學生在整份中考試卷的考試心理和得分,亦是拉開考生之間分數差距的題之一。在平時的復習備考中已復習函數等的相關知識,但計算準確性、答題速度和規范性需要加強。通過培養并形成將壓軸題化難為易的能力與意識,體會數形結合思想、轉化思想、函數思想、方程思想在數學問題解決中的作用,增強解決函數綜合題的自信心。在解決問題中能用待定系數法求函數表達式,能根據兩點之間線段最短,把求圖形最小周長轉化為求線段長問題,要掌握直角坐標系中求圖形面積的常用方法。
一、教師用PPT課件的幻燈片展示下列問題
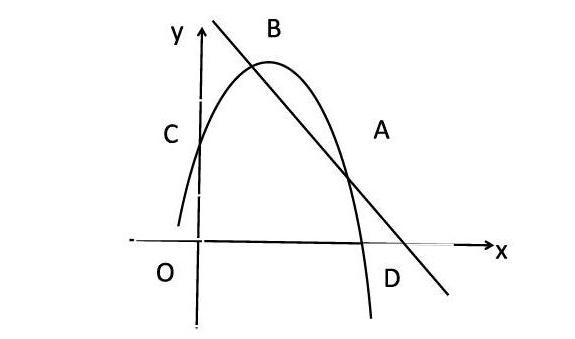
1.拋物線y=-x2+bx+c交y軸于點C(0,3),交x軸正半軸于D,并且與直線y=kx+b交于點A(2,3)和B(1,4),求一次函數表達式和拋物線y=-x2+bx+c的表達式。
2.兩點之間? ? ? ? 最短。
3.將軍飲馬問題。
4.二次函數取得最大值或最小值,與y=ax2+bx+c中的哪個量有關?
二、解決疑難問題的思路與方法
教師讓學生獨立思考,動筆做題,然后回答問題,從而總結出以下思路與方法:
1.因為點A、點B在直線上,所以把點A(2,3),B(1,4)代入y=kx+b得:k=-1,b=5故一次函數表達式為 y=-x+5,再把 A(2,3)、B(1,4)或C(0,3)代入y=-x2+bx+c得b= 2, c=3.所以,二次函數的表達式為:y=-x2+2x+3.
2.線段。
3.教師出示關于將軍飲馬的問題解決方法:(1)如下左圖,直線L的兩側兩點A、B,在直線L上求作一點P,使PA +PB 最小。
(2)如上右圖,直線L的同側兩點A、B,在直線L上求作一點P,使PA+PB 最小。
(3)如下左圖,點P 是∠MON 內的一點,分別在OM,ON 上作點A、B,使△PAB 的周長最小。
(4)如上右圖,點P,Q 為∠MON 內的兩點,分別在OM,ON 上作點A,B。使四邊形PABQ的周長最小。
4.與a值有關。通過上面的學習之后,教師自編一些相關聯的題目,檢查學生應用知識解題的情況,同時,也便于教師很好地了解學生已有的函數綜合的基礎、答題規范等。學生“動手做”是“感悟”的基礎。
5.教師出示自編題練習。如圖,拋物線y=-x2+bx+c交y軸于點C(0,3),交x軸正半軸于D,并且與直線y=kx+b交于點A(2,3)和B(1,4)。
(1) 在y軸上,是否存在一點E,使得ED+EB最小,若存在,求出這個最小值及點E的坐標;若不存在,請說明理由。
(2)連接BC,BD,CD,求△BCD的面積。
6.教師請學生思考并討論以下問題
①解決本題的第(1)問的關鍵是什么?如何才可以找到點E呢?
②你能說說第(2)問的解題思路嗎?你能用多少種方法?
教師先重點分析以下方法:(1)采用豎割法分割成兩個三角形進行計算
過點B作BF∥y軸,交CD于點M,過點C作CF∥x軸,交BD于點F。
(2)采用橫割法分割成兩個三角形進行計算。
讓學生5人一小組,分組討論,學生代表來說題,師生齊歸納:
①解決本題第1問的關鍵是:找點E。那如何找點E呢?只需要作點B或D關于直線(x軸或y軸)的對稱點,連接對稱點與另一點的交點即為所求點E,也就是將軍飲馬問題。
②第(2)問的解題思路及做法如下圖所示:
三、學生書寫解題過程
解:(1)存在。把B(1,4)和C(0,3)分別代入y=-x2+bx+c得
解得
所以拋物線的解析式為y=-x2+2x+3.令y=0,即-x2+2x+3= 0,解得x1=3,x2=-1故D(3,0).
作點B關于y軸的對稱B'(-1,4),連接DB'交y軸于點E,即點E為所求。設直線 D B'的解析式為:y=k1x+b,把 B'(-1,4)、D(3,0)分別代入上式解得:k1=-1,b=3,故直線DB'的解析式為:y=-x+3.當x=0時, y=3.所以點E的坐標為(0,3),點E與點C重合。所以ED+EB=ED+EB'=DB'=.
(2)(豎割法)過點B作BF∥于y軸,交直線CD于點M,則S△BCD=S△BCM+ S△BDM,因為OD=3,又因為C(0,3),所以設直線CD的解析式為:y=mx+n,把C(0,3)、D(3,0)分別代入上式解得:m=-1,n=3,故直線CD的解析式為:y=-x+3.把x=1代入上式得:y=-1+3=2,點M(1,2)故BM=4-2=2, 所以S△BCD=S△BCM+ S△BDM= BM(1+2)=×2×3=3.
通過一題多變,目的是培養學生的分析問題的能力、辯別圖形的能力、推理能力、計算能力、舉一反三的能力。
四、教師出示變式訓練一
如圖,拋物線y=-x2+bx+c交y軸于點C(0,3),交x軸正半軸于D,并且與與直線y=kx+b交于點A(2,3)和B(1,4)。
(1)求證:點B是拋物線y=-x2+bx+c的頂點坐標。
(2)在y軸上,是否存在一點E,使得以D、B、E三點所構成的三角形周長最小,若存在,求出這個最小值及點E的坐標;若不存在,請說明理由。
(3)在直線CD上方的拋物線上,是否存在一點B1,使得△B1CD的面積最大。
2.教師設計問題引導學生思考、分析:
①本題的第(1)問有什么特點?
②本題的第(2)問與第5題的第(1)問有什么不同?
③如果用豎割法解決本題,點M的坐標隨著哪個點的坐標變化而變化呢?
④點M的坐標和點B1的坐標應該怎樣設置呢?
五、變式訓練二:(改編)
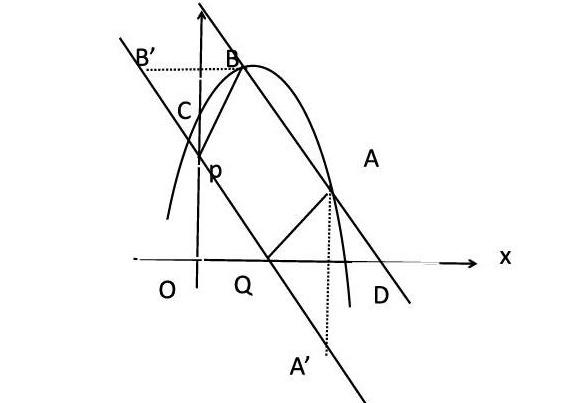
如圖,拋物線y=-x2+bx+c交y軸于點C(0,3),交x軸正半軸于D,并且與與直線y=kx+b交于點A(2,3)和B(1,4),若點 P是y軸的一動點,則在x軸上是否存在一點Q,使A、B、P、Q四點所圍成的四邊形周長最小。若存在,求出這個最小值及點P、Q的坐標;若不存在,請說明理由。
隨著題目的難度逐漸增加,目的是培養學生應用知識的能力以及知識遷移的能力。通過解決一道題以及其變式題來理解同一類問題的方法,以求達到做一道而通一類的效果。總結、反思和提煉函數綜合題的主要類型、解決問題的策略和主要數學思想方法。通過這樣的練習培養學生的總結能力,讓學生更好地掌握解決此類問題的方法與技巧,形成將壓軸題化難為易的能力與意識,提高學生的數學成績。

