基于深度學習理念的小學數學問題驅動教學

馬熙君

摘 要：問題驅動式教學作為提升小學數學課堂有效性、落實深度學習理念的重要載體，應該重點體現在引發學生的認知沖突，幫助學生形成深度學習的內心體驗上；應該體現在以問引思，對數學問題的解決進行合情預測中；應該拓展思維，體現在問題解決的開放性與創造上；應該落實于以問促用，幫助學生靈活解決現實問題的過程中。

關鍵詞：小學數學；問題驅動；深度學習

小學階段的數學知識具有一定的抽象性，而小學生的思維特點是以形象思維占優勢，抽象思維相對不足，小學生學習數學的困難主要就是由于這種斷層所致。通過教師提問為線索，引導學生自主探究知識并解決問題，可以打造有深度的數學課堂。下面以“圖形與幾何”的教學為例，說說對問題驅動式教學的體會。

一、以問引問，在認知沖突中引發深度學習體驗

一般而言，有效的數學課堂需要教師通過不斷制造認知上的“沖突”并在解決“沖突”的進程中把數學探究引向深入，因此教師需要充分利用學生的已知經驗，把它作為課堂提問的起點，這樣既能激發興趣，調動學生課堂參與的積極性，又能激活學生的課堂思維，使數學思維具有深刻性與厚度，提升學生的數學學習能力。

比如，在“長方形與正方形的面積”教學時，教師設計了這樣一個問題：講臺面的寬是80厘米，長是160厘米，而教室門的寬度是 120厘米，高是240厘米，請大家想一想，你認為講臺能順利通過教室門嗎？ 這個問題中，學生會思考不同的方案，會不斷地自我提問：講臺要能通過大門，有什么條件必須符合呢？題目中“門高”的“高”代表了什么意義？講臺進教室時應該是怎么樣調整好與門的位置關系？通過不斷嘗試學生會發現：一個長方形要通過另一個長方形，通常只要被通過的長方形面積比第一個長方形大，而且長與寬分別比第一個長方形長就可以了。這里還有通用文字表述與數學意義上的概念間的用詞不統一的問題，比如問題中說的門的高度其實應該是長方形的長。這里可見，這個問題為學生解決數學問題制造了一定的小陷阱，通過問題來制造學生頭腦中的疑惑，通過不斷提問與釋疑，使學生對問題的探究過程顯得妙趣橫生，充滿挑戰，有助于學生數學概念的建立，使學生形成學習的深刻體驗。

二、以問引思，在合理預測中開啟深度學習進程

學生深度學習的意義不在于得到了什么樣的知識結果，而是讓學生在學習進程中掌握了一種可持續性的學習方法與高階思維。比如對于圓周率的得出，最壞的做法莫過于告訴學生圓周率表示什么意思，他的值是多少。而較為科學的思路是教師要對課堂節點加以精準把握，聚焦核心問題，教師要具備核心問題的意識，對教學過程中可能會遇到的問題進行充分的考慮，設計出針對性較強的問題，以便使學生在思維受挫時能及時化解疑惑。惟其如此，學生的知識習得才具有深度，數學知識與數學技能的轉化也更為容易。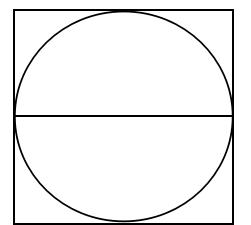

比如在教學“圓的周長”時，可以在實際測量確定周長與直徑的關系前，讓學生進行預測：1.如圖所示，你認為圓的周長大約是直徑的多少倍？（圖中正方形周長剛好是圓直徑的4倍）2.你認為圓的周長肯定比直徑的幾倍要大？（如果從半圓考慮，由于兩點之間線段最短，很明顯直徑小于半個圓周）。這樣，聯系已有知識與生活經驗，學生可以得出合理的預測：圓周長肯定比直徑的四倍小，也比直徑的2倍要大，所以圓周長大約是直徑的3倍左右。這樣學生通過合作、觀察與交流，就會對圓周長得到一個大概范圍的認知，提升了學生的課堂探究能力，為科學測量得出結果提供了合情預測，使知識習得成為一個從未知到已知，充滿戲劇性與挑戰性的過程。

三、以問拓思，培養深度學習的思維開放性

在小學數學教學中，運用問題驅動式教學，需要教師設計有一定思維廣度，體現思維開放性，能培養學生創造性思維的問題，從而使數學學習真正為促進數學思維訓練服務。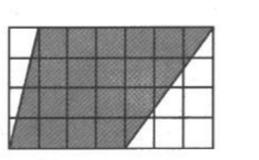

比如，在計算如右圖所示每一小正方形面積為1平方厘米的圖中的陰影部分面積時，大部分學生往往會從傳統的視角認為陰影部分是一個梯形，然后去尋找梯形的上、下底與高，再按部就班進行梯形面積的計算。假如教師提問：我們在計算圖中陰影部分面積時可不可以把他分割轉化為幾個熟悉的圖形來解決？如果我們從圖形外部分析，這塊陰影部分還可以怎樣計算？在教師的引導下，學生就可以有好幾種思路：①陰影部分面積等于中間長為4厘米寬為3厘米的長方形面積加上兩邊兩個小三角形面積。②陰影部分面積等于整個大長方形面積減去兩個不涂色的三角形面積。③先數出圖形中間整塊的小正方形塊數，再把周邊不是整塊小正方塊的面積進行拆、拼。這樣學生的問題解決思路就不再機械與單一，開放性的提問為學生的深度學習提供了開放性的思路，使數學學習的“山窮水盡”最終化為“條條道路通羅馬”的釋然與自信。

四、以問促用，促進深度學習的遷移應用

數學教學的根本目的在于培養學生靈活運用數學知識解決實際問題的能力。比如在長方形與正方形面積計算時，有這樣兩道題：①一輛可載重20噸的貨車，要運送一批長為5米，寬為1.2米的鋼板，每平方米鋼板的重量是30千克，這輛卡軍可以運送多少塊這樣的鋼板？②陳叔叔想在郊區一排長房子后建一個小型養雞場，雞場的一面可以靠墻，他買了36米長的鐵柵欄，請嘗試設計一個長方形或者正方形的養雞場，請問怎樣設計能讓養雞場的面積最大。

通過這兩個問題的設計，使學生把日常學習的面積計算知識運用到實際應用中去，特別是后一題，學生要將長方形周長與面積知識結合起來，而且沒有明確要求是設計長方形還是正方形，學生需要不斷嘗試，才能找到科學合理的方案。所以聯系學生的生活實際，讓數學學習與實際問題的解決緊密聯系起來，有助于促進深度學習的遷移運用，使知識的運用、技能的形成更為牢固、更有實際價值。

總而方之，問題驅動式教學是提升小學數學課堂有效性、落實深度學習理念的重要載體。深度學習不代表一定是有難度的學習，而是幫助學生開展積極的數學思維活動，尋求有效的思維策略的創造性的學習，是落實小學生數學學習核心素養的重要一環。

參考文獻

[1]宋慧嫻，劉榮.小學數學基于問題解決的深度學習模式探索[J].小學數學教育，2016（5）。

[2]屈桂芬.引領學生深度學習路徑與策略[J].江蘇教育研究，2017（10）。