基于智慧課堂的高中數學新授課教學模式的構建策略

陳全勇

[摘? 要] 新技術的應用使得傳統課堂教學迎來革新，而智慧課堂的實施能夠有效彌補傳統課堂存在的局限，可以使得課堂更加便捷高效，學生的合作意識逐漸增強，教學評價也更加精準. 文章以“空間向量的正交分解及其坐標表示”教學為例深入探究了智慧課堂教學模式的構建策略.

[關鍵詞] 智慧課堂;高中數學;新授課;教學模式

作為當前教育信息化發展的新動向，智慧課堂以動態學習分析和評價為核心將新一代信息技術應用到教學全過程之中，以實現構建高效課堂的目的，其本質是在智慧教育背景下如何開展教學. 因此，以新授課教學為例，就高中數學教學中如何實施智慧課堂談談筆者自身的實踐與思考.

■高中數學智慧課堂新授課教學模式構建

結合多元智能理論、建構主義學習理論，筆者設計出了如下高中數學智慧課堂新授課教學模式，如圖1所示.

1. 課前階段

（1）教案設計. 教師應充分分析智慧課堂信息化平臺推送的學生作業成績，并依據學生實際，設計出本節課程的教學目標、內容以及方法等.

（2）預習測評. 教師應將課件、微課、教輔資料和課前預習任務等通過網絡教學平臺推送至每個學生，要求學生在線完成并提交. 值得說明的是，在此過程中，若學生遇到相關疑惑或問題時，應通過網絡交流平臺及時與教師和其他同學進行探討交流.

（3）教案重構. 為了使得教學更加精準，教師應根據預習檢測統計反饋情況，及時調整和優化教學方案，最大限度地達到以學定教的目的.

2. 課中階段

（1）課題導入. 教師應鼓勵學生就課前預習情況進行反饋，提煉出學生的共性問題，并圍繞這些共性問題創設情境，明確學習探究任務.

（2）探究學習. 學生以小組為單位，圍繞學習任務和課程要求開展探究性學習，并及時在組際間開展交流活動，教師適時引導學生進行評價和總結■[1].

（3）變式訓練. 為了有效檢測學生的學習成果，促使學生不斷查漏補缺，教師應將具有代表性的客觀題目和相關的變式推送至每個學生進行實時診斷和檢測. 值得注意的是，為了有效確保每一個學生都能參與到教學中來，教師應嚴格監控學生的答題時間和注意力.

（4）總結提升. 為了進一步幫助學生對所學知識進行鞏固和提升，結合檢測反饋結果，可引導學生進行全面分析、評價[2]■，不斷總結和點評教學中的重難點知識.

3. 課后階段

（1）課后作業. 教師應根據教學內容和學生學習的情況，針對性地設置課后鞏固習題，并及時通過網絡教學平臺進行推送.

（2）微課輔導. 針對課后作業批改情況以及學生的問題疑惑，教師應有針對性地推送相關微課，有效幫助學生拓展提升和查漏補缺.

（3）反思評價. 為了有效進行交流，教師還應鼓勵學生通過網絡交流平臺進行探討交流，分享自己的學習心得、自己制作的微視頻和問題疑惑，并及時組織學生進行個人自評和互評，為后續授課做好準備.

■高中數學智慧課堂新授課教學模式之教學實踐

僅有相關理論是不夠的，為了深入探究智慧課堂教學模式，達到理論與實踐相結合的目的，筆者以“空間向量的正交分解及其坐標表示”教學為例進行實踐探索.

1. 課前階段

為了掌握學生對課前所學知識的學習情況，筆者將以下復習、預習內容和課前作業通過網絡交流平臺推送至學生，要求學生獨自完成，并及時在線提交，以自己的疑惑與其他學生進行探討交流.

（1）若向量a與非零向量b共線，那么有且僅有一個實數λ，使得a=______.

（2）在同一平面內，若e1和e2是兩個不共線的向量，那么，若對于該平面內任意一個向量a，有且僅有一對實數λ1，λ2，使得a=______. 即平面內任意一個向量都可以用______個______的向量進行表示■[3].

（3）對于空間中任意一個向量p，存在一個有序實數組（x，y，z），使得p=______. 此時x，y，z被稱作向量p在單位正交基底e1，e2，e3下的坐標，記為______.

（4）如圖2，已知空間四邊形OABC，■=a，■=b，■=c，MA=MO，NB=NC，則向量■表示為（? ）

A. ■a+■b+■c？搖

B. ■a-■b+■c？搖

C. -■a+■b+■c

D. ■a+■b-■c

隨后，就學生課前預習的反饋情況進行統計，了解學生預習和做題過程中存在的問題，并及時優化和調整教案.

2. 課中階段

為了檢驗課前學習效果，筆者及時組織學生溫故共線向量定理和平面向量基本定理，要求學生類比平面向量去猜測空間向量如何表示，并要求學生以小組為單位，探究以下問題：

（1）已知p是空間中的任意一個向量，a，b，c是空間中三個不共線的向量，并且■=a，■=b，■=c，試用a，b，c表示向量p.

（2）探究空間向量的正交分解及其坐標表示.

隨后，要求學生將探究成果通過照片的形式予以上傳，并引導學生思考p=■=xa+yb+zc中x，y，z是否唯一.

最后，要求學生自我歸納總結出空間向量基本定理，引導學生進一步深刻理解“任意”“不共線”“向量組”“單位向量”“唯一實數組”等詞語的具體含義;并呈現出以下練習題目，要求學生在規定的時間內獨自完成.

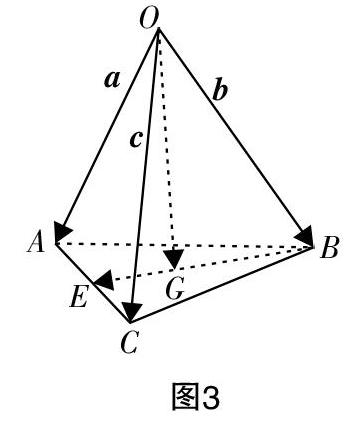
（1）如圖3所示，已知空間四邊形OABC，■=a，■=b，■=c，G為△ABC的重心，EA=EC，若以{a，b，c}為空間基底向量，則試求向量■和向量■.

（2）如圖4所示，已知長方體ABCD-A′B′C′D′，若AB=3，AD=4，AA′=2，EC=ED，FC′=FD′，試求向量AF和AE的坐標.

3. 課后階段

結合課堂變式練習實時檢測情況，筆者及時布置了課后作業，并針對學生的反饋意見、作業批改情況以及學生的學情，錄制了講解微課視頻，進一步幫助學生拓展提升和查漏補缺，并要求學生就本次所學知識及時進行討論交流，鼓勵學有余力的學生就某一具體練習題目制作微視頻上傳共享.

總之，作為信息技術與教育融合的新產物，智慧課堂確實有眾多優勢，但從理論到實踐還需要不斷地探索總結[4]■. 然而，以信息化方向邁進推送教育教學模式的變革和創新的趨勢是不會改變的，我們相信，隨著智慧課堂教學模式的不斷成熟和實踐，定能提高高中數學教學的質量和水平.

參考文獻：

[1]? 羅蕊. 智慧課堂教學模式在高中數學教學中的應用研究[D]. 云南師范大學，2019（05）.

[2]? 郭有春. 基于核心素養的高中數學智慧課堂的創建[J]. 數學教學通訊，2019（21）.

[3]? 王佩，趙思林. 空間向量的正交分解及坐標表示的教學設計[J]. 中學教研（數學），2018（01）.

[4]? 龐靜. 構建高中數學智慧課堂的思考[J]. 數學教學通訊，2018（24）.