制造“麻煩”，提升學(xué)生數(shù)學(xué)思維

陳曉琳

[摘要]發(fā)展學(xué)生的數(shù)學(xué)思維能力是數(shù)學(xué)教學(xué)的核心。在數(shù)學(xué)學(xué)習(xí)中，學(xué)生習(xí)慣于待在思維舒適區(qū)而形成思維定式，對(duì)此，教師可以故意制造“麻煩”，打破學(xué)生的思維定式，從而幫助學(xué)生開(kāi)拓思路，不斷提升數(shù)學(xué)思維能力。

[關(guān)鍵詞小學(xué)數(shù)學(xué);制造“麻煩”;思維定式;發(fā)散思維

[中圖分類(lèi)號(hào)]G623.5

[文獻(xiàn)標(biāo)識(shí)碼]A

[文章編號(hào)]1007-9068（2020）32-0044-02

數(shù)學(xué)思維是數(shù)學(xué)教學(xué)活動(dòng)的靈魂，發(fā)展思維能力是數(shù)學(xué)教學(xué)的核心。因此，在小學(xué)數(shù)學(xué)教學(xué)中，要想提高教學(xué)質(zhì)量，提升學(xué)生的數(shù)學(xué)核心素養(yǎng)，就要運(yùn)用各種有效手段激起學(xué)生思維的火花。在課堂中故意制造“麻煩”，讓學(xué)生在解決“麻煩”中打破思維定式、彌補(bǔ)思維漏洞、開(kāi)拓解題思路，最終學(xué)會(huì)有效思考，是提升學(xué)生數(shù)學(xué)思維的有效途徑。

一、在思維疏漏處制造“麻煩”，彌補(bǔ)思維漏洞，提高思維嚴(yán)謹(jǐn)性

要在課堂上適當(dāng)?shù)刂圃臁奥闊保梢詮膶W(xué)生思維疏漏處著手。正如雨果所說(shuō)：“在泥土下面，黑暗的地方，才能發(fā)現(xiàn)金剛鉆;在深入縝密的思維中，才能發(fā)現(xiàn)真理。”在學(xué)生的思維疏漏處制造“麻煩”，能加深學(xué)生對(duì)重點(diǎn)、難點(diǎn)知識(shí)的理解，彌補(bǔ)其思維方式上的漏洞，從而提高學(xué)生的思維嚴(yán)謹(jǐn)性，提升思維品質(zhì)。

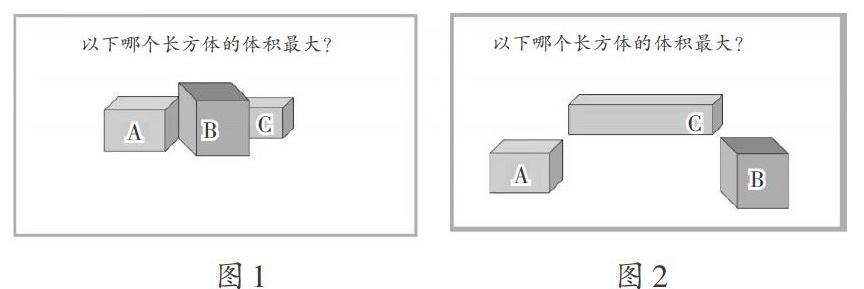
例如，在滬教版教材五年級(jí)第二學(xué)期“長(zhǎng)方體的體積”一課中，我在引入部分有意地制造了“麻煩”。我先給出三個(gè)不同大小的長(zhǎng)方體（如圖1），其中一個(gè)長(zhǎng)方體部分被遮擋，然后提問(wèn)：“這三個(gè)長(zhǎng)方體中，哪個(gè)長(zhǎng)方體的體積最大？”部分學(xué)生毫不猶豫地指出B長(zhǎng)方體的體積最大，因?yàn)樗瓷先プ畲蟆Ｓ胁糠謱W(xué)生表示反對(duì)，覺(jué)得無(wú)法比較，因?yàn)镃長(zhǎng)方體被擋住了。接著又有學(xué)生補(bǔ)充道：“C長(zhǎng)方體的寬和高沒(méi)有被擋住，長(zhǎng)被擋住了，因?yàn)殚L(zhǎng)不知道，所以不能確定哪個(gè)長(zhǎng)方體的體積最大。”最后，學(xué)生把問(wèn)題歸結(jié)為：只要知道C長(zhǎng)方體的長(zhǎng)，就能知道哪個(gè)長(zhǎng)方體的體積最大。在此基礎(chǔ)上，我移動(dòng)A長(zhǎng)方體和B長(zhǎng)方體，使C長(zhǎng)方體完全露出來(lái)（如圖2），繼續(xù)提問(wèn)：“現(xiàn)在C長(zhǎng)方體沒(méi)有被遮擋了，哪個(gè)長(zhǎng)方體的體積最大？”學(xué)生發(fā)現(xiàn)還是不能確定，只有給出了具體的數(shù)據(jù)，通過(guò)計(jì)算才能判斷。于是，我順理成章地引導(dǎo)學(xué)生探究長(zhǎng)方體體積與長(zhǎng)、寬、高的關(guān)系，進(jìn)而探究長(zhǎng)方體體積計(jì)算公式的推導(dǎo)。

我在引人中給學(xué)生制造“麻煩”，目的是讓學(xué)生發(fā)現(xiàn)長(zhǎng)方體的體積與其長(zhǎng)、寬、高都有關(guān)，從而引導(dǎo)學(xué)生去推導(dǎo)長(zhǎng)方體體積的計(jì)算公式。在解決“麻煩”中，學(xué)生不斷發(fā)現(xiàn)思考過(guò)程中的漏洞，并在一次比一次更深入的分析中，逐漸將問(wèn)題看得更全面、更透徹、更本質(zhì)。如此，學(xué)生思維的嚴(yán)謹(jǐn)性就提高了。

二、在思維矛盾處制造“麻煩”，厘清思考過(guò)程，發(fā)展思維邏輯性

數(shù)學(xué)學(xué)習(xí)中經(jīng)常會(huì)出現(xiàn)容易產(chǎn)生思維矛盾的問(wèn)題，這些矛盾通常也是教學(xué)的重點(diǎn)與難點(diǎn)。這些矛盾的問(wèn)題往往包含兩種不同的結(jié)論，它們的推導(dǎo)似乎都邏輯嚴(yán)密，但又互不相容。學(xué)生在沒(méi)真正明晰概念前，會(huì)處在混淆不清、似是而非的矛盾中。其實(shí)，適度的思維矛盾不僅能激發(fā)學(xué)生的求知探索欲望，而且能讓學(xué)生在解決思維矛盾中真正把握住知識(shí)的重難點(diǎn)。因此，教師可以在思維矛盾處制造“麻煩”，引導(dǎo)學(xué)生厘清思路，發(fā)展思維的邏輯性。

例如，在滬教版教材五年級(jí)第二學(xué)期“正數(shù)與負(fù)數(shù)”一課中，我先請(qǐng)6位學(xué)生各舉一個(gè)負(fù)數(shù)的例子填入負(fù)數(shù)圈中（如圖3），讓學(xué)生判斷是否都是負(fù)數(shù)，并說(shuō)出判斷的依據(jù)。學(xué)生A回答：“因?yàn)樗鼈兌加胸?fù)號(hào)。”我繼續(xù)追問(wèn)：“都有負(fù)號(hào)是表層的理解，更深層次的依據(jù)是什么？”學(xué)生開(kāi)始小聲討論，隨后學(xué)生B回答：“因?yàn)樗鼈兌急?小。”所有學(xué)生都表示同意。于是，負(fù)數(shù)的概念就被總結(jié)為：負(fù)數(shù)是比0小的數(shù)。接著，我引出正數(shù)，同樣讓5位學(xué)生各舉一個(gè)正數(shù)的例子填入正數(shù)圈中（如圖4）。要注意的是，我還在正數(shù)圈中填入了數(shù)字0。我繼續(xù)提問(wèn)：“這樣填大家有異議嗎？”學(xué)生C指出：“正數(shù)包括0嗎？”這個(gè)爭(zhēng)議，是思維矛盾點(diǎn)，也是本節(jié)課的重難點(diǎn)，更是理解正數(shù)與負(fù)數(shù)概念的關(guān)鍵。我讓學(xué)生就爭(zhēng)議發(fā)表自己的看法。學(xué)生D認(rèn)為，因?yàn)樨?fù)數(shù)是比0小的數(shù)，所以0就是正數(shù)。學(xué)生E認(rèn)為，0前面沒(méi)有負(fù)號(hào)，所以是正數(shù)。學(xué)生F認(rèn)為，0表示什么也沒(méi)有，而正數(shù)表示有一定的數(shù)量，所以0不是正數(shù)。學(xué)生G認(rèn)為，正數(shù)是比0大的數(shù)，所以0不是正數(shù);0既不是正數(shù)也不是負(fù)數(shù)。通過(guò)學(xué)生的闡述，正數(shù)和負(fù)數(shù)的概念逐漸清晰，這個(gè)矛盾點(diǎn)“0”就成了區(qū)分正負(fù)數(shù)的關(guān)鍵數(shù)。通過(guò)討論，最終大家都同意學(xué)生G的觀點(diǎn)。最后，我總結(jié)道：“正數(shù)是比0大的數(shù)，負(fù)數(shù)是比0小的數(shù)，所以0既不是正數(shù)也不是負(fù)數(shù)。”

在負(fù)數(shù)的學(xué)習(xí)中，我故意制造了“麻煩”——0，將它設(shè)置成思維矛盾點(diǎn)，讓學(xué)生通過(guò)發(fā)表各自的看法，從而真正認(rèn)識(shí)0，深刻地理解負(fù)數(shù)與正數(shù)的概念。學(xué)生在闡述的過(guò)程中，不僅逐漸厘清了思路，也逐漸發(fā)展了思維的邏輯性。

三、在思維定式處制造“麻煩”，打破思維定式，提升思維靈活性

在數(shù)學(xué)教學(xué)中，教師常常有這樣的困惑：學(xué)生只會(huì)機(jī)械地處理曾經(jīng)遇到過(guò)的數(shù)學(xué)問(wèn)題，問(wèn)題一旦變化就不能靈活應(yīng)對(duì)。究其原因，是學(xué)生的思維缺乏靈活性。思維的靈活性指學(xué)生的思考不受思維定式的限制，能從多角度去分析和解決問(wèn)題。思維靈活的學(xué)生能抓住事物間的內(nèi)在聯(lián)系和本質(zhì)特征，能透過(guò)現(xiàn)象看問(wèn)題，善于聯(lián)想，能把知識(shí)融會(huì)貫通，從而解決問(wèn)題。因此，教師在課堂中可以通過(guò)制造“麻煩”，打破學(xué)生的思維定式，幫助學(xué)生從多角度去解決問(wèn)題，從而提升思維靈活性。

例如，在滬教版教材一年級(jí)第二學(xué)期“度量”一課中，在學(xué)生掌握了用直尺測(cè)量物體的長(zhǎng)度的方法后，我拿出一把斷尺（0刻度損壞，刻度起點(diǎn)為2cm3mm），提問(wèn)：“老師的直尺斷了，還能測(cè)量嗎？”有部分學(xué)生表示，要從0刻度開(kāi)始量，0刻度沒(méi)有了，那么就不能測(cè)量。于是，我讓學(xué)生進(jìn)行討論，找出測(cè)量的方法，越多越好。經(jīng)過(guò)討論，許多學(xué)生找到了方法。學(xué)生A說(shuō)：“可以把2cm3mm作為起點(diǎn)去量。”學(xué)生B說(shuō)：“把2cm3mm作為起點(diǎn)有點(diǎn)麻煩，可以選擇3cm作為起點(diǎn)。”學(xué)生C說(shuō)：“把10cm作為起點(diǎn)更方便。”學(xué)生D說(shuō)：“可以把直尺反過(guò)來(lái)看，把最后面的刻度20cm作為起點(diǎn)。”針對(duì)教師制造的“麻煩”，學(xué)生通過(guò)交流討論，思路打開(kāi)了，打破了以0刻度作為起點(diǎn)測(cè)量的思維定式。

學(xué)生形成思維定式的一個(gè)原因是一直處在思維舒適區(qū)，所以教師在課堂中要適當(dāng)?shù)亟o學(xué)生制造“麻煩”，打破學(xué)生的思維舒適區(qū)，讓學(xué)生不得不從其他角度去看待問(wèn)題、尋找方法，從而打破思維定式，提升思維的靈活性。

四、在思維延伸處制造“麻煩”，開(kāi)拓解題思路，激活思維發(fā)散性

在教學(xué)過(guò)程中，如果只關(guān)注培養(yǎng)學(xué)生掌握一種解題思路的定性思維，無(wú)疑會(huì)限制學(xué)生的創(chuàng)造性。在課堂教學(xué)中促進(jìn)學(xué)生進(jìn)行發(fā)散性思考，不僅能使學(xué)生掌握知識(shí)的內(nèi)在聯(lián)系，而且能幫助學(xué)生開(kāi)拓思路，發(fā)散思維。教師有意識(shí)地在思維延伸處制造“麻煩”，是激活學(xué)生發(fā)散性思維的一個(gè)有效途徑。

例如，在滬教版教材一年級(jí)第二學(xué)期“百以內(nèi)數(shù)的表示”一課中，教師通常是借助百數(shù)圖來(lái)讓學(xué)生掌握百以內(nèi)數(shù)的表示，雖然學(xué)生能掌握課程內(nèi)容，但學(xué)習(xí)的過(guò)程是比較被動(dòng)的，在思維上也是比較定性。我在課堂中則通過(guò)讓學(xué)生小組合作，用花生擺出41來(lái)引入課題。學(xué)生擺好后，我故意制造“麻煩”：“能否只用5顆花生來(lái)表示41？”部分學(xué)生聽(tīng)到這個(gè)問(wèn)題感到很詫異，隨后我讓學(xué)生進(jìn)行小組討論。討論過(guò)后，許多小組有了不同的解決方法（如圖5）。小組A用4顆大的花生表示40，1顆小的表示1，合起來(lái)就是41。小組B把4顆花生橫著放表示40，1顆花生豎著放表示1，合起來(lái)就是41。小組C把4顆花生一起放在十位上，表示40，1顆花生單獨(dú)放在個(gè)位上，表示1，合起來(lái)就是41。這時(shí)，我拿出計(jì)數(shù)器，請(qǐng)小組C將我準(zhǔn)備好的5顆花生串入計(jì)數(shù)器上。在小組C的協(xié)助下，我引出了數(shù)位的概念，學(xué)生也在活動(dòng)經(jīng)歷中掌握了知識(shí)的內(nèi)在聯(lián)系。

這樣制造“麻煩”，讓學(xué)生在解決“麻煩”的過(guò)程中打破了只用一種解題思路去解決問(wèn)題的單一思維。在小組討論和動(dòng)手實(shí)踐的過(guò)程中，學(xué)生的思路逐漸打開(kāi)，呈現(xiàn)出了思維的活力，激活了發(fā)散性思維。

在學(xué)習(xí)過(guò)程中，學(xué)生如果一直待在思維舒適區(qū)就會(huì)喪失思考的需求與能力，久而久之，思維就會(huì)固化。因此，教師在課堂上要有意地制造一些“麻煩”，讓學(xué)生產(chǎn)生思考的需求。學(xué)生在解決“麻煩”的過(guò)程中就能不斷發(fā)展思維，提升思維品質(zhì)。

（責(zé)編 吳美玲）