“數學抽象”素養在高中數學課堂教學中的培養


“數學抽象”素養在高中數學課堂教學中的培養
——以函數的單調性概念的課堂教學策略為例
陳展潘
(惠陽中山中學 廣東 惠州 516000)
【摘要】? 高中數學新的課程標準(2017版)提出了高中學生在數學學習中應培養好數學抽象、邏輯推理、數學運算、直觀想象、數據分析、數學建模六大核心素養。其中數學抽象在六大核心素養中是最重要的,同時是培養學生數學思維能力最重要的一環。因此在平時的數學課堂教學活動中,注重數學抽象能力的培養,有利于學生養成一般性思考問題的習慣,有利于學生更好地理解數學概念,有利于學生對知識的理解和掌握,有利于提高學生的數學成績。
【關鍵詞】? 核心素養 培養 單調性 課堂教學 數學抽象
【中圖分類號】? G633.6 ? ? ? ? ? ? ? ? ?? ? 【文獻標識碼】? A 【文章編號】? 1992-7711(2020)04-155-02
一、數學抽象的內涵及其相關概念
通俗地講數學抽象是通過觀察、分析,撇開數學對象的外部的、偶然的、非數學的(物理的、化學的、社會的)東西,分析與提煉出其本質、內在、必然的東西,從空間形式和數量關系上揭示數學對象的本質和規律的一種數學研究方法。數學抽象素養是通過對具體而生動的數學問題進行分析與提煉,概括出一般結論,并應用于解決新的問題之中來體現。數學抽象反映了數學的本質特征,是數學六大核心素養的核心,貫穿于數學教學的全過程。從內容上看,數學抽象包括數學概念、命題、方法和體系的抽象。
二、數學抽象的培養在高中數學課堂教學的現狀
在高考成績的壓力下,很多教師為了追求學生成績,放棄了很多概念的教學,過分的強調解題技巧、方法和解題的步驟,再進行強化式的訓練也就是題海戰術,這就造成學生會解題、能得分但不知道知識的產生、發展過程。學生對概念課的學習不感興趣,認為考試不考,課堂枯燥,只要能做題就行了,這就造成學生數學抽象能力難于形成。
三、以函數的單調性概念的課堂教學策略為例談培養學生的數學抽象能力
(一)教材地位與作用
《函數的單調性》是人教版必修一第1.3節的內容,本節教學內容含單調性的概念、單調性的判斷及證明。是學生在初中學習了自變量與函數值變化關系的基礎上對函數的更深層次理解,也是函數概念和函數圖像學習的延續,函數的單調性是函數的重要性質,是研究函數的重要手段和工具,對以后函數的最值、基本初等函數、導數等知識的教學具有重要的作用。由于它還是初等數學和高等數學銜接的樞紐,所以在本學科具有不可替代的地位和作用,是本學科的核心內容。
(二)教學過程分析
1.創設情景,引入新課
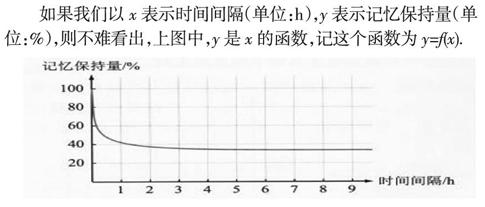
活動一:我們知道,“記憶”在我們的學習過程中扮演著非常重要的角色,因此有關記憶的規律一直都是人們研究的課題.德國心理學家艾賓浩斯曾經對記憶保持量進行了系統的實驗研究,并給出了類似下圖所示的記憶規律。
如果我們以x表示時間間隔(單位:h),y表示記憶保持量(單位:%),則不難看出,上圖中,y是x的函數,記這個函數為y=f(x).
問題1:這個函數反映出記憶具有什么規律?你能從中得到什么啟發?
設計意圖從學生熟悉的生活實際出發,激發學習興趣和求知欲望。
活動二:閱讀教材,并回答“思考”問題畫出下列函數的圖象,觀察其變化規律:
1. f(x)=x
①從左至右圖象上升還是下降__________________? ?
②在區間? ? ? ? ? ?上,隨著x的增大,f(x)的值隨著__________________.
③若x1 2. f(x)=-2x+1 從左至右圖象上升還是下降______________________________ ? 在區間? ? ? ? ? ? ? ? 上,隨著x的增大,f(x)的值隨著_________________ . ③若x1 3. f(x)=x2 ①在區間_________________上,f(x)的值隨著x的增大而減少,此時若x1 ②在區間_________________上,f(x)的值隨著x的增大而增大。此時若x1 設計意圖:從學生現有知識出發來研究新問題,尊重學生的認知的規律。從最簡單的一次函數和二次函數出發,避免了學生對新知識的恐懼和怕難的心理,有利于學生歸納總結出增、減函數的概念,培養學生的數學抽象能力。 2.抽象新知,經歷過程 活動三:通過前面的分析得到單調函數的概念:函數單調性定義 知識點1.增函數 一般地,設函數f=f(x)的定義域為,如果對于定義域內的某個區間D內的任意兩個自變量x1,x2,當x1 知識點2. 減函數 一般地,設函數y=f(x)的定義域為,如果對于定義域內的某個區間D內的任意兩個自變量x1,x2,當x1 設計意圖:從特殊到一般,學生數學抽象得到提升,形成基本概念。 知識點3.函數的單調性定義 如果函數y=f(x)在某個區間上是增函數或是減函數,那么就說函數y=f(x)在這一區間具有(嚴格的)單調性,區間D叫做y=f(x)的單調區間。 設計意圖培養學生的類比能力,體現數學的聯系與變通,再次強化數學抽象能力。 幾點說明: (1)函數的單調性是在定義域內的某個區間上的性質,是函數的局部性質; (2)從數的角度敘述增減函數:必須是對于區間D內的任意兩個自變量x1,x2 ①x1 ②函f(x)為增(減)函數,f(x1)>f(x2)(<),則x1>x2(<) ③函數f(x)為增(減)函數,x1 (3)從形的角度敘述增減性: 設計意圖:從文字、式子、圖形三個方面結合,幫助學生理解函數單調的概念,培養了學生的直觀想象、數學抽象和邏輯推理的能力,更有利于學生對函數單調性概念的理解。 活動四:例題教學 例1畫出下列函數的圖象,結合圖象說出函數的單調性。 1. y=x2+2x-1 ? ? 2. y= 例2證明函數f(x)=x+在是單調減函數。 設計意圖:由一般到特殊,把抽象數學應用到具體的習題中,更好地理解概念,同時培養了學生的邏輯推理能力,學會用數學思維思考問題,不等式應用也得到了具體體現。 活動五:鞏固訓練 證明函數y=x+在(-1,0)上為減函數。 設計意圖:再次強化訓練,體現邏輯推理和數學運算能力。 (三)教學反思 函數的單調性的概念是高中數學概論教學中的一個難點,也是高中學生學習函數的第一個性質,由于抽象能力較差,所以學生對概念的形成存在一定的困難,本節課從生活實際例子出發,再從學生最熟悉的一次函數和二次函數等特殊情況來研究函數單調性,最后探究、抽象出函數單調性的概念。讓學生感受到數學來源以生活,避免了學生課堂傻傻的聽,課下泛泛的補的不良習慣。體現了數學教學應讓學生經歷完整的抽象過程、參與完整的抽象活動。真正體現了數學課堂教學應再現抽象的過程,強化抽象的過程。通過課堂教學、學生作業反饋情況說明本節課程較好地完成了教學任務,達成教學目標。 四、“數學抽象”素養在課堂教學中培養的建議 1.教師應嚴格執行新的課程標準(2017版),在平時的教學活動中不斷思考如何進行“數學抽象”素養的培養。 2.學生能力的形成有一個過程,教師應重視這個過程。教學中應該讓學生獲得數學概念和規律,提出數學命題和模型,形成數學方法與思想,認識數學結構和體系。 3.學生應該強化觀察、直觀感知的習慣,鍛煉實際動手操作的能力,養成對某一類問題的歸納總結的習慣,增強對問題、現象敢于質疑的習慣,為抽象思維培養創造所需條件。避免只會解題而不知其所然。 總之,數學抽象是六大核心素養中最重要的,對學生的發展起有極其重要的作用,在新的高考模式下,課堂教學應加強數學抽象素養的養成,不斷提高學生的抽象能力和水平。 [ 參? 考? 文? 獻 ] [1]陶虹萍.探討高中數學概念教學中核心素養培養策略[J].課程教育研究,2019(45):130. [2]羅夢瑋,趙繼源.數學抽象能力發展過程及培養策略探究[J].南寧師范大學學報(自然科學版),2019,36(03):137-143. [3]張金良.解密數學抽象探索教學策略[J].數學通報,2019,58(08):23-26+66. [4]劉洪忠.數學抽象素養的培養在高中課堂教學中的體現[J].延邊教育學院學報,2019,33(04):162-164. [5]孫宏安.數學課程目標芻議——學習《普通高中數學課程標準(2017年版)》[J].中學數學教學參考,2019(22):2-6+30.

