淺談“一題多解”對初中生幾何學習的重要性

戢莎

【摘 要】一題多解能讓幾何學習不再枯燥乏味，能使幾何學習充滿濃厚的趣味性和挑戰(zhàn)性，能讓學生的幾何思維能力有所提升。一題多解也能體現(xiàn)出數學的學科性，能在尊重學生個體差異的基礎上，盡可能滿足學生的多樣化學習需要，能讓學生根據自己的實際，感受不同層次的學科知識。

【關鍵詞】一題多解;發(fā)散思維;多樣化學習

初中數學的重要內容之一——平面幾何，對于大部分初中生來說是一個難點。而讓學生靈活運用各種有關知識，通過各種可能途徑來證明一個幾何命題，既可以使學生思路開闊，又能得到左右逢源的效果。用多種方法解答同一道數學題，不僅能使學生更牢固地掌握所學的數學知識，還能使學生更靈活地運用所學知識。要讓學生通過一題多解，分析、比較各種解法的優(yōu)缺點，找到最佳的解題途徑，從而培養(yǎng)學生的創(chuàng)造性思維能力[1]。如果學生能對一道幾何題進行一題多解，深入思考和研究，總結解題方法，那么其必將受益匪淺。

初一下學期，開始學習全等三角形時，筆者明顯能感受到很多學生產生了畏難情緒，不能記憶基本定理、對圖形的結構理解不透徹、對題目條件和結論分析不到位[2]。筆者便找了一些典型的幾何題讓學生思考如何進行一題多解，并在班上講解，以提高學生的積極性和學習興趣。同時，多種方法的分享，使學生對知識的理解和圖形的剖析更透徹。

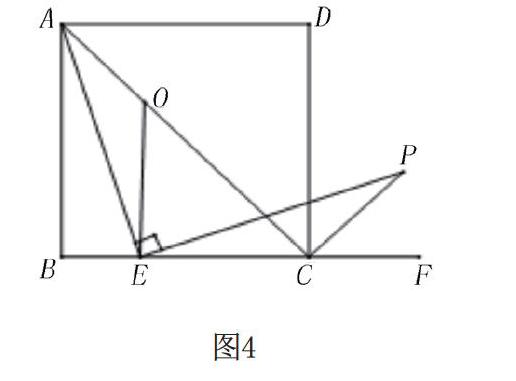
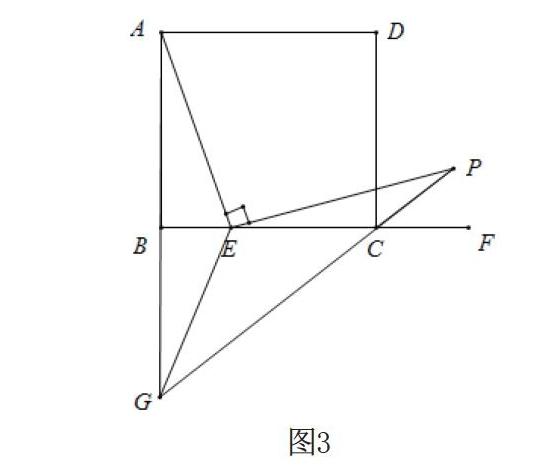
筆者以下面這道題為例，分析其不同解法。

1? ?基于全等三角形的解法

這道題是在初一下學期學習的“全等三角形”中出現(xiàn)，所以學生會想到構造和所在的三角形全等，進而較容易想到在上有，利用“角邊角”證明。

從以上解法可以看出，在初中不同階段對同一個幾何題會有不同解法。隨著數學知識的增加，解題思路會越來越靈活。讓學生采用多種解法解同一道幾何題，能讓學生領會到數學知識之間的聯(lián)系，能讓學生領會到初中數學幾大板塊——代數、幾何、函數之間的聯(lián)系，能增加學生學習數學的興趣，拓展學生思維，使學生不斷提升自己。

【參考文獻】

[1]代國柱.淺談幾何教學中學生解題能力的培養(yǎng)[J].教育，2016（11）.

[2]劉月芳.淺談初中幾何問題的“一題多解”[J].中學課程輔導：教師教育，2015（12X）.