打破常規(guī) 換向思考

陳戀

摘? ?要：逆向思維在物理教學(xué)中存在廣泛的應(yīng)用，在高中物理習(xí)題教學(xué)中，培養(yǎng)逆向思維顯得尤為重要，要培養(yǎng)學(xué)生樂于創(chuàng)新，敢于反其道而行，引導(dǎo)學(xué)生多方面分析問題，促發(fā)反向思考，創(chuàng)造性解決問題。

關(guān)鍵詞：逆向思維;習(xí)題教學(xué);轉(zhuǎn)化互逆

逆向思維是對(duì)司空見慣的似乎已成定論的事物或者觀點(diǎn)反過(guò)來(lái)思考的一種思維方式，是一種敢于發(fā)散、敢于創(chuàng)新的思維方法。敢于“反其道而行”，從問題的相反面深入進(jìn)行思維探索。《道德經(jīng)》也曾提到：“反者道之動(dòng)”，對(duì)立面中往往存在著推動(dòng)事物前進(jìn)的潛在動(dòng)力。物理學(xué)發(fā)展的過(guò)程，也是思維不斷創(chuàng)新和拓展的過(guò)程，從經(jīng)典力學(xué)到量子力學(xué)都告訴我們，跳出常規(guī)的思維模式，轉(zhuǎn)換思維，才能有新突破。德布羅意將波粒二象性移植到實(shí)物粒子中，提出物質(zhì)波的概念;奧斯特的電流磁效應(yīng)這一奇異現(xiàn)象將法拉第深深吸引，更加堅(jiān)定了法拉第的觀點(diǎn)，電與磁之間存在必然的聯(lián)系而且能夠相互轉(zhuǎn)化。電能夠生磁，那么磁也必定能夠生電。無(wú)數(shù)次試驗(yàn)的失敗都無(wú)法打倒他堅(jiān)定的信念，十年的堅(jiān)持最終等來(lái)了電磁感應(yīng)現(xiàn)象的發(fā)現(xiàn)。

物理學(xué)中也存在許多的概念規(guī)律，理解的過(guò)程需要學(xué)生進(jìn)行雙向思維或者多向思維，習(xí)題教學(xué)可以在具體的情境中鞏固物理概念、規(guī)律，更可以學(xué)會(huì)如何去思考和解決相應(yīng)的問題，活化思維模式，提高思維品質(zhì)。不過(guò)，解題過(guò)程中學(xué)生有著思考問題的常規(guī)習(xí)慣，容易造成知識(shí)結(jié)構(gòu)的片面性，面臨某些問題理解時(shí)，正向的探索會(huì)使問題復(fù)雜化，此時(shí)不如從問題的相反方向去思考，換一個(gè)方向想想，問題迎刃而解的同時(shí)也培養(yǎng)學(xué)生的科學(xué)思維能力。對(duì)于同一個(gè)問題進(jìn)行不同方面的思考，從而更好的認(rèn)識(shí)問題的本質(zhì)、內(nèi)在規(guī)律和相互關(guān)系。

1? 時(shí)間反演，過(guò)程可逆

物理現(xiàn)象中存在許多可逆性的過(guò)程，充分利用好這些可逆性，將運(yùn)動(dòng)過(guò)程的最后一秒看成是第一秒，將末狀態(tài)視為初狀態(tài)，不僅可以使解題思路簡(jiǎn)潔便利，降低解題難度，更能主動(dòng)推進(jìn)學(xué)生的逆向思維的培養(yǎng)。

【例題1】質(zhì)點(diǎn)做勻減速直線運(yùn)動(dòng)，在第1s內(nèi)位移為6m，停止運(yùn)動(dòng)前的最后1s內(nèi)位移為2m，求：在整個(gè)減速運(yùn)動(dòng)過(guò)程中質(zhì)點(diǎn)的位移大小。

分析：設(shè)質(zhì)點(diǎn)做勻減速運(yùn)動(dòng)的加速度大小為a，初速度為v0。由于質(zhì)點(diǎn)停止運(yùn)動(dòng)前的最后1s內(nèi)位移為2m，則根據(jù)逆向思維可得：s2=at2，所以a=4m/s2。

質(zhì)點(diǎn)在第1s內(nèi)位移為6m，由s1=v0t-at2得v0=8m/s。在整個(gè)減速運(yùn)動(dòng)過(guò)程中質(zhì)點(diǎn)的位移大小為：s==8m

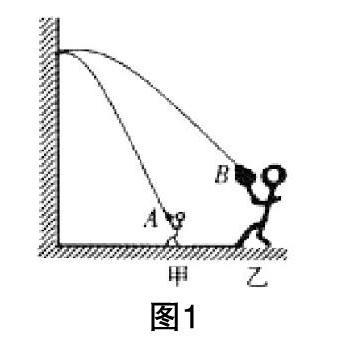
【例題2】?jī)晌煌瑢W(xué)進(jìn)行投籃比賽，如圖1，由于身高和體能的差異，他們分別站在不同的兩處將籃球從A、B兩點(diǎn)投出，兩人投出的籃球都能垂直打中籃板的同一點(diǎn)并落入籃框，不計(jì)空氣阻力，則下列說(shuō)法中正確的是（）

A.甲、乙拋出的籃球從拋出到垂直打中籃板的運(yùn)動(dòng)時(shí)間相等

B.甲、乙拋出的籃球初速度的大小可能相等

C.甲、乙拋出的籃球初速度的豎直分量大小相等

D.甲、乙拋出的籃球垂直打中籃板時(shí)的速度相等

分析：投擲籃球的運(yùn)動(dòng)本為斜拋，逆轉(zhuǎn)過(guò)程來(lái)看，可視為籃球做平拋運(yùn)動(dòng)的逆過(guò)程，平拋的末狀態(tài)即為斜拋的初狀態(tài)。甲同學(xué)的籃球下落高度大，豎直分速度大，下落時(shí)間長(zhǎng)，水平位移小，水平分速度小，根據(jù)矢量求和可知，A點(diǎn)的合速度可能與乙同學(xué)在B點(diǎn)拋出的籃球的合速度大小相等。學(xué)生運(yùn)用起平拋知識(shí)就駕輕就熟，化繁為簡(jiǎn)，一目了然。

除了運(yùn)動(dòng)過(guò)程可以進(jìn)行時(shí)間反演，光路的可逆性，在反射、折射現(xiàn)象中都普遍遵守，作為光線的反演過(guò)程，光的可逆性為解決光學(xué)問題提供了一條重要途徑。

2? 分合得當(dāng)，等效互逆

等效替代的觀念初次接觸便是在力的合成與分解中，力的合成與分解互為逆運(yùn)算，其核心思想便是合力與分力的等效替代關(guān)系。除此之外，運(yùn)動(dòng)的合成與分解，電路電阻的串聯(lián)、并聯(lián)，習(xí)題教學(xué)過(guò)程中我們可以滲入等效替代，運(yùn)算互逆的思想。

【例題3】F1、F2是力F的兩個(gè)分力，F(xiàn)=10N，則F1、F2可能為（? ? ?）

A. 10N、10N? B.15N、15N? C.10N、30N? D. 30N、50N

分析：力的分解具有任意性，10N的力可按照任意情況進(jìn)行分解，分力的大小不容易確定。本題極易讓我們想起來(lái)合力與分力的等效性，分解是合成的逆運(yùn)算，二力合成的最大值和最小值易求得的。因此，只要對(duì)選項(xiàng)中的兩個(gè)力進(jìn)行合成，則很容易就能得出正確選項(xiàng)A、B了。

【例題4】電路中有三個(gè)電阻，R1=10Ω，R2=15Ω，R3=30Ω，將這三個(gè)電阻并聯(lián)在電路中，則并聯(lián)后電阻R為多少？

分析：電阻的并聯(lián)思路簡(jiǎn)單，不外乎運(yùn)用并聯(lián)電路的計(jì)算公式=++

計(jì)算可得R=5Ω，計(jì)算量并不算大，但是粗心的學(xué)生不時(shí)會(huì)出現(xiàn)計(jì)算錯(cuò)誤。如果將問題顛倒過(guò)來(lái)看，進(jìn)行并聯(lián)電路的逆運(yùn)算，R1=10Ω可以視為由3個(gè)30Ω的電阻并聯(lián)而成，R2=15Ω視為由2個(gè)30Ω電阻并聯(lián)而成，電路中總計(jì)由6個(gè)30Ω的電阻并聯(lián)，易得總電阻R===5Ω。

正向求索時(shí)若是山窮水盡，或許分合得當(dāng)，逆向探求會(huì)柳暗花明。

3? 轉(zhuǎn)換角度，化繁為簡(jiǎn)

在力的動(dòng)態(tài)平衡中，學(xué)生接觸得比較多的都是只有一個(gè)變量的情景，若存在兩個(gè)變量，需要學(xué)生具有較強(qiáng)的數(shù)學(xué)功底，能夠?qū)⑽锢砬榫澳Ｐ徒Y(jié)合數(shù)學(xué)知識(shí)進(jìn)行解題，同時(shí)解題中存在的兩個(gè)變量相互關(guān)聯(lián)，增大了解題難度，對(duì)于數(shù)學(xué)基礎(chǔ)一般的學(xué)生來(lái)說(shuō)，存在較大的困難。但是轉(zhuǎn)換角度思考，將兩個(gè)變量為一個(gè)變量呢？

【例題5】（2017年全國(guó)卷I）? 柔軟輕繩ON的一端O固定，其中間某點(diǎn)M拴一重物，用手拉住繩的另一端N，初始時(shí)，OM豎直且MN被拉直，OM與MN之間的夾角為α（α>π/2）。 如圖2，現(xiàn)將重物向右上方緩慢拉起，并保持夾角不變。在OM由豎直被拉到水平的過(guò)程中（? ? ? ）

A.MN上的張力逐漸增大? ? B.MN上的張力先增大后減小

C.OM上的張力逐漸增大? ? D.OM上的張力先增大后減小

分析：在本題中，這個(gè)中間的節(jié)點(diǎn)一共受三個(gè)力，有兩個(gè)力方向發(fā)生改變且二力夾角不變，只有一個(gè)力的大小和方向恒定，這大大提高了解題的難度。其實(shí)我們可以采用逆向思維，把這兩個(gè)力往右方上移是相當(dāng)于把選點(diǎn)下方的重力順時(shí)針轉(zhuǎn)過(guò)來(lái)（如圖3），在這樣的基礎(chǔ)上將兩個(gè)力方向的變化轉(zhuǎn)化成一個(gè)力方向的變化，這就相當(dāng)于成功了一半。根據(jù)三力平衡，兩個(gè)力的合力應(yīng)與第三力等大反向，將OM段的拉力FOM和MN段的拉力FMN方向視為不變，F(xiàn)OM和FMN二力的合力大小為mg ，二力的合力方向從豎直向上順時(shí)針轉(zhuǎn)向水平向右，由圖3可以明顯觀察到，F(xiàn)OM先增大后減小，F(xiàn)MN逐漸增大。同時(shí)由幾何知識(shí)可知，當(dāng)mg⊥FMN時(shí)，F(xiàn)OM最大。

巧用逆向思維，啟發(fā)學(xué)生從不同角度，用不同角度去探求問題結(jié)論，順繁則逆，多向思考，同時(shí)更可以順逆思路結(jié)合，進(jìn)一步提高學(xué)生的分析、歸納、綜合應(yīng)用的能力。

4? 變加為減，推陳出新

【例題6】（2015-2016學(xué)年福建省龍巖市質(zhì)量檢測(cè)卷） 某實(shí)驗(yàn)小組用圖4所示裝置進(jìn)行“探究動(dòng)能定理”的實(shí)驗(yàn)，實(shí)驗(yàn)步驟如下：

（1）掛上鉤碼，調(diào)節(jié)長(zhǎng)木板的傾角，使小車能沿長(zhǎng)木板向下做勻速運(yùn)動(dòng);

（2）保持長(zhǎng)木板傾角不變，打開速度傳感器，取下輕繩和鉤碼，讓小車從長(zhǎng)木板頂端靜止下滑，分別記錄小車通過(guò)速度傳感器1和速度傳感器2時(shí)的速度 v1和v2;

（3）重新掛上細(xì)繩和鉤碼，改變鉤碼的個(gè)數(shù)，重復(fù)1、2的步驟。

分析：在魯科版“探究動(dòng)能定理”的實(shí)驗(yàn)中，往往需要鉤碼拉動(dòng)著小車加速運(yùn)動(dòng)，平衡摩擦力使合外力F合等于繩子拉力T，同時(shí)要求小車的總質(zhì)量遠(yuǎn)遠(yuǎn)大于鉤碼質(zhì)量，才能使繩子拉力近似等于鉤碼的重力，從而使合外力等于鉤碼的重力。但是在學(xué)生實(shí)驗(yàn)中，往往無(wú)法滿足小車的總質(zhì)量遠(yuǎn)遠(yuǎn)大于鉤碼質(zhì)量，實(shí)驗(yàn)誤差較大，學(xué)生在解題過(guò)程中經(jīng)常理解不到位，導(dǎo)致錯(cuò)解。反過(guò)來(lái)想想，何不去掉鉤碼后才讓小車加速下滑，此時(shí)不再需要小車的總質(zhì)量遠(yuǎn)遠(yuǎn)大于鉤碼質(zhì)量，鉤碼的重力就是小車的合外力，化加為減，出奇制勝。

逆向思維有其獨(dú)特的魅力，反其道而行之，跳出常規(guī)，發(fā)現(xiàn)創(chuàng)新。科學(xué)思維方法需要有意識(shí)地進(jìn)行訓(xùn)練，在習(xí)題教學(xué)中培養(yǎng)學(xué)生的逆向思維，引導(dǎo)學(xué)生由此及彼，幫助學(xué)生建立多向思維，舉一反三，培養(yǎng)學(xué)生的思維轉(zhuǎn)換能力，有效培養(yǎng)學(xué)生準(zhǔn)確理解和靈活運(yùn)用物理規(guī)律的能力，讓學(xué)生明確知識(shí)的來(lái)龍去脈和知識(shí)點(diǎn)之間的聯(lián)系，問題簡(jiǎn)單化，創(chuàng)造出意想不到的奇跡來(lái)。