核心素養(yǎng)下的中考數(shù)學命題特點
周忠勇


[摘要]近年來,中考數(shù)學關于核心素養(yǎng)的命題考查頻頻出現(xiàn),關于核心素養(yǎng)的中考數(shù)學命題,最常見的有四種類型:邏輯推理和數(shù)據(jù)分析、數(shù)學文化、實際問題、閱讀和創(chuàng)新,研究此類考題,有助于提高學生的解題能力,有助于改進教師的教學。
[關鍵詞]核心素養(yǎng);中考數(shù)學;命題
[中圖分類號]G633.6[文獻標識碼]A [文章編號]1674-6058(2020)11-0002-02
我們分析了近幾年各地的中考數(shù)學題,發(fā)現(xiàn)關于數(shù)學核心素養(yǎng)的命題有如下幾種類型,
一、重視邏輯推理和數(shù)據(jù)分析的考查
程序框圖和探索規(guī)律是近年中考數(shù)學命題的特點之一,此類題重點考查學生的邏輯推理和規(guī)律探索的能力。
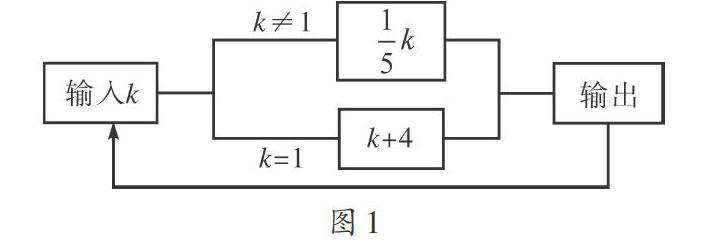
[例1](2018年甘肅中考第18題)如圖1所示,這是一個運算程序示意圖,若第一次輸入k的值為625.則第2018次輸出的結果是____,
解題策略:解這類題,首先要看清程序框圖的結構和執(zhí)行過程,程序框圖共三種結構:①順序結果,從上至下依次執(zhí)行,②選擇結構,根據(jù)判斷框內的條件是否成立,選擇其中一條路徑執(zhí)行,③循環(huán)結構,根據(jù)循環(huán)變量的初始值和終止值,反復執(zhí)行循環(huán)體內的語句,其次,要理解賦值語句,它是把賦值號(=)右邊的值、變量的值或者表達式的值賦給左邊的變量,當左邊變量得到新的值,原來的值自動消失,即用新的值取代了原來的值,最后要按順序寫出執(zhí)行過程,中考數(shù)學題中“選擇結構”的較多,多賦值幾次就能發(fā)現(xiàn)規(guī)律。
二、重視對數(shù)學文化的考查
歷史和文化是我們中華民族的根,也是“立德樹人”的文化基礎,有關數(shù)學文化的考試題目在中考數(shù)學中頻頻出現(xiàn),主要考查方程思想和數(shù)學建模的核心素養(yǎng),弘揚我國數(shù)學發(fā)展史,培養(yǎng)學生的愛國情懷等,
[例2](2018年甘肅中考第21題)《九章算術》是中國古代數(shù)學專著,在數(shù)學上有其獨到的成就,不僅最早提到了分數(shù)問題,也首先記錄了“盈不足”等問題,如有一道闡述“盈不足”的問題,原文如下:今有人共買雞,人出九,盈十一;人出六,不足十六,問人數(shù)、雞價各幾何?譯文為:現(xiàn)有若干人合伙出錢買雞,如果每人出9文錢,就會多11文錢;如果每人出6文錢,又會缺16文錢,問買雞的人數(shù)、雞的價格各是多少?
解題策略:這類題表面上是數(shù)學史方面的考題,考查學生的語文功底,實質是考查方程或方程組方面的知識應用,只要學生讀懂題意,巧設未知數(shù)列出方程或方程組,就可按解方程或方程組步驟來完成解題,
三、重視數(shù)學與實際問題的考查
中考數(shù)學常將實際問題與解直角三角形的應用結合起來,其中實際問題貼近現(xiàn)實生活,這類題主要考查學生的數(shù)學轉化能力和建模思想,體現(xiàn)了數(shù)學的實用性。
解題策略:通過審題,發(fā)現(xiàn)題中有角度值和線段的長度值,就要往解直角三角形方面考慮,將實物圖畫成幾何圖形,再將幾何圖形分割成直角三角形和特殊四邊形(有時需要作輔助線),注意在分割成直角三角形和特殊四邊形時,至少將兩個已知條件放到同一個直角三角形中,這樣有利于計算出其他的邊和角,這些邊和角有助于計算出最終結果,當然有時可以借助方程思想來解題。
四、重視閱讀能力和創(chuàng)新能力的考查
數(shù)學創(chuàng)新題是現(xiàn)在中考數(shù)學的一種新題型,給定一個新模型來創(chuàng)設新的問題情境,要求學生在閱讀理解的基礎上,依據(jù)題中提供的信息,聯(lián)系所學的知識和方法,實現(xiàn)信息的遷移,從而順利地解決問題,這類題具有非完備性、不確定性、發(fā)散性、探究性、層次性、發(fā)展性、創(chuàng)新性等特點。
[例4](2019甘肅中考第27題)閱讀下面的例題及點撥并解決問題:
解題策略:解決這種題應注意三個基本問題:認真審題,確定目標;深刻理解題意;開闊思路,發(fā)散思維,運用觀察、比較、類比、聯(lián)想、猜想等帶有非邏輯思維成分的合理推理,以便為邏輯思維定向,方向確定后,借助邏輯思維,進行嚴格推理論證,其中,讀懂例證是關鍵。

