談初中數學教學中數形結合思想的應用
張飛標

摘?要:隨著我國教育事業的不斷創新和改革,培養學生的綜合實踐能力、邏輯思維能力是初中數學教學的主要核心目標。在初中數學教學的過程中,使用數形結合的方法,能夠有效的培養學生的邏輯思維能力和抽象理解的能力,為學生的數學學習提供積極地幫助作用。本文主要探討了初中數學教學中使用數形結合的方式和應用方法,以期能夠推動初中數學的教學質量。
關鍵詞:初中數學;教學;數形結合;應用
引言:
數學是學生學習生涯中的重要學科。數學學習,主要學習的知識就是各種數字、數學概念、數學定理以及各種幾何圖形的等等。數學作為一門的比較枯燥的知識學科,往往對于初中階段的學生的吸引力較小,學生對數學學習不感興趣。基于此,運用數形結合的方法來進行教學實踐活動,能夠幫助學生將一些抽象的知識點具體化,提升學生對數學知識的理解,進而提升學生的學習質量,培養學生的數學邏輯思維。
一、數形結合思想的概念
數形結合思想是一種數學思想方法。數與形是數學中的最基本的研究對象,它們在一定條件下可以相互轉化。中學數學研究的對象可分為數和形兩大部分,數與形是有聯系的,這個聯系稱之為數形結合,或形數結合。
數形結合的應用大致又可分為兩種情形:一種是借助于數的精確性來闡明形的某些屬性,另一種是借助形的幾何直觀性來闡明數之間某種關系,即數形結合包括兩個方面,第一種情形是“以數解形”,而第二種情形是“以形助數”。
在初中數學教學中,最先接觸的數形結合課程就是數軸,如果教師用“講”的方式向學生灌輸正數、負數、絕對值等等概念,學生對這種抽象的概念很難理解,但是經過用數軸的方式講解,學生就能直觀地理解它的含義和概念,所以數形結合的方法對于學生學習數學知識有著積極地作用。
二、初中數學教學中數形結合思想的應用途徑
學生在小學階段所學習的數學課程中,已經了解和掌握一些簡單的圖形知識,并且對于一些數學教學中所需要的工具如三角板、量角器、直尺等也會進行使用,這些工具也是數形結合思想應用的必備用品。教師在教學中,也可以引導學生從生活的角度利用數形結合的思想,例如,我們生活中常見的籃球、跑道線等等,將這些圖形運用到數學教學中,也就有了數形結合的課程知識。
(一)利用數軸圖形分析代數問題
例如試題:已知a>0,b<0,且-b>a,試比較a,-a,b,-b的大小。
若直接比較上述4個數的大小有一定的難度,若用特殊值法,是可以比較它們的大小關系的,若把它們在數軸上表示出來,利用數軸的直觀性,它們的大小關系將一目了然。
已知a>0,b<0,所以在數軸上表示數a,b的點分別分布在原點的右邊和左邊。
因為-b>a,所以表示數a的點到原點的距離小于數b的點到原點的距離。
所以a.-a.b.-b這四個數在數軸上所排列順序應該是b.-a.0.a.-b(如下圖所示)。
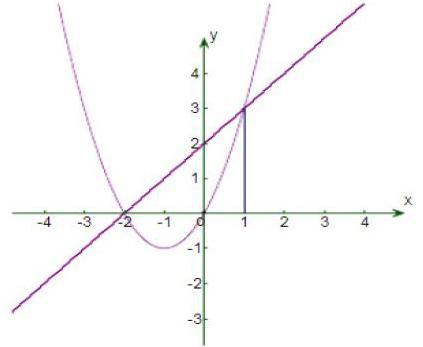
通過數軸上的表示,我們就能直觀的看到b<-a 在教學中,教師要著重向學生進行講解體重的重點問題,數a表示的是實數,可以是正數、可以是0、也可以是負數;不能認為a一定是正數,-a一定是負數。 (二)在數學教學中,學生會接觸到統計學當中的基本的知識點內容,通常我們會在坐標系中將各個數據進行對應的標注,為了剛好的計算出這些數據的中樞、平均數與中位數,還有數據波動產生的方差與標準差,我們就可以利用數形結合思想,通過利用數軸與坐標軸圖形解決統計問題,這樣就可以幫助學生直觀的了解數據的情況和它們之間的關系,為學生的學習起到積極地幫助作用。 (三)數形結合應用于不等式中時:不等式的證明是一個難點,有些題目利用常規的方法難以證明,但是如果不等式具有幾何意義,運用數形結合,問題就會變得簡單。 例:二次函數y=ax2+bx+c和一次函數y=mx+n的圖像如圖所示,則Jax2+bx+c 分析:一次函數圖像是一條直線,經過一、二、四象限,y隨x的增大而增大。二次函數圖像是條拋物線,開口向上。 由圖像的觀察可知:一次函數圖像經過(-2,0),(0,2)兩點二次函數圖像經過(-2,0),(0,0)兩點,對稱軸x=-1.我們可以根據點的坐標分別求出函數的解析式,然后去解不等式組,求出x的取值范圍。這樣可以求出,但運算量較大,而且容易出錯。如果運用數形結合的思想,通過圖像觀察就比較簡單。 所以解題為: 一、當x<-2或x>1時,二次函數的圖像在一次函數的圖像上方,此時ax2+bx+c>mx+n; 二、當-2≤x≤1時,二次函數的圖像在一次函數的下方,此時ax2?+bx+c≤mx+n; 因此所求的取值范圍_2≤x≤1 數形結合是中學數學教師必須掌握的一種數學思想,而且也是為學生提供幫助的一種學習方法,因此在教學中,積極地引導學生運用數形結合思想進行學習和解題,進而提升數學教學的教學質量。 結束語: 數形結合思想能夠幫助學生直觀的理解數學中的抽象概念,提升學生的思維邏輯能力和數學素養,從而快速的解決問題。教師在利用數形結合思想進行教學時,也要根據學生的實際情況來不斷地創新教學方式,最大程度的滿足學生的個體化需求,為培養學生良好的綜合能力奠定堅實的基礎。 參考文獻: [1]初中數學教學中數形結合思想的應用[J]. 周志鵬.?課程教育研究. 2018(50). [2]“數形結合百般好,隔離分家萬事休”——在初中數學教學中活用數形結合思想[J]. 李夢圓,趙澤峰.?才智. 2019(11). [3]滬科版初中數學教學中融入數形結合思想之實踐[J]. 余贊東.?數學學習與研究. 2019(14). [4]初中數學教學中數形結合思想的滲透[J]. 頡瑞紅.?甘肅教育. 2019(16). [5]數形結合思想在初中數學教學中的滲透[J]. 王林.?甘肅教育. 2019(17). [6]數形結合思想在初中數學教學中的應用[J]. 朱春苗.?中國校外教育. 2019(28).

