高考數學核心素養導向的研究
張婷

[摘要]數學核心素養對高考有導向作用,同時,高考也反過來對數學核心素養的落實有積極引導作用.根據《普通高中數學課程標準(2017年版)》中基于數學核心素養的評價框架,分析研究2019年高考全國卷I理科數學中核心素養的構成、試題特點和趨勢,研究發現,基于現行高考的時長和題量,素養分布合理,注重邏輯推理和數學抽象的考查,弱化機械運算,對應用問題的考查不斷提升,增加了開放性問題和探究性問題.
[關鍵詞]高考數學;核心素養;高考;導向
[中圖分類號]G633.6
[文獻標識碼] A
[文章編號]1674-6058(2020)14-0005-03
《普通高中數學課程標準(2017年版)》(簡稱《課標》)全面提出了數學學科的六個核心素養,強調數學教學以發展學生數學學科核心素養為導向,而高考的價值取向是教學的指揮棒,核心素養在課堂中培養還依賴于高考改革.
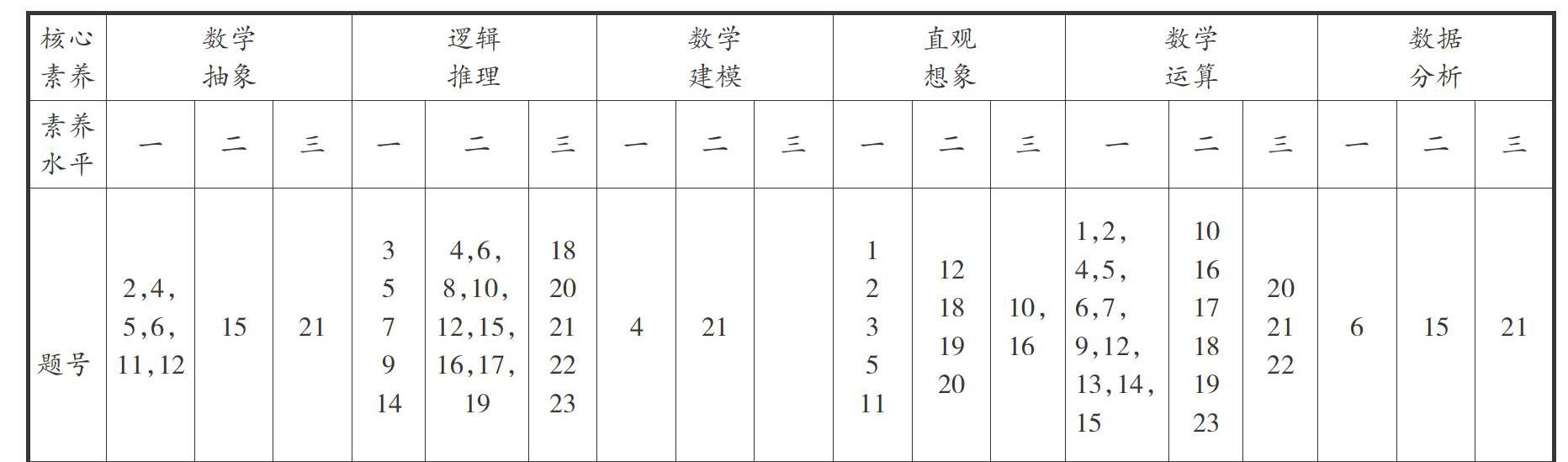
本文以2019年高考全國卷I理科數學為例,探討核心素養對高考數學的導向作用,《課標》根據數學學業質量水平將每個數學核心素養劃分為三個水平,分別是基于高中畢業學業水平考試水平、高考水平、大學自主招生水平,以此為標準,筆者統計了試題中的核心素養的構成及水平,如下表:
一、素養的分布及合理性
試題對于數學運算、邏輯推理的考查力度最大,分別在20道題和19道題中考查,貫穿全卷,而且水平分布合理,數學運算本質上是演繹推理,所以邏輯推理素養與數學運算素養具有很強的相關性,在本卷中,更加注重運算中的邏輯成分,凸顯運算的思維性,淡化機械運算,在第10、16、20、21題的運算中,都要多次確定運算對象,正確選擇運算路徑和設計程序解決問題,考查了各層級的數學運算.
2019年數學考試大綱中有要求:對推理論證能力和抽象概括能力的考查貫穿于全卷,是考查的重點,在本卷中邏輯推理的三個水平的考查符合大綱要求.以演繹推理為主,合情推理在第4題、第21題中有涉及,筆者認為可以增加合情推理的考查,發揮高考的導向作用,數學抽象能力是從具體問題歸納出共性的能力,再把這些共同特征變為解決一類問題的方法,也就是我們說的舉一反三,它是學數學最重要的能力,在試題中共考查7次,以考查在情境中辨析和運用概念的水平為主,無真正意義上從現實情境中高度概括出數學結構或在數學內部做更高層次的抽象的考查,共有11題考查了直觀想象,比較符合數形結合思想在數學中的地位.
數據分析共考查了3次,考查根據現實情境中的數據信息,用概率模型來解決問題,數學建模的考核出現2次,數學建模是考查數學探究、應用和創新能力的很好載體,但基于現行高考的時間與題量,無法實現對數學建模完整過程(思考探究、收集處理數據、建立模型、檢驗模型)的考查,因此在高考中,只能考查部分建模過程——概率模型的建立或探究模型的合理性,如本卷第21題,
二、試題特點與導向
1.穩定創新,立足素養,考查主干知識
本卷對四條主線的主干知識考查穩定,知識結構合理,同時穩中求變,創造性地調整題序,概率統計題在2018年后移至20題,2019年更是首次成為壓軸題,打破固定套路,強調了應用導向,在知識交匯處出題是高考常見出題思路,每年都在突破思維定式,第21題將概率與二階線性遞歸數列結合,反映高考穩定創新的命題特色,對選拔創新人才、抑制題海戰術起到了良好的導向作用,
2.情境多樣,開放探究,釋放改革信號
高考以數學核心素養為導向,穩步變化,試題釋放改革信號.
(1)考查的情境從單一到綜合,從學科知識到真實情境,關注當下,強化數學應用,體現數學的科學和社會價值.
(2)從條件、結論封閉到條件、結論開放型,加強學生創新能力和核心素養的考查.
(3)弱化機械運算,注重思維導向.
(4)挖掘數學經典和文化,涉及黃金分割、隨機游走概率模型等,注重傳承數學文化中包含的數學思想方法,
筆者選擇其中兩道題為例談高考改革的方向.
[例1](理科數學第4題)古希臘時期,人們認為最美人體的頭頂至肚臍的長度與肚臍至足底的長度之比是〔(√5)-1〕/2(〔(√5)-1〕/2≈0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此,此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是〔(√5)-1〕/2.若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26cm,則其身高可能是(? ? ).
A.165cm
B.175cm
C.185cm
D.190cm
分析:以往的高考題用詞嚴謹準確,形成閉環,沒有多余的條件,而本題不管從條件的表達和問法,都具有不確定性,用兩個數據都可以進行估算.然而條件又有偏差,咽喉與脖子、“肚臍至足底”與腿長,有相關性也有差異性,將它們近似等同,可以算得26×(1.618/0.618)2≈178.14,105×1.618≈169.89,該選哪個答案呢?比較下誤差,還是“頭頂至咽喉”與“頭頂至脖子”的誤差更小,因而選擇與之結果更接近的175 cm.該題突出了學科素養導向,考查多種素養,同時,條件與問法的“模糊性”和算法與結論的“開放性”給了考生多角度思考的機會,也是高考走向探究性、開放性的風向標.
[例2](理科第21題)為治療某種疾病,研制了甲、乙兩種新藥,希望知道哪種新藥更有效,為此進行動物試驗,試驗方案如下:每一輪選取兩只白鼠對藥效進行對比試驗,對于兩只白鼠,隨機選一只施以甲藥,另一只施以乙藥,一輪的治療結果得出后,再安排下一輪試驗.當其中一種藥治愈的白鼠比另一種藥治愈的白鼠多4只時,就停止試驗,并認為治愈只數多的藥更有效,為了方便描述問題,約定:對于每輪試驗,若施以甲藥的白鼠治愈且施以乙藥的白鼠未治愈則甲藥得1分,乙藥得-1分;若施以乙藥的白鼠治愈且施以甲藥的白鼠未治愈則乙藥得1分,甲藥得-l分;若都治愈或都未治愈則兩種藥均得0分,甲、乙兩種藥的治愈率分別記為α和β,一輪試驗中甲藥的得分記為χ.
分析:本題對學生而言,閱讀困難,望而生畏.其一是文字量大.本題的字符數達歷年新高,為401個,代表復雜的應用情境;其二是符號化表征,代表抽象的數學結構.第二問的本質是通過二階線性遞歸數列來推導通項公式,實際上本題是隨機游走概率模型,如果理解題意,本題并不難解,而且提供初始項和等比數列的證明,都是提示通項公式的求法,為學生提供腳手架降低了難度.(ii)即是解釋數據、校檢模型,考查數學建模過程中對數學模型合理性的探討.何謂合理?標準是什么?題日當中并沒有明確給出,給了考生充分的答題空間,符合命題開放性和探究性的趨勢.
近年概率統計題的趨勢是減少對數據進行復雜的機械運算,而重點后移,考查數據分析處理的能力,為生產決策問題建立模型,強化數學的應用價值,
三、教學建議
1.追本溯源,重視概念形成過程
開放性與探究性的高考導向,必定不是機械記憶與模仿能夠應對的.“重結論,輕推導”的教學必然使學生知其然而不知其所以然.教師應該花工夫教好概念、規律、原理的推導,把握數學本質,發展學生數學抽象概括和合情推理的能力.
2.評價導向,促核心素養水平達成
在教學選材和試題命制中,研究核心素養的評價框架,除傳統分數外,關注學生素養水平的達成.
3.活學活用,增強數學模型意識
要求學生在復雜的綜合情境中通過新舊知識間的聯系抽象出熟悉的模型,轉化為可解決的問題,如本卷第12題,如果熟悉掌握正三棱錐模型的性質和求三棱錐外接球的幾種模型,構建模型、找準路徑,計算量很小.
4.真實情境,突出數學的文化和應用價值
多選擇來自生產、生活的真實素材來創設情境,加強數學與學生生活經驗的聯系.許多高考題的題根來源于數學史中的經典問題,教師應該多鉆研,提高自身的專業素養.
5.知識整合,深化主題式教學
將關聯的知識組合成具有教學主線的大單元進行教學,進行思維深化和能力提升,培養具備結構化的領域知識和技能的人才.
[參考文獻]
[1]中華人民共和國教育部.普通高中數學課程標準(2017年版)[s].北京:人民教育出版社,2018.
[2]教育部考試中心.2019年普通高等學校招生全國統一考試大綱(理科)[M].北京:高等教育出版社,2018.
[3]《基礎教育課程》編輯部.整體把握課程 抓住數學本質發展核心素養:訪普通高中數學課程標準修訂負責人王尚志[J].基礎教育課程,2018(21):27-31.
(責任編輯 黃桂堅)

