巧用幾何畫板輔助教學突破探究難點

摘 要：新知的學習往往是需要學生經歷知識探究的過程，才能更好地理解、運用。但由于受到各種條件的限制，我們探究的內容總是比較特殊，有限，如何化特殊為一般，化有限為無限，來進一步探究，從而驗證學生的猜想，得出結論呢？幾何畫板具有動態性、任意性、準確性等特點，我們可以借其輔助教學，以突破這一探究難點。

關鍵詞：探究;難點;幾何畫板

“授人以魚，不如授人以漁。”因此對于新知的學習，我們一般都是采用探究的形式，讓學生經歷動手操作、觀察、交流、猜想、驗證、歸納的過程來認識和理解新知。但由于受到各種條件的限制，我們探究的內容總是比較特殊，有限，如何化特殊為一般，化有限為無限，來進一步探究，從而驗證學生的猜想呢？這是探究課的一大難點。我們可以借助幾何畫板輔助教學來突破這一難點。

《幾何畫板》是一款優秀教學軟件，它最大的特點就是動態性，我們可以根據教學內容畫出圖形并拖動鼠標任意改其形狀和位置，讓學生直觀地感受數與形的動態變化關系。同時幾何畫板還有計算、度量等工具，我們可以快速、準確度量圖形的角度、長度、面積，坐標等。因此《幾何畫板》這一軟件為我們提供了很好的探究實踐平臺。

下面我就以《探索正比例函數的圖象及性質》為例，來談談如何運用幾何畫板進行探究學習，并附上探究過程中幾何畫板的相關制圖步驟供更多的老師和學生參考學習。

一、 自主探究，引發猜想

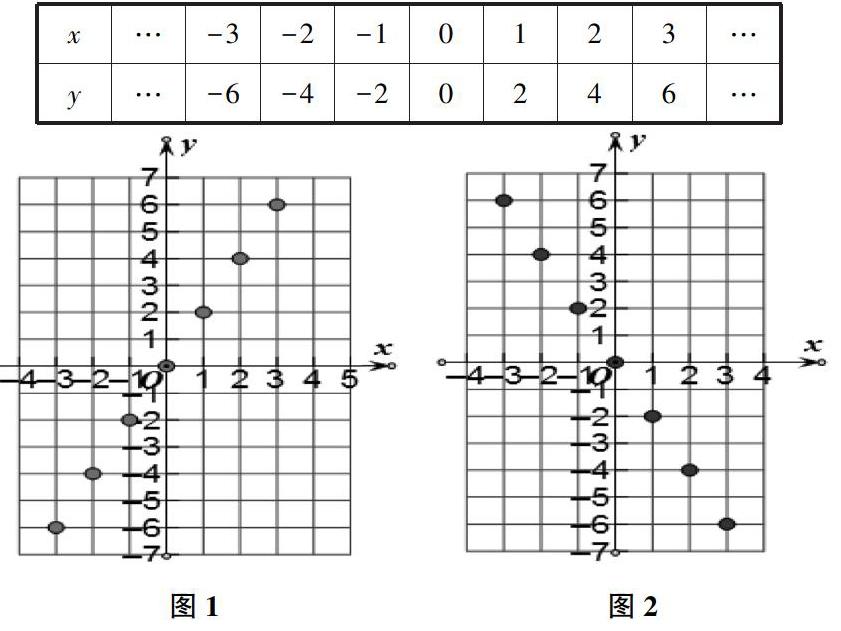
采用問題串的形式先建立函數中x、y的每組值（x，y）與點的對應關系，函數與圖象的對應關系，把數與形聯系起來。再一步步地引導學生列出正比例函數y=2x的七組對應值（如下表），并通過描點、連線的步驟自主探究y=2x的圖象（如圖1），發現這七個點分布在同一條直線上，由此引發猜想1：函數y=2x的圖象是一條直線。

讓學生采用同樣的方法繼續探究函數y=-2x的圖象（如圖2），發現其七個點分布也在同一條直線上，而且兩個圖象有個共同特點都經過原點。由此引發猜想2：所有正比例函數的圖象都是一條直線而且恒過原點。

二、 深入探究，驗證猜想

（一）驗證正比例函數y=2x的圖象是一條直線

七個點不具有說服力，那我們可以取更多的點。我們可以借助幾何畫板“新建參數”“計算”“制表”“描點”等功能，在某個范圍內每格0.5單位或0.1單位，甚至還可更密，快速，準確地描出盡可能多的點（如圖3），讓學生通過這些密密麻麻的點直感地感受地到正比例函數y=2x的圖象是一條直線，從而驗證他們的猜想。

操作步驟：

第一步：制表。①選擇【數據】菜單下的【新建參數】命令新建參數x，初始值設置為-3，再右擊選擇屬性將其數值的精確度改為十分之一，參數的變化范圍改為-3至3，鍵盤調節速度改為0.1單位;②計算2x的值并將其標簽改為y;③選中x，y用【數據】菜單下的【制表】命令進行制表再選擇x與表按住鍵盤上的“+”即可快速算出-3至3這個范圍內所有滿足條件的數對（如圖3中的表）。

第二步：描點。①選擇工具箱中【自定義工具】下的【經典坐標系】中的【螞蟻直角坐標系（無參數版）】新建平面角坐標系;②選中圖3中的表用【繪圖】菜單下的【繪制表中數據】命令，即可描出這些數對所對應的點（如圖3）。

（二）驗證所有正比例函數的圖象都是一條直線

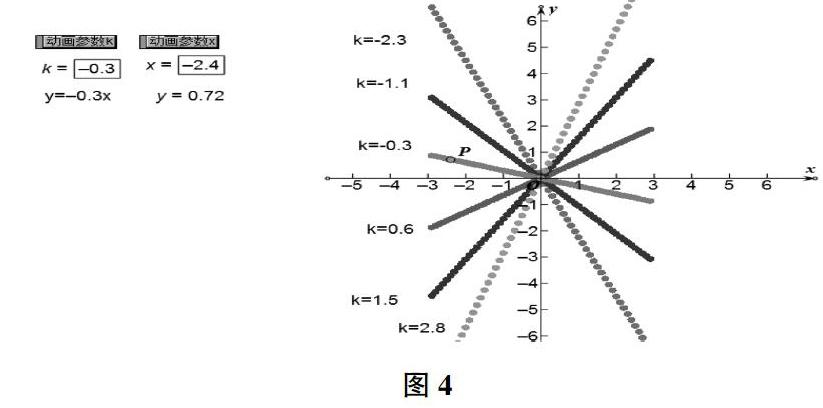
我們可以借助幾何畫板“新建參數”，“操作類按鈕”，“追蹤點”等命令，先新建參數k再利用動畫按鈕隨機確定一個k的值，并繪制動點（x，kx）采用追蹤點的形式，追蹤其在某個范圍內的運動軌跡跡（如圖4），通過這樣的探究方式，學生就能從圖形中直觀地感受到不論k取何值，這些點所形成的軌跡都是一條直線而且都經過原點，從而再次驗證了他們的猜想2。

操作步驟：

第一步：新建參數k。①選擇【數據】菜單下的【新建參數】命令新建參數k;②選中參數k用【編輯】菜單下的【操作類按鈕】命令創建“動畫參數k”按鈕，并將其屬性中改變值的速度和范圍根據自己的需要適當的改變。

第二步：新建參數x。①采用第一步的方法新建參數x（初始值為-3）并創建“動畫參數x”按鈕，設置其屬性;②將“動畫參數x”按鈕的屬性中的動畫方向改為增加并選擇只播放一次，改變數值選擇“離散”。

第三步：追蹤點。①計算kx并將其標簽改為y，選中x和y在建立好的坐標系中繪制點p;②單擊“動畫參數k”按鈕隨機確定一個k值，再選中點p右擊選擇【追蹤繪制點】命令，最后在單擊“動畫參數x”按鈕及可實現追蹤點;③選中點p并右擊【追蹤繪制點】先取消追蹤點p，接著選擇“動畫參數k”按鈕改變k的值，再采用“②的步驟”再次追蹤點p，以此重復，我們就可追蹤不同k值時點p的不同軌跡（如圖4）。

三、 對比探究，感知求異

（一）數形結合，歸納總結y=2x與y=-2x的性質

我們可以借助幾何畫板“創建自定變換”“變換”“操作按鈕”“制表”等命令，在y=2x的圖象上構造一個點M（a，b），并通過變換的功能來實現從左往右拉動點M（如圖5），讓學生從形的角度直觀地感受a，b的變化情況;另外，我們還可通過制表來得到點M在移動過程時點的對應坐標，從數的角度再次驗證形的結論。這樣我們就可將數與形結合起來，讓學生從這兩個角度很好地理解y=2x與y=-2x中y隨x的變化情況，發展學生的幾何直觀并滲透數形結合的思想。

操作步驟：

第一步：畫出函數y=2x的圖象。①選擇【數據】菜單下的【新建函數】命令新建函數y=2x;②創建“螞蟻直角坐標系（無參數版）”;③選擇【經典坐標系】工具中的【函數y=f（x）圖象生成工具（軌跡）】命令再依次單擊x軸，y軸即可畫出y=2x的圖象。

第二步：創建變換，實現形的動態。①在y=2x的圖象上構造點M并分別向x軸，y軸引垂線，垂足的標簽分別設置為a，b;②選中點M和a用【變換】菜單下的【創建自定義變換】命令創建“M→a變換”，再用同樣的方法創建“M→b變換”;③在y=2x的圖象構造線段TM并選中TM執行【變換】菜單下【“M→a”變換】、【“M→b”變換】即可實現通過拉動點M，得到點M，a，b的運動軌跡（如圖5）。

第三步：制表，追蹤點的坐標。①右擊點M顯示其坐標并選中點M的坐標進行制表;②在函數y=2x構造點S，選中M和S用【編輯】菜單下的【操作類按鈕】命令創建“移動M→S”按鈕;③選中表并單擊“移動M→S”按鈕，按住鍵盤中的“+”即可追蹤點M在運動過程中的對應坐標（如圖5中的表）。

第四步：用同樣的方法制圖探究y=-2x的性質。

（二）由特殊到一般，進一步探究y=kx的性質

由上面的探究可知由于y=2x與y=-2x的k互為相反數，其圖象的變化趨勢和性質也相反，那是不是k>0時圖象的變化趨勢都與y=2x相同并具有與它相同的性質，反之與y=-2x相同呢？我們可以借助幾何畫板制作可變函數y=kx（如圖6），通過拉動點k即可改變k的值，學生就能從形的角度直觀地感受到圖象的變化。最后歸納總結函數y=kx圖象的變化趨勢只有兩種，當k>0時同y=2x，當k<0時同y=-2x，從而歸納總結出正比例函數y=kx的性質。

操作步驟：

第一步：制作可變函數y=kx。①采用上面的方法建立直角坐標系，并畫出一條與y軸平行的直線，在其上構造一點其標簽設置為k并度量出k的縱坐標將標簽改為k;②選擇【數據】菜單下的【新建函數】命令新建函數y=kx并采用上述的方法畫出y=kx的圖象（如圖6）。

第二步：上下拉動點k，函數y=kx的圖象就會隨之變化。

由此可見借助幾何畫板輔助教學，可以突破傳統教學中的探究難點。它可以化靜為動，化特殊為一般，化抽象為直觀，將數與形充分結合起來，讓學生更好地理解新知，運用新知。條件允許的話我們還可放手讓學生自己借助幾何畫板進行新知探究，體驗探究的成就感，充分調動他們的學習熱情。

作者簡介：鄒麗琴，福建省漳州市，漳州市第五中學。