小學數學拓展課：設計、樣態、模式與取向

潘紅娟

數學拓展課的開發與實施

數學拓展課，旨在激發數學興趣、關注活動經驗、落實核心素養、實現深度學習。近幾年來，不斷為廣大教師認同、接受。但縱觀此領域的研究可以發現，大部分數學拓展課還是停留于單節課的實踐，缺少從“課”到“類”的研究。杭州市江干區小學數學團隊在經歷區域調研、行動研究之后，進一步由點及面類化梳理，初步形成“數學繪本類”“數學文化類”“數學游戲類”“項目學習類”“綜合實踐類”等各類數學拓展課的基本模型，并就不同課型的教學結構、內容開發、教與學的關鍵把握等進行共性提煉，為數學拓展課的開發與實施提供很有價值的基本參照模式。本刊特刊登其研究成果，以饗讀者。

【摘? ?要】數學拓展課是指以非教材例題為學習內容，以綜合素養發展和活動經驗積累為重點，并將學習內容與數學游戲、數學繪本、數學文化、綜合實踐、真實任務等有機整合的課型。闡述數學拓展課教學設計的內容維度與一般流程，構建數學拓展課的基本樣態與教學模式，可為教師提供拓展課教學的基本結構與范式參照。

【關鍵詞】小學數學;拓展課;教學設計;教學模式

數學拓展課，通常是指以非教材例題為學習內容，以綜合素養發展和活動經驗積累為重點，并將學習內容與數學游戲、數學繪本、數學文化、綜合實踐、現實話題、真實任務等有機整合的課型。

當前，關于數學拓展課的研究，不乏對其價值意義、基本特征的深入研究，不乏對單節拓展課的課例研究。那么，我們能為數學拓展課的教學研究做些什么呢？經過思考，確定了兩個可能的方向：其一，還原數學拓展課的設計原理與基本思路，為一線教師設計數學拓展課提供一般的流程框架與程序參照;其二，從“課”到“類”，對數學拓展課進行分類研究與模式構建，對不同課型的教學結構、教與學的關鍵把握進行共性提煉，為一線教師實施拓展課教學提供一般的實踐路徑與模式參照。筆者所在團隊開發了200余節數學拓展課例，積累了一些經驗。下面從“教學設計”“基本樣態與模式構建”“基本取向”三個維度展開討論。

一、數學拓展課教學設計的內容維度與一般流程

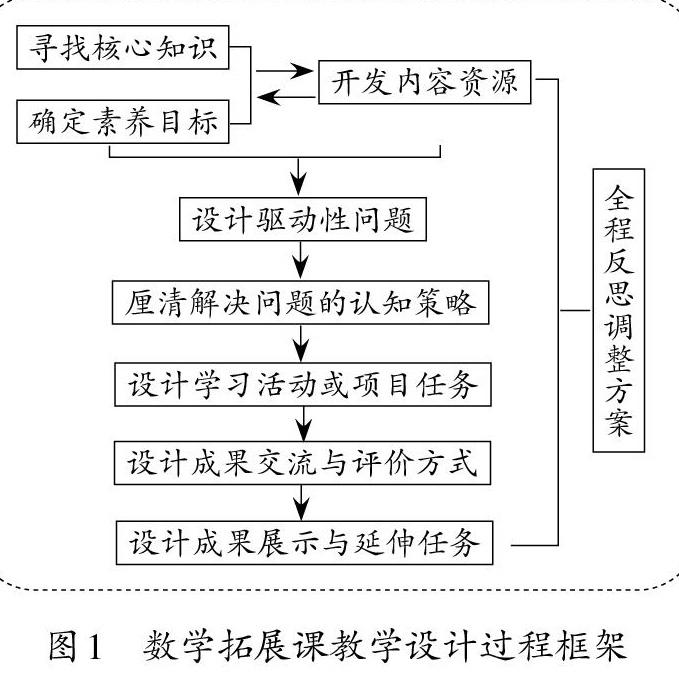
有效設計數學拓展課是實施拓展課教學的前提。實踐中我們逐漸認識到，指向素養的拓展課教學已經大大超出原來基于教材內容的“教學設計”范疇，沒有可依據的明確的教學目標，沒有直接可利用的例題材料與內容，教師在進行設計時需要思考以下八個維度的問題：①學科知識：拓展課教學將指向數學學科的哪些知識與能力？②素養目標：期待學習中培育學生哪些方面的素養？③內容資源：選擇怎樣的內容資源？是某一個熱點話題、某一個游戲、某一本繪本，還是某一個史料？④驅動性問題：采用怎樣的問題驅動學生深度參與學習？⑤認知策略：問題將引發學生采用哪些學習策略？⑥活動任務：設計怎樣的挑戰性任務可以導引學生思考？⑦學習評價：如何設計交流評價活動，以促進成果、方法的共享與提升？⑧成果展示：期待學生產生怎樣的成果或延伸話題？

下面的框架圖（如圖1）大致描述了數學拓展課教學設計的基本流程。

以“小區垃圾知多少”這一內容為例，對以上數學拓展課教學設計過程框架作簡要闡釋。

（1）尋找核心知識，確定素養目標，開發課程內容。數學拓展課教學設計一般有兩條路徑：路徑一，先有課程內容，然后根據內容資源進行教學化處理，確定相應的數學知識能力目標與素養目標;路徑二，先有學習目標，包括數學認知層面的核心目標、需要培養的綜合素養目標，然后去選擇、創生課程內容。兩者都需要教師具有較強的課程開發能力。“小區垃圾知多少”屬于前者，經歷的是內容資源“課程化”的過程。由熱點話題引發，挖掘問題所蘊含的數學性和教育性，據此出發形成拓展學習課程。

（2）設計驅動性問題。驅動性問題是拓展課教學設計的關鍵，直接與整節課的目標指向、學習策略、學習方式相關聯。“垃圾問題”可涉及的話題眾多，如“垃圾分類問題”“垃圾存放問題”“垃圾處理問題”等等。最后我們選擇“一個小區一天會產生多少垃圾”作為驅動性問題，主要考慮幾方面因素：①這一問題具有數據分析能力、運算能力、解決問題能力等極為豐富的能力培養要素;②這是一個熱點話題，具有鮮明的“環境保護”教育性特征;③學生已有知識基礎、經驗儲備可支持此問題研究;④問題解決的空間較大，解決策略多樣。

（3）厘清解決問題的認知策略。設計教學活動之前，教師需要分析學生是如何解決這個問題的，學生所用到的是低階學習策略還是高階學習策略。事實上，解決“小區垃圾知多少”的問題，首先，學生需要開展調查，可以“按戶調查”“按人調查”“按單元調查”“按幢調查”等;其次，調查方式多種多樣，可以向社區咨詢、官網查詢、調查問卷、實地入戶等;最后，問題解決的結果也可不同，可以用“重量”“體積”等方式進行垃圾量的表征。顯然，整個問題的解決，學生所用到的策略不是低階學習層面的信息加工，而是高階學習層面的推理、分析、問題解決、實驗、調查等。

（4）設計學習活動或項目任務。學習活動的設計直接指向學習過程。“小區垃圾知多少”的任務設計，經歷了從“提供調查數據—計算垃圾量—體驗垃圾量的多少”到“方案設計—方案論證—實踐研究—成果交流”的轉變。學習任務的轉變，實現了從“解題計算”到“問題解決”的轉型。為更好地發揮“任務單”的導引作用，教師在項目任務單中，設置了“研究主題”“總體思路”“研究步驟”“可能遇到的困難”等具體內容，讓學生經歷研究者必須思考的步驟與問題。

（5）設計成果交流與評價方式。無論哪一種數學拓展課，在學生經歷探索之后，如何進行交流、分享與評價，都應該成為該課教學設計的重要內容。教師需要從以下幾方面進行先期設計：①設計交流方式。是口頭匯報、操作演示、PPT匯報，還是視頻演示？②設計交流順序。是并列式交流，還是遞進式交流？是每個小組逐一匯報，還是將同類研究的小組整合匯報，其余小組補充？③設計交流側重。每一個成果交流指向問題解決的同時，是否有不同的價值？一方面，考慮匯報者解決問題策略的不同;另一方面，考慮不同小組的匯報能否對此問題的研究方法、研究過程、研究結果等作方法層面的引導。例如，教師在設計“小區垃圾知多少”的小組交流時，有意識地選擇不同的側重點，如“方案設計的完整性”“樣本選取的合理性”“計算方法的巧妙性”“計算結果的體驗性（所產生的垃圾量究竟有多少）” 等，并根據側重點逐一進行評點與強化，實現方法策略引導。④設計評價維度。為避免匯報時平面陳述與淺層重復，教師可以設計評價視角：“請你給匯報小組的過程、方法、結果找找亮點，并找找茬。”通過評價，尋找優點、提出質疑、給出建議。指向“亮點”與“建議”的評價，有效凸顯解決問題的過程方法與策略取向。

（6）設計成果展示與延伸任務。教師在拓展教學設計之初就需要規劃：期待學生產生怎樣的學習結果？成果要點有哪些？用怎樣的方式呈現？例如“小區垃圾知多少”案例，課中，成果以PPT、微視頻形式，通過演講在全班進行展示。課后，成果以海報、小電影等方式在學校展示。在被調查的社區，通過小區電子屏、海報等方式進行成果展示與“減少垃圾產生，做好垃圾分類”的宣傳。

二、數學拓展課的基本樣態及模式構建

以一節課、一個項目為切入點展開實踐與思考，雖能促進教師對這節課的深入研究，但“就課研課”的形式，認識往往會停留于“只見樹木，不見森林”的層面。因此，我們有意識地從“課例研究”轉向“課型研究”，試圖對拓展課的基本樣態進行分類，讓每一節拓展課與某一類基本課型或課型變式相對應。通過同類課例的比較、類化與提煉，形成一類課的基本模式。

（一）數學拓展課教學模式提煉的一般過程

之所以提煉數學拓展課的教學模式，是因為模式具有較好的“框架功能”和“程序功能”。框架功能，可以使教師更好地把握教學活動整體及各要素之間的關系;程序功能，則可以更好地反映某一類拓展課的環節、進程與結構，使其更具操作性。

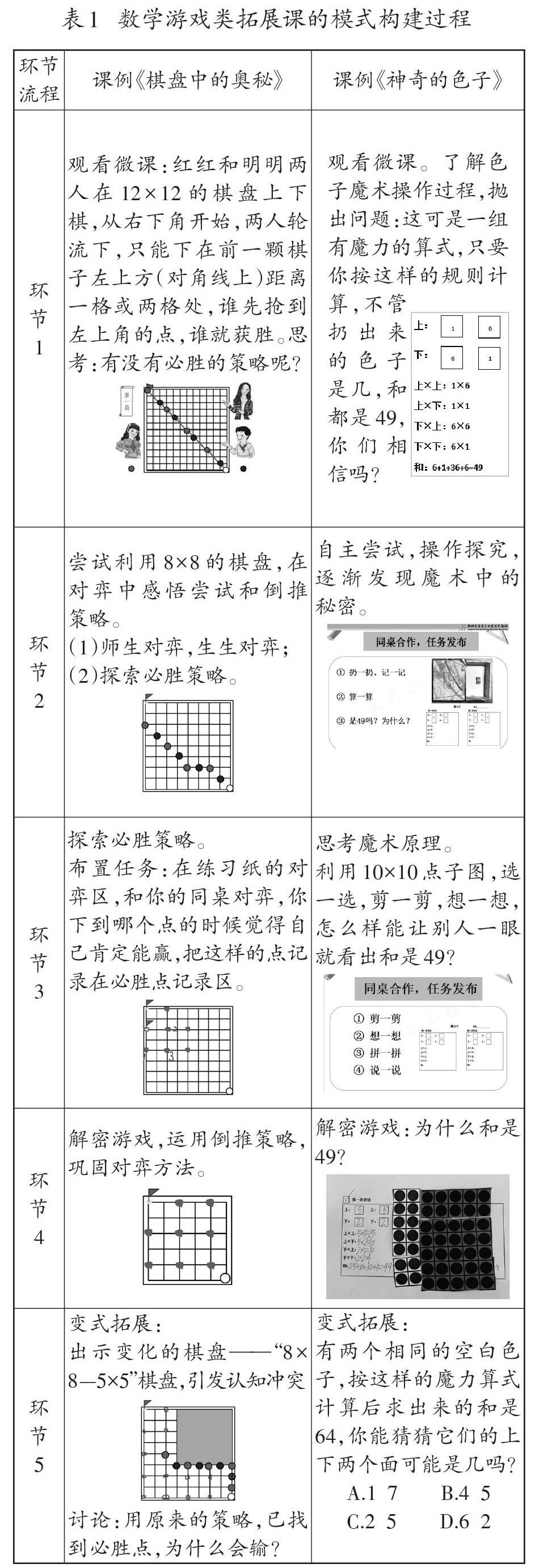
下面以“棋盤中的奧秘”與“神奇的色子”為課例基礎，呈現數學游戲類拓展課的模式構建過程（如表1）。

1 觀看微課：紅紅和明明兩人在12×12的棋盤上下棋，從右下角開始，兩人輪流下，只能下在前一顆棋子左上方（對角線上）距離一格或兩格處，誰先搶到左上角的點，誰就獲勝。思考：有沒有必勝的策略呢？

2 嘗試利用8×8的棋盤，在對弈中感悟嘗試和倒推策略。

（1）師生對弈，生生對弈;

（2）探索必勝策略。

3 探索必勝策略。

布置任務：在練習紙的對弈區，和你的同桌對弈，你下到哪個點的時候覺得自己肯定能贏，把這樣的點記錄在必勝點記錄區。

4 解密游戲，運用倒推策略，鞏固對弈方法。

5 變式拓展：

出示變化的棋盤——“8×8-5×5”棋盤，引發認知沖突

討論：用原來的策略，已找到必勝點，為什么會輸？ 變式拓展：

有兩個相同的空白色子，按這樣的魔力算式計算后求出來的和是64，你能猜猜它們的上下兩個面可能是幾嗎？

A.1? 7? B.4? 5

C.2? 5? D.6? 2

通過以上案例比較，大致可以得出游戲類拓展課的基本模式與操作要點（如圖2）。

當然，以上僅是對游戲類拓展課一般模型的提煉，不同的游戲內容仍會有不同的結構變式。在把握游戲類拓展課基本教學流程的同時，教師仍然有必要進一步思考這類課的其他問題，例如：如何處理好游戲的“熱情參與”與“理性思考”之間的關系？如何處理好“知識運用”與“關鍵能力”的整合？如何處理好“游戲挑戰性”與“游戲可接受性”之間的關系？等等。

（二）各樣態拓展課的基本模型與操作要點

每一節數學拓展課往往具有各自的特征，很難清晰分類與界定，為便于描述，我們暫將拓展課教學分為“數學游戲類”“數學繪本類”“數學文化類”“綜合實踐類”“項目學習類”“熱點話題類”等。在各樣態模式研究的過程中，每一類均經歷了“課堂實踐”“分類比照”與“模式構建”的過程（如表2）。

形成一類樣態的基本模式，其優勢是適用性廣泛，易在不同情境、不同主題下遷移應用。但值得說明的是，不同內容、不同主題的同類課并非具有十分統一的結構，每一個樣態的基本模型背后，一定會有若干種變式，限于篇幅，不再展開。（部分拓展樣態的案例支持與具體模式，可見本期話題后續文章）

三、關于數學拓展課教學的基本取向

（一）追求“數學認知”與“綜合目標”的有機整合

數學拓展課并不滿足于知識技能的獲取、記憶與固化，“學科育人”是數學拓展課的立意之本。那么，定位于整體素養的發展，是不是可以不依托于數學認知呢？我們以為，基于學科的拓展課，仍應追求“整體發展”與“學科認知”兩者的和諧生長，而不是脫離于數學認知與思維提升虛空發展，部分課例的目標分析列舉如表3。

[拓展課例 數學認知目標要點 其他素養目標要點 《彩虹糖里的數學》（一年級）

【驅動性問題】

估一估120g彩虹糖有幾顆 ①100以內數的數數

②量感的建立

③估算意識

④“每份數×份數=總數”的關系運用 ①實驗操作的能力

②“普通定樣法”“工具定樣法”“二分法”和“份數法”等解決問題策略 《漂亮的三角形》（二年級）

【驅動性問題】

閱讀繪本，創造三角形;給繪本中的三角形分類;欣賞繪本中的密鋪美麗圖案，分析三角形拼組 ①三角形的穩定性

②三角形的特征與分類

③通過三角形的拼組體會“密鋪”原理

④多邊形認識初步滲透 ①閱讀興趣的激發

②閱讀方法的指導

③信息獲取能力

④交流表達能力

⑤創新能力 《探索人體的表面積》（六年級）

【驅動性問題】

測量人體的表面積 ①表面積的意義

②平面組合圖形的面積計算，圓柱、長方體的表面積計算

③平均數的統計意義

④樣本的科學性

⑤統計圖表的制作分析 ①問題解決能力

②小組合作能力

③演講表達能力

④質疑批判能力

⑤利用社會資源能力 《一卷膠帶有多長》（六年級）

【驅動性問題】

想辦法知道一卷膠帶有多長 ①鞏固圓的特征

②鞏固圓周長計算和圓環面積計算

③以小估大、排水法等策略 ①方案的設計、實施與反思

②體驗解決問題的多樣策略 ]

以上案例的基本思想是著眼于綜合素養，堅守學科特質，將“數學認知目標”融于“整體育人目標”中，這應該是數學拓展課的基本取向。

（二）驅動性問題要蘊含豐富的探究性與驅動力

驅動性問題，應該是數學拓展課學習的核心要素。問題設計要蘊含豐富的實踐探究性和驅動力，有利于學生通過問題，進行操作嘗試、小組合作，發展深度思維。

表3所列案例中，“估一估120g彩虹糖有幾顆”“閱讀繪本，創造三角形”“測量人體的表面積”“想辦法知道一卷膠帶有多長”等驅動性問題，可以是一個真實項目，可以是一個游戲任務，可以是綜合實踐活動，也可以是繪本閱讀中的體驗活動。這些問題，大多具備以下特點：能較大程度地激發學生興趣;與數學知識具有一定的關聯性;問題非常規，不易完成;讓學生產生小組合作的想法，以便完成任務并取得成功;問題的解決具有一定的空間。

以《探索人體的表面積》為例，實踐活動的成功開展，取決于教師選擇一個好的驅動性問題：“你會求人體的表面積嗎？”問題一經產生，豐富而巧妙的解決策略相應誕生。這個成功拓展案例的驅動性問題具有怎樣的特征呢？①情境性。對此情境學生感興趣，但幾乎沒有嘗試過。②復雜性和挑戰性。沒有直接可利用的公式、方法與步驟，具有極強的探索性。③可接受性。“表面積”的概念，“求不規則圖形的面積”“求長方體、正方體、圓柱表面積”等知識經驗，可支持問題解決。④開放性。解決問題策略空間大，“描輪廓法”，將不規則轉化為規則;“裹紗布法”“穿睡衣法”，將曲面轉化為平面;“直接測量法”，通過圓柱、長方體公式直接計算求得;“查資料法”，幫助學生形成信息獲取的意識與能力。

（三）讓高階學習帶動低階學習

高階學習是一個有意義運用知識的過程，包含六個方面的高階策略：問題解決、創見、決策、實驗、調研和系統分析。要判斷數學拓展教學中學生的學習質量，可以看這個學習過程中學生是否運用了這些策略。如果在拓展教學中，一個高階學習策略都找不到，僅僅停留于信息收集、組織、儲存、鞏固等低認知策略運用，那么這樣的數學拓展課便不是我們所要倡導的。

“垃圾中的數學問題”大量運用了問題解決策略;“單車中的數學問題”主要采用了調研策略;“一卷膠帶有多長”主要采用了實驗策略，“我是‘毅行設計師”主要采用了創見策略，學生將發散性思維運用于毅行方案設計中;“棋盤中的奧秘”采用了決策策略;“給杭州市汽車車牌編號”采用了系統分析策略……當然，很多時候的問題解決，認知策略運用并不是單一的，往往會互相關聯，協同運用。

參考文獻：

[1]夏雪梅. 項目化學習設計：學習素養視角下的國際與本土實踐[M].北京：教育科學出版社，2018.

[2]斯坦，等.實施初中數學課程標準的教學案例[M].李忠如，譯.上海：上海教育出版社，2000.

[3]加涅，等.教學設計原理[M].王小明，等譯.上海：華東師范大學出版社，2018.

[4]邵漢民. 由“課例研究” 到“課型研究”[J]. 教育理論與實踐，2017（32）.

（浙江省杭州市江干區教育發展研究院? ?310020）