數學拓展：開展數學深度學習的有效路徑

陳惠芳

摘 要：?教材是呈現數學知識的重要載體，是傳遞數學思想和方法的主要路徑。如果我們在解讀教材例題、分析課后習題時，適時進行數學拓展，延長學生的學習視線。那么，無疑會幫助學生聚焦核心知識，促進學生深度學習。讓學生優化認知結構，建立數學模型，豐厚數學活動經驗，掌握解決問題的路徑和方法，從而提高分析問題和解決問題的能力和水平。

關鍵詞：數學拓展;深度學習;數學思維

關于深度學習的理解，黎加厚教授認為：“深度學習是在理解學習的基礎上，學習者能夠批判性地學習新的思想和事實，并將它們融入原有的認知結構中，能夠在眾多的思想間進行聯系，并能夠將已有知識遷移到新的情境中，做出決策和解決問題的學習。”在小學數學教學中，我們要適時進行數學拓展，延長學生的學習視線，幫助學生聚焦核心知識，促進學生深度學習。

一、從例題處拓展，由“定數”到“變數”，優化認知結構

很多教師認為“教材無非是個例子”。但是，從教學實踐看，蘇教版小學數學教材是由一大批數學專家、數學名師精心編撰而成的，教材選用多少個例題、多少個習題，安排什么內容的思考題等，都是經過認真研究、反復權衡的。因此，教材是呈現數學知識的重要載體，也是傳遞數學思想和方法的主要路徑。對教材所選用的例題，我們決不能簡單處理，既不能按部就班地簡單教學，也不能“視而不見”，隨便更換教材例題，而應該在認真解讀教材的基礎上，以教材為藍本，進行精加工，讓例題由薄變厚，幫助學生不斷優化認知結構。

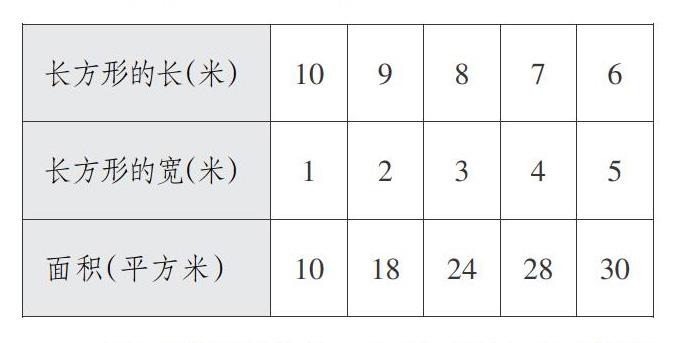
例如：蘇教版小學數學教材五年級上冊用“一一列舉”的策略解決實際問題（如上圖），筆者教學時采用了以下四個步驟，對例題進行了適度拓展。

1.問題導學，自主學習。教師要求學生獨立思考：王大叔用22根1米長的木條圍一個長方形花圃，怎樣圍面積最大？

2.分享交流，有序思考。教師先邀請幾個學生上臺，分享自己的想法，進行反饋，并通過比較突出有序思考，做到不重復不遺漏。

3.數形結合，尋找規律。教師出示課件，幫助學生理解怎樣通過一一列舉的方法，找到長方形的長與對應的寬，求出這個花圃的面積（如下表）。教師讓學生觀察：有什么發現？

[長方形的長（米） 10 9 8 7 6 長方形的寬（米） 1 2 3 4 5 面積（平方米） 10 18 24 28 30 ]

通過數形結合，比較觀察，初步得出：長方形的周長一定時，當長與寬越接近，長方形花圃的面積越大。

4.適度拓展，變式練習。王大叔用24根1米長的木條，靠一面墻圍成一個長方形花圃，想一想，怎樣圍面積最大？（長與寬取整米數）

[長方形的長（米） 22 20 18 16 14 12 10 8 6 4 2 長方形的寬（米） 1 2 3 4 5 6 7 8 9 10 11 面積（平方米） 22 40 54 64 70 72 70 64 54 40 22 ]

教師組織學生認真觀察：現在又有什么發現？

相互交流后，有的學生開始質疑：現在怎么不是“長與寬越接近時，長方形花圃面積越大”？

教師組織學生進行兩種情況的比較，再次觀察。

學生交流后得到：當周長一定，一面靠墻時，如果長是寬的2倍，花圃的面積最大。

基于上面的教學思考，可以發現，教師從教材出發，進行適當的拓展訓練，在用一根定長的線段圍一個長方形時，有可能直接圍成幾個不同的長方形，這時“長與寬越接近，面積越大（正方形面積最大）”，而用這根定長的線段一面靠實物（墻壁）去圍不同形狀的長方形時，“長是寬的2倍時，面積最大”。這樣的比較觀察、探索發現，由淺表的學習轉向深層理解，幫助學生充分掌握一個面積最大的長方形的內在規律，而不是簡單地得出一個規律，從而豐富了教材內涵，幫助學生主動優化認知結構。

二、從例題處拓展：由“個”到“類”，建立數學模型

縱觀蘇教版小學數學教材，每一個例題所承載的知識點，都是按照一定的學習規律、邏輯規律，從易到難，呈螺旋上升的趨勢。在教學時，教師不妨從例題延伸開去，拓展相關內容，把一個個的知識點整合成一類知識點，從而建立數學模型，幫助學生打破思維定式，深入理解和掌握知識，培養學生靈活運用知識的能力，提高學生分析問題和解決問題的能力和水平。

例如：教學蘇教版小學數學五年級下冊“列方程解決實際問題”時，教師分四個層次進行教學。

1.問題導學，自主學習。借助導學單，學生獨立完成第1題和第2題。

2.交流助學，揭示主題。學生利用舊知，獨立解答上面兩道題。相互交流后，教師出示學生改編題：一輛客車和一輛貨車同時從相距540千米的兩地出發，相向而行，經過3小時相遇。客車的速度是95千米/時，求貨車的速度是多少？有的學生改編的是：求客車的速度是多少？

教師啟發學生利用線段圖來理解題意，找出題中的數量關系，獨立解答。

教師啟發引導學生觀察改編的題目：它們所求問題各不相同，但什么沒有變？

教師進一步追問：這3個題目，除了數量關系相同，它們還都是同時出發，最后都是相遇，但現實生活中所有的行程問題一定都是同時出發、相向而行嗎？最后都是相遇的嗎？

3.改編例題，深化理解。教師出示下面一組題，不計算，觀察思考。

（1）一輛客車和一輛貨車同時從相距540千米的兩地出發，相向而行。客車的速度是95千米/時，貨車的速度是 85千米/時。幾小時后兩車相距360千米？

（2）一輛客車和一輛貨車同時從相距540千米的兩地出發，相向而行。客車的速度是95千米/時，貨車的速度是 85千米/時。幾小時后兩車還相距360千米？

（3）一輛客車和一輛貨車同時從相距540千米的兩地出發，相向而行。客車的速度是95千米/時，貨車的速度是 85千米/時。幾小時后兩車又相距360千米？

通過題組的形式，教師讓學生觀察、比較、發現，這3道題有什么相同之處，有什么不同之處？列的方程式是一樣的嗎？從而進一步理解行程問題的特點，掌握它們的解題規律。

4.由“個”到“類”，順利建模。在此基礎上，教師出示下面幾道習題，不要求學生計算，讓他們列出方程式即可。

（1）媽媽買了一些蘋果和梨，一共用去20元，蘋果4千克，每千克3元，梨2千克，每千克多少元？

（2）小張和小李用25分鐘合打了一篇6000字的稿件，小張平均每分鐘大約打130個字，小李平均每分鐘大約打多少個字？

（3）李大伯用64米長的籬笆圍了一個長方形的菜地，如果這塊菜地的長是19米，那么，它的寬是多少米？

學生交流后，教師要求他們再次觀察：它們有什么相同的地方？

漸漸地，學生發現，這些題目里所講的事情，打字、圍長方形、買蘋果和梨……雖然與行程問題好像無關，但是透過現象看本質，其實它們都是行程問題衍生出來的子問題。 因此，從例題處拓展，通過回顧舊知—提出問題—嘗試探究—觀察比較—反饋建模—符號表示，可以提煉出“行程問題”這一類題的基本解題模式：甲路程+乙路程=總路程，或者（甲速+乙速）×相遇時間=總路程。

更為一般地，從小學一至六年級的學習內容來看，像這樣從教材例題出發，由“個”到“類”，建立數學模型的類型還有很多。這樣從“同一類型組合”的拓展延伸，既增加了教材例題在單元教學或者整本書教學中的分量。而且，有層次的拓展練習有助于學生去情境化，摒棄非本質屬性，聚焦知識本源，從點狀思維到類狀思維，積累了豐富的數學活動經驗，溝通前后知識之間的聯系。

三、從例題處拓展，由“一”生“三”， 發展數學思維

建構主義認為，學習不僅僅是知識的傳遞，而且是學習者建構自己知識經驗的過程，這種建構是通過新舊知識經驗之間的雙向的、反復的相互作用而實現的。在傳統的數學課堂中，對于新課學習，教師總習慣于例題教學—模仿練習—鞏固深化—布置作業。學生熟悉了這樣的套路，久而久之，對新課的學習也就索然無味。可喜的是，新課改背景下越來越多的教師通過認真研讀教材，跳出了原有的教學框架，創設有效的教學情境，設計了富有挑戰性的探究任務，由“一”生“三”，讓學生在課堂上開展深度學習，有力地促進了數學思維的發展。

例如，一位教師在復習蘇教版數學六年級上冊“分數、百分數應用題”時，先出示“解決問題的策略”中的一道例題：

星河小學美術組男生人數占總人數的[25，]已知女生人數為21人，男生有多少人？

教師先讓學生回顧舊知，思考問題：解決分數、百分數應用題時，可以分哪幾步進行？要注意些什么？教師依次板書：理解題意—分析數量關系—列式解答—檢驗，寫上答句。

接著，學生用已有的知識經驗來解決問題，然后小組同學進行交流。教師選擇幾個學生上臺講解，讓學生說一說運用了哪些策略來進行解答。

從學生分享的作品中（圖略），我們可以看到，大部分學生采用了畫圖的策略來做，有一部分學生用轉化的策略來做，還有一部分學生用方程來做。觀察比較后，教師追問：我們在解決分數、百分數的實際問題時，究竟選擇怎樣的策略比較好呢？

學生獨立思考，師生一起梳理，解決分數、百分數應用題時，我們可以根據題目所呈現的信息，靈活選擇解題策略列式解答。接著，教師又出示了下面一組題：

（1）學校六年級生物小組養了120只黑兔，是白兔只數的[45]，白兔養了多少只？

（2）學校六年級生物小組養了120只黑兔，白兔的只數是黑兔只數的1.25倍（125%），白兔養了多少只？

（3）學校六年級生物小組養了一些白兔和黑兔，黑兔與白兔只數的比是4∶5，黑兔是120只，白兔養了多少只？

學生在解答這組題時，一方面重溫了小學階段學過的解決問題的“畫圖、列表、轉化”等不同策略;另一方面，在六年級的復習課中，教師沒有進行題海戰術，而是讓學生認真比較這組題的不同之處，進行解題后的反思。有的學生認為，平時解決問題時，我們要認真看清條件和問題的表述，有的題目表述不同，其實意思是一樣的;有的學生認為，選擇什么策略，應該從簡單的想起;有的學生認為，同一個題目，無論條件多么復雜，關鍵要找到對應的等量關系，再選擇適當的策略解答。

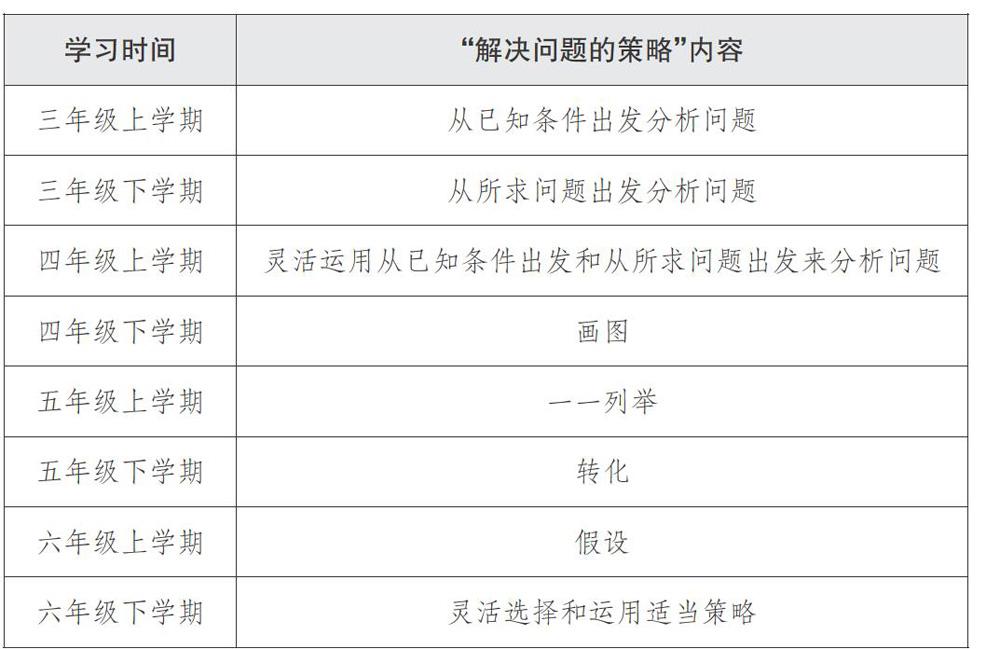
從上面的教學設計流程來看，教師從教材例題處拓展開來，利用題組練習，幫助學生認真梳理蘇教版小學數學從三年級到六年級所涉及的解決問題的相關策略（以2019年為例），如下表所示。

[學習時間 “解決問題的策略”內容 三年級上學期 從已知條件出發分析問題 三年級下學期 從所求問題出發分析問題 四年級上學期 靈活運用從已知條件出發和從所求問題出發來分析問題 四年級下學期 畫圖 五年級上學期 一一列舉 五年級下學期 轉化 六年級上學期 假設 六年級下學期 靈活選擇和運用適當策略 ]

可見，這樣的復習教學，有效促進了學生與學生之間的對話，幫助學生自覺反思策略形成過程，對解決問題采用什么策略進行深度研究，幫助學生由“一”生“三”，引導學生在舉例、畫圖、列表等不同策略的比較中，實現數學學習從“知其然”到“知其所以然”的提升，更重要的是，讓學生豐富解決問題的學習經驗，深度體悟解決問題的數學思想和方法。

當下，培育和發展學生的學科關鍵能力，提升學生的學科素養成為一線教師的追求。教學中，我們要從教材出發，認真研讀，多元解讀，從教材例題處適度拓展，優化、組合、重構、創生學材。教師還要優化課堂教學結構，突出核心內容，真正站在學生的角度來思考教學，激發學生的學習興趣，讓學生體驗解決問題的多樣性和豐富性，變枯燥的知識學習為主動的探究行動，并形成不同層次的數學思考力，提升學習力。

（作者單位：江蘇省張家港市梁豐小學）