基于建構主義的逆矩陣教學設計與實踐

詹環 陳平 夏靜

摘? 要：針對逆矩陣教學中重計算、輕思想的問題，結合建構主義教學理念，在教學中分析學生已有的知識結構，從逆矩陣的幾何背景的角度引入定義，注重逆矩陣與其相關知識點的聯結，利用數學軟件開展教學拓展，培養學生抽象思維能力和解決實際問題的能力。

關鍵詞：建構主義;逆矩陣;教學設計

中圖分類號：G642? ? ? ?文獻標志碼：A? ? ? ? ?文章編號：2096-000X（2020）27-0119-03

Abstract： In order to solve problems of emphasizing calculation and neglecting thought appearing in reverse matrix teaching， construtivism theory was utilized toanalyze cognitive structure of students， inverse matrix was introduced from the point of view geometric， the connection between the inverse matrix and its related knowledge was focused， mathematics software was used to expand teaching tocultivate the students' ability of abstract thinking and the practical problems-solving.

Keywords： constructivism; reverse matrix; teaching design

線性代數是工科各專業的必修課，它主要研究有限維線性空間及其線性映射的理論課程，廣泛應用于自然科學和工程技術工作領域中，具有較強的抽象性和邏輯性[1]。矩陣的逆是矩陣的一種基本運算，它是解線性方程組、矩陣方程的基本工具，也是研究線性逆變換、坐標逆變換以及矩陣相似變換的基本手段。由于有些教師在講逆矩陣知識點的過程中，偏重于逆矩陣判定條件以及計算涉及的公式技巧，對于逆矩陣產生背景、蘊含的逆變換思想方法直接舍棄或者一句帶過，導致學生只是對逆矩陣的定義及計算死記硬背，缺乏對逆矩陣的幾何意義的認識，很難將逆矩陣靈活應用于解決實際問題。

建構主義理論是由瑞士心理學家皮亞杰提出的，建構主義認為學習不是一個被動的接受過程， 而是一個主動的建構過程，不能從教師通過“刺激反應”遷移到學生，而必須基于學生對知識的體察，從自身經驗的反省，與環境，包括與他人的交流中主動地建構起來[2]。建構主義要求教學以學生為中心，根據學生已有的認知結構精心設計教學情景，激發學生的學習興趣，達到使學生建構知識的目的。本文從圖形的幾何變換引入逆矩陣的定義，讓學生明白學習逆矩陣的緣由，隨后在逆矩陣習題設置中強調了逆矩陣和逆變換的意義，通過經濟學中的實例對逆矩陣教學進行拓展，使學生掌握利用矩陣的逆進行逆變換的思想，最后借助思維導圖幫助學生建構系統的知識體系，符合學生的認知規律。

一、學情分析

建構主義要求教師根據學生已有的知識水平創設符合教學內容要求的情境，設計問題引起學生的思考和討論，使得學生有意識地對習得的知識進行建構，所以教師必須了解學生已有的知識和所學的專業，避免教學內容前后脫節。教學中應盡量選取貼近學生生活的實例為教學內容做鋪墊，線性代數是以線性方程組與矩陣為主線的學科，學生已經掌握了矩陣的加法、減法、乘法運算以及相應的矩陣變換，學生自然會產生疑問矩陣有沒有除法？矩陣乘法的逆運算應如何定義？

二、創設情境，引入定義

教師如果完全按照教材先給出一個抽象的線性變換，然后寫出對應的矩陣方程再求逆變換，這種不直觀的引入逆矩陣的教學方式容易讓學生感覺到迷惑。隨著計算機科學技術的發展，計算機圖形學的應用領域越來越廣，圖形的幾何變換，包括圖形的平移、旋轉、放縮等，是計算機圖形學中經常遇到的問題[3]。一個平面的圖形在計算機上存儲為頂點的集合，通過畫出頂點，并將頂點用直線相連即可得到圖形。用矩陣表示圖形的頂點的集合，則平面圖形的平移、旋轉、放縮都可用矩陣乘法實現，以圖形的旋轉變換為例引入逆矩陣的定義。

例1設一個圖像A由11個點連接填充構成，它的位置用一個2×11矩陣表示，頂點的橫坐標儲存在矩陣的第一行，縱坐標儲存在矩陣的第二行，A從X的位置逆時針旋轉90°得到Y，其中

Y=0 -14 -14? 0 0 -11 -6 -6 -4.5 -4.5 00? 4? ?6? 10 8? 5? 3.5 6.1 6.5? 3.2? 2，問圖像原來位于何處？

解：將點P（x，y）逆時針旋轉？漬得到P1（x1，y1），則旋轉變換為x1=xcos？漬-ysin？漬y1=xsin？漬+ycos？漬令R=cos？漬 -sin？漬sin？漬cos？漬，則點的旋轉變換可以用矩陣乘積Rxy=x1y1表示，則圖像A逆時針旋轉90°可表示為Y=0 -11? 0X，已知Y求X。

求解圖形旋轉變換的原圖問題就轉化為解矩陣方程RX=Y，學生容易根據已有的知識聯想到借助解一元線性方程y=ax的思路來解決這個實際問題。對于y=ax，當a≠0時，可解出x=a-1y。對于矩陣也存在類似的運算，自然想到是否可以把RX=Y中的旋轉變換矩陣R移到等式另外一邊，得到旋轉逆變換，即X=R-1Y。由此引入逆矩陣的概念。

定義1[4]對于n階矩陣A，如果存在n階矩陣B，使得AB=BA=E，則稱矩陣A是可逆的，并稱B為A的逆矩陣，簡稱逆陣。

根據逆矩陣定義，當矩陣可逆時，由旋轉變換等式RX=Y容易得到圖像復原等式X=R-1Y。利用實例引入逆矩陣的定義強調了逆變換思想的形成過程，與建構主義的教學理念一致，重視了數學概念的來源，揭示了逆矩陣的本質。

三、數形結合，闡述定理

建構主義認為，為了讓學生了解知識產生的來龍去脈，積極地參與到知識形成的過程中去，要求教師根據教學內容特點合理設置問題協助學生完成對新知識的意義建構。從心理學角度出發，人對圖表的記憶力會比單純的文字強很多，圖形能更好的表達數學概念和定理的意義，在逆矩陣教學中可以設置可視化例題。

顯然，只需要將壓縮的圖像的橫坐標拉伸5倍即可恢復圖像，即該壓縮變換有逆變換。學生容易找到

矩陣C=1 00 0代表圖像變換x1y1=1 00 0xy，即x1=xy1=0，從幾何圖形上可知該變換不可逆，由矩陣定義也可以驗證C=1 00 0無逆矩陣。

根據例2可知不是所有的矩陣都可逆，由此引入逆矩陣的判定條件。

定理1[4]若矩陣A可逆，則|A|≠0。

由例2矩陣B行列式不為零，矩陣B可逆;矩陣C行列式為零，矩陣C不可逆，這進一步驗證了定理1的正確性。數學家華羅庚曾說過：“數缺形時少直覺，形少數時難入微。數形結合百般好，割裂分家萬事非。”將逆矩陣教學應用于實例，并將知識點盡量可視化可以提高教學效果。

四、結合數學軟件，思維拓展

美國在1990年提出了線性代數改革的建議中要求線性代數教學要從具體例子引出概念和理論，計算機技術必須要應用到線性代數教學中[5]。逆矩陣與圖像處理有著密切的聯系，借助matlab求解得到原圖像所對應矩陣

建構主義要求教師在教學中不僅要體現主導作用，更要發揮學生的主觀能動性。組織學生們進行協作性學習，使得學生在探究性學習中發現規律，糾正和補充對所學內容的認識。在研究多個經濟部門之間的投入與產出關系時， W. Leontief教授提出了投入產出模型，我們將下面的“投入產出問題”作為習題， 要求學生獨立思考，完成解答。

練習[3]：某地有一座煤礦， 一個發電廠和一條鐵路， 經成本核算， 每生產價值1元錢的煤需消耗0.3元的電; 為了把這1元錢的煤運出去需花費0.2元的運費; 每生產1元的電需0.6元的煤作燃料; 為了運行電廠的輔助設備需消耗本身0.1元的電， 還需要花費0.1元的運費; 作為鐵路局， 每提供1元運費的運輸需消耗0.5元的煤， 輔助設備要消耗0.1元的電. 現煤礦接到外地6萬元煤的訂貨， 電廠有10萬元電的外地需求， 問： 煤礦和電廠各生產多少才能滿足需求？

五、構建思維導圖，梳理知識體系

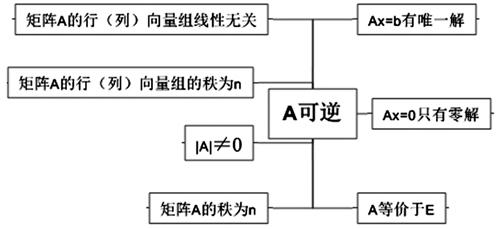
逆矩陣的定義以及計算是線性代數中的重要知識點，通過逆矩陣的學習，學生能夠容易記住判定逆矩陣的條件以及逆矩陣計算公式，但是學生容易“只見樹木，不見森林”。建構主義認為認知結構是將已認識的知識組織起來的心理系統，借助于樹型特別是網狀結構將相互聯系的知識點按照某種關系進行歸類和組合，可以對認知結構進行“擴容”，提高學習效率[6]。思維導圖可以將細碎的知識以簡單的形式有組織有次序的表達出來，為了讓學生清晰掌握逆矩陣的地位作用，結合思維導圖來幫助學生理解逆矩陣與線性代數中知識點的聯系，避免讓逆矩陣教學內容與其它內容脫節，逆矩陣思維導圖見圖3。

六、結束語

在逆矩陣教學中，不僅僅要求學生掌握基本的計算，更重要的是培養學生數學思維的方法，提高學生的工程實踐能力。在工科背景下建構主義教學理念的指導下，結合實例把逆變換的幾何背景引入到各個知識點中，把抽象問題形象化，使學生在形和數的統一中進一步體會到逆矩陣概念的內涵和外延，利用數學軟件結合經濟案例進行探究性學習，借助思維導圖幫助學生建立一個系統、交叉的知識體系。真正建立價值塑造、能力培養、知識傳授三位一體的教育模式有效提高教學質量。

參考文獻：

[1]張肇熾，徐仲.代數與幾何基礎[M].北京：高等教育出版社，2003：7-36.

[2]何克抗.建構主義——革新傳統教學的理論基礎[M].北京：北京師范大學出版社，1999：26.

[3]陳懷琛，高淑萍，楊威.工程線性代數[M].北京：電子工業出版社，2007：157-158.

[4]同濟大學數學系.工程數學線性代數[M].北京：高等教育出版社，2014：42-50.

[5]陳懷琛.實用大眾線性代數[M].西安：西安電子科技大學出版社，2019：1-2.

[6]王龍.建構主義教學觀與文科高數教學[J].黑龍江高教，2008（8）：163-165.