搭建中職生理解函數(shù)概念的橋梁

曹娟

摘要：針對中職學(xué)生理解函數(shù)概念時(shí)存在較大難度的問題，筆者認(rèn)為建立相關(guān)的橋梁很重要。這個(gè)橋梁的一頭是明悉初中函數(shù)的基本知識(shí)，另一頭是凸顯高中函數(shù)的鮮明特點(diǎn)。復(fù)習(xí)初中函數(shù)概念時(shí)，強(qiáng)化函數(shù)表現(xiàn)形式中的解析式法，淡化函數(shù)的不給出具體解析式的抽象形式，完善學(xué)生的認(rèn)知結(jié)構(gòu);學(xué)習(xí)高中函數(shù)概念時(shí)，突出其與初中函數(shù)的異同點(diǎn)，增強(qiáng)學(xué)生的辨識(shí)度。從初中和高中兩頭發(fā)力，教與學(xué)才能發(fā)揮出最大效能。

關(guān)鍵詞：中職生? 函數(shù)概念? 橋梁

對于中職生來說，挖掘數(shù)學(xué)學(xué)習(xí)潛力需要建立一座便于通行的橋梁。讓這座橋梁真正起到使學(xué)生消除畏難思想、樂于全力以赴的作用，我認(rèn)為可以從基本點(diǎn)、閃光點(diǎn)、特異點(diǎn)三個(gè)方面入手。簡言之，基本點(diǎn)是指帶領(lǐng)學(xué)生走出基本概念的盲區(qū)，閃光點(diǎn)是指善于發(fā)現(xiàn)學(xué)生的比較優(yōu)勢，特異點(diǎn)是指通過變式等方法識(shí)別近似內(nèi)容的差異點(diǎn)。

數(shù)學(xué)函數(shù)概念的學(xué)習(xí)是高中生的一大痛點(diǎn)。高中函數(shù)概念和初中函數(shù)概念相比有三個(gè)轉(zhuǎn)折點(diǎn)，即常數(shù)到變量的轉(zhuǎn)折，靜態(tài)到動(dòng)態(tài)的轉(zhuǎn)折，一元到二元的轉(zhuǎn)折。眾所周知，常數(shù)是靜態(tài)的知識(shí)，變量是動(dòng)態(tài)的知識(shí)，幫助中學(xué)生把靜態(tài)的感性認(rèn)識(shí)上升為動(dòng)態(tài)的理性認(rèn)識(shí)，把對一元的認(rèn)識(shí)上升到對二元的認(rèn)識(shí)甚至多元的認(rèn)識(shí)，一直以來都是教師孜孜以求的目標(biāo)。本文擬從以下幾方面談?wù)勛约旱淖龇ā?/p>

一、中職生學(xué)習(xí)函數(shù)概念出現(xiàn)的問題

由于文化課基礎(chǔ)薄弱，很多中職生早已淡忘了初中函數(shù)概念，甚至根本就不懂函數(shù)知識(shí)，一提函數(shù)就有一種模模糊糊、說不清楚的感覺，僅會(huì)舉出常見的函數(shù)表達(dá)式，如y=2x、y=x+2x+1、y=1/x，也就是說他們將函數(shù)概念具體化，具體成函數(shù)表達(dá)式，弱化或淡忘了函數(shù)的本質(zhì)屬性（對應(yīng)關(guān)系），而高中函數(shù)概念恰恰是在保留函數(shù)本質(zhì)屬性的基礎(chǔ)上，推廣函數(shù)概念，所以中職學(xué)生自主學(xué)習(xí)函數(shù)概念時(shí)就會(huì)出現(xiàn)舊傷未愈新傷又來的雙難局面。

二、影響中職生理解函數(shù)概念的因素

首先，是函數(shù)概念本身的原因。“變量”的動(dòng)態(tài)性，函數(shù)關(guān)系的兩元性，呈現(xiàn)形式的多樣性，以及函數(shù)符號(hào)的抽象性都比較難懂。

其次，是學(xué)生認(rèn)知水平不足的原因。理解力達(dá)不到，不能把文字語言、符號(hào)和圖形相互轉(zhuǎn)換;思維水平低，學(xué)生的認(rèn)知結(jié)構(gòu)中數(shù)與形、動(dòng)與靜基本分離，不善于運(yùn)用思維去理解運(yùn)動(dòng)變化的現(xiàn)象;抽象與具體的辯證認(rèn)知不一致，從而難以理解函數(shù)的概念。

三、幫助中職生理解函數(shù)概念的方法

（一）抓住基本點(diǎn)，講清初中函數(shù)概念

1.強(qiáng)化函數(shù)關(guān)系式法，消除抽象性對學(xué)生的負(fù)面影響

函數(shù)表達(dá)式是學(xué)生接觸最多、記憶最牢，又是函數(shù)關(guān)系具體化的一種形式，能夠具體地反映變量間的依賴關(guān)系，這也是學(xué)生為什么一提函數(shù)便會(huì)舉出函數(shù)表達(dá)式的原因。因此，我們遵循認(rèn)知規(guī)律，從學(xué)生角度出發(fā)，強(qiáng)化了列函數(shù)表達(dá)式的過程，讓學(xué)生充分感受到函數(shù)表達(dá)式與方程的相似之處，感受變量間的等量關(guān)系;強(qiáng)化求函數(shù)值的過程，讓學(xué)生充分感受求函數(shù)值與求代數(shù)式值的相同之處，借等量關(guān)系理解對應(yīng)關(guān)系。這樣把前后知識(shí)貫通起來，能夠完善學(xué)生的知識(shí)結(jié)構(gòu)，有效地消除抽象性對學(xué)生學(xué)習(xí)函數(shù)的影響。

如給出兩個(gè)量x和y，當(dāng)x=1時(shí)，y=2;當(dāng)x=2時(shí)，y=4，當(dāng)x=3時(shí)，y=6，當(dāng)x=4時(shí)，y=8…依此類推，學(xué)生自然會(huì)推出y=2x（一次函數(shù)）;給出兩個(gè)量x和y，當(dāng)x=1時(shí)，y=1;當(dāng)x=2時(shí)，y=4;當(dāng)x=3時(shí)，y=9;當(dāng)x=4時(shí)，y=16…依此類推，學(xué)生也會(huì)得出y=x2（二次函數(shù)）;倍數(shù)、平方、倒數(shù)關(guān)系，學(xué)生已經(jīng)熟悉，易于掌握，又能體現(xiàn)一元到二元的轉(zhuǎn)變，具體地反映函數(shù)關(guān)系，有效克服了抽象理解函數(shù)的難題。

2.強(qiáng)調(diào)變量，鞏固變化意識(shí)

簡單的數(shù)據(jù)不能使學(xué)生有效理解變量的概念，不利于學(xué)生變量意識(shí)的形成，因此要繼續(xù)向?qū)W生補(bǔ)充熟知的具體實(shí)例，如下所示。

問題1：我們以100米/分的速度騎車去郊游，那么行駛的路程s與時(shí)間t之間的關(guān)系是_________。

（1）這個(gè)問題中有哪幾個(gè)量？

（2）根據(jù)關(guān)系式填寫下表。

問題2：電影票單價(jià)10元/張，票房收入y元與x張售票張數(shù)的關(guān)系式_________。

（1）這個(gè)問題中有哪幾個(gè)量？

（2）根據(jù)關(guān)系式填寫下表。

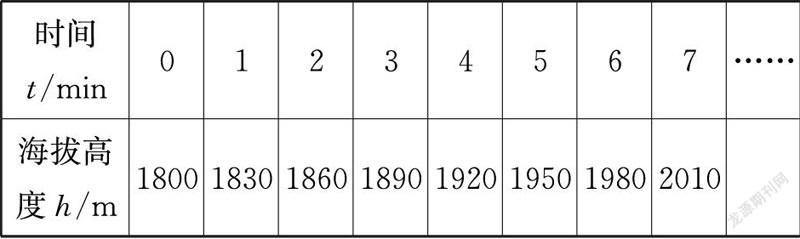
問題3：從1800米處放飛熱氣球，在一段工作時(shí)間內(nèi)，它勻速上升，所到達(dá)的海拔高度h與以及上升時(shí)間t，如下表：

（1）這個(gè)過程中，有哪幾個(gè)量？

（2）熱氣球平均每分鐘上升的高度是多少？

（3）列出氣球高度h與時(shí)間t之間的關(guān)系式。

通過以上三個(gè)問題找量，回憶了變量和常量的概念;通過填表初步回憶了變量間的對應(yīng)關(guān)系。

3.強(qiáng)調(diào)對應(yīng)關(guān)系，抓住函數(shù)本質(zhì)屬性

函數(shù)還有一個(gè)重要屬性——對應(yīng)關(guān)系，因此還要培養(yǎng)學(xué)生把注意力從數(shù)量關(guān)系轉(zhuǎn)移到對應(yīng)關(guān)系上，在表達(dá)關(guān)系式和填表格的基礎(chǔ)上，繼續(xù)引入初中教材里的“用電負(fù)荷曲線圖”，并提出用電負(fù)荷與時(shí)間的關(guān)系，提醒學(xué)生函數(shù)概念強(qiáng)調(diào)的是對應(yīng)關(guān)系，而不是單一的數(shù)量關(guān)系，關(guān)系式只是函數(shù)的表達(dá)形式之一，而不是函數(shù)的屬性，從而全面揭示出函數(shù)的本質(zhì)屬性。

（二）發(fā)現(xiàn)閃光點(diǎn)，歸納函數(shù)概念要素

對于比較簡單的知識(shí)，如果學(xué)生能理解清楚就應(yīng)當(dāng)作為閃光點(diǎn)，及時(shí)表揚(yáng)、鼓勵(lì)學(xué)生。比如引導(dǎo)學(xué)生分析以上幾個(gè)案例，歸納函數(shù)概念要素。相比之下，盡管有不同的表現(xiàn)形式，但它們都具有共同的特點(diǎn)：一是存在兩個(gè)變量;二是兩個(gè)變量之間，有一種對應(yīng)關(guān)系;三是每給定一個(gè)變量的值，根據(jù)對應(yīng)關(guān)系，就確定了另一個(gè)變量（借助列出的等式，由求代數(shù)式的值體現(xiàn)出來，對應(yīng)關(guān)系具體化）。

（三）突出特異點(diǎn)，對比高中函數(shù)概念

對初中函數(shù)概念的全面復(fù)習(xí)，提高了學(xué)生認(rèn)識(shí)函數(shù)的能力，為介紹高中函數(shù)概念鋪設(shè)了一個(gè)臺(tái)階，讓高中函數(shù)概念的產(chǎn)生有了依據(jù)，讓學(xué)生的知識(shí)結(jié)構(gòu)形成鏈條。因此，我們提出從集合的角度出發(fā)，去理解函數(shù)，展示高中函數(shù)概念，將其與初中函數(shù)逐條進(jìn)行對比分析。

（1）自變量取值范圍為數(shù)集D，即把自變量的取值范圍可以看成一個(gè)集合。

（2）按照某個(gè)對應(yīng)法則f，常見的是y=2x，y=1/x，y=x2+2x+1，即初中的函數(shù)關(guān)系式。

（3）y=f（x）即關(guān)系式通常寫成f（x）=2x，f（x）=1/x，f（x）=x2+2x+1

以上分析成功地指出了初中函數(shù)概念與高中函數(shù)概念的異同點(diǎn)：相同點(diǎn)是函數(shù)的本質(zhì)屬性沒變（兩個(gè)變量與對應(yīng)關(guān)系），不同點(diǎn)是函數(shù)符號(hào)改變了。

當(dāng)然，對于這樣比較抽象、難度又大的問題，需要老師充分發(fā)揮自己的主導(dǎo)作用，將內(nèi)容分解，降低難度，適當(dāng)提示學(xué)生，給學(xué)生鋪設(shè)臺(tái)階，給予學(xué)生幫助。

總之，我們要借助于列方程來列函數(shù)關(guān)系式，強(qiáng)化函數(shù)關(guān)系的具體形式，淡化函數(shù)概念的抽象形式，借求代數(shù)式的值求函數(shù)值，體現(xiàn)對應(yīng)關(guān)系，完善學(xué)生知識(shí)結(jié)構(gòu)，以有效消除抽象性對學(xué)生學(xué)習(xí)的影響;借助于初中函數(shù)概念來介紹高中函數(shù)概念，使前后知識(shí)貫通起來，實(shí)現(xiàn)降低學(xué)習(xí)難度、增強(qiáng)識(shí)別度的教學(xué)目的。

參考文獻(xiàn)：

課程教材研究所，中學(xué)語文課程教材研究開發(fā)中心.義務(wù)教育課程標(biāo)準(zhǔn)實(shí)驗(yàn)教科書教師教學(xué)用書[M].北京：人民教育出版社，2007.

責(zé)任編輯：黃大燦