基于數學核心素養的高中教學實踐研究

陳婉玲

[摘 ?要] 以“三角函數”的教學為例，探究如何尋找數學課堂教學中培養核心素養的“生長點”.文章對課程標準的要求進行了分析，在此基礎上提出以“合理情境”來培養抽象思維素養;以“探究性活動”來培養直觀想象素養;以“變式訓練”來培養創新能力;以“歸納提煉”來培養歸納概括素養.

[關鍵詞] 數學核心素養;三角函數;培養;新課程理念

在不斷呼喚新課程改革的當下，課堂教學需擺脫傳統教學中的“知識本位”和“教師本位”，讓數學核心素養在教學實踐的過程中自然落地. 由于數學核心素養具有“隱性”的特質，從而其發展需要內化在課堂教學之中自然滲透，這就需要我們在教學實踐中時時刻刻關注到核心素養的落實，真正意義上尋找能培養核心素養的“生長點”. 本文以“三角函數”一節的部分教學片段為例，探究如何尋找數學課堂教學中培養核心素養的“生長點”.

以“合理情境”來培養抽象思維素養

在傳統教學中，教師常常直接拋出定義，并以例題分析與講解加以鞏固而了事，從而使得教學效果不佳. 新課改風向標下，如何創設情境促使學生自主建構？如何培養學生的數學抽象素養？這些都需要教師獨具匠心地進行教學設計，讓課堂引入具有自身的特色和亮點，讓探究活動順理成章地自然展開，達到培養抽象素養的目的[1].

【教學片段1】

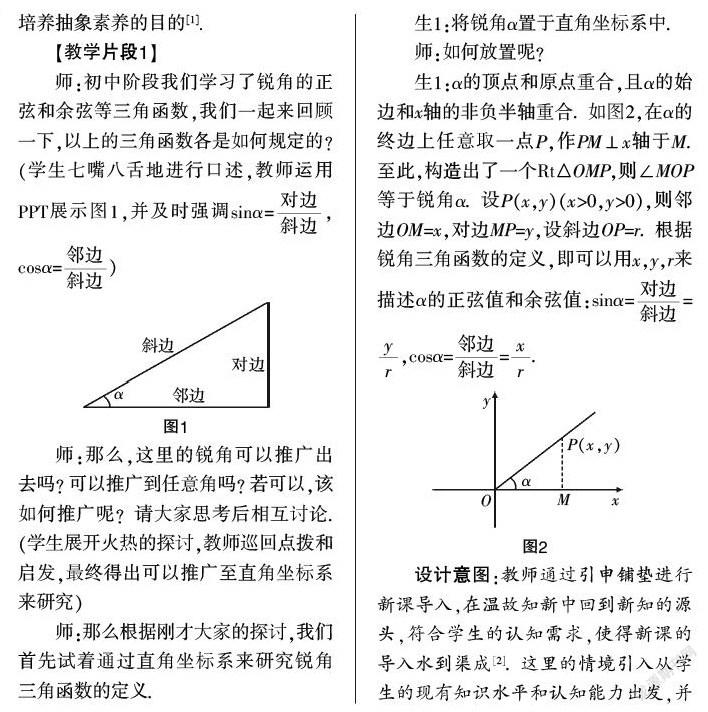
師：初中階段我們學習了銳角的正弦和余弦等三角函數，我們一起來回顧一下，以上的三角函數各是如何規定的？（學生七嘴八舌地進行口述，教師運用PPT展示圖1，并及時強調sinα=，cosα=）

師：那么，這里的銳角可以推廣出去嗎？可以推廣到任意角嗎？若可以，該如何推廣呢？請大家思考后相互討論.（學生展開火熱的探討，教師巡回點撥和啟發，最終得出可以推廣至直角坐標系來研究）

師：那么根據剛才大家的探討，我們首先試著通過直角坐標系來研究銳角三角函數的定義.

生1：將銳角α置于直角坐標系中.

師：如何放置呢？

生1：α的頂點和原點重合，且α的始邊和x軸的非負半軸重合. 如圖2，在α的終邊上任意取一點P，作PM⊥x軸于M. 至此，構造出了一個Rt△OMP，則∠MOP等于銳角α. 設P（x，y）（x>0，y>0），則鄰邊OM=x，對邊MP=y，設斜邊OP=r. 根據銳角三角函數的定義，即可以用x，y，r來描述α的正弦值和余弦值：sinα==，cosα==.

設計意圖：教師通過引申鋪墊進行新課導入，在溫故知新中回到新知的源頭，符合學生的認知需求，使得新課的導入水到渠成[2]. 這里的情境引入從學生的現有知識水平和認知能力出發，并及時進行必要的啟發，引領學生進行自主探究和合作交流，實現了學生思維的“再創造”，有利于學生抽象思維的塑造.在整個過程中，以教師的提問為導向，通過觀察、思考、分析、討論，有效鍛煉了學生的數學思維，學生共同體會運用坐標系進行研究的策略，實現認識的飛躍. 此處探究而得到的結論不僅包含了銳角三角函數的定義，同時也滿足了任意角的情形，為后期更加深刻地理解和認識“任意角三角函數”的定義奠定了良好的基礎. 當然，對于以上的課堂導入，倘若教師在細節處多一些雕琢，讓提問更加富有創意，就更容易激起學生的探究興趣，相信也能創造出更多的精彩生成.

以“探究性活動”來培養直觀想象素養

直觀想象素養是一種重要的數學思想和方法，利于學生運用空間想象能力思考問題的習慣的養成，利于學生更好地構建數學體系，利于學生論證數學概念能力的形成. 因此，教師不妨通過開展探究性活動，輔以動機誘導，將想象和探究的主動權交給學生，并對學生的大膽聯想予以充分的肯定，對想象中合理的成分適時給予鼓勵，進一步激發學生自發自覺地運用直覺思維去發現、提出、分析和解決問題，運用已有的知識與經驗，插上“直觀想象”的翅膀，使其放飛思維，自主構建新知.

【教學片段2】

問題1：既然角的概念已經推廣開了，那么任意角的三角函數該如何定義呢？

師生活動：先讓學生去想象和思考，使其得出主觀性判斷，再輔以幾何畫板演示，同時讓學生通過觀察圖形，形成一定的認識.

問題2：大家一起思考，如何能讓探究所得的定義式更加簡潔？

師生活動：呈現問題的同時，以多個問題的鋪開來引導學生進行討論，最終引入單位圓.

問題3：現在該如何完善其定義呢？

師生活動：在學生提煉得出定義之后，教師及時整理和提煉.

問題4：從定義出發，探求任意角α的3個三角函數值的本質是什么.

師生活動：從問題中獲得感悟，同時凸顯三角函數概念的本質.

設計意圖：探究活動是否能取得實實在在的成果已然成為探究性教學的主要追求.上述過程中，教師牢牢把握學生的知識水平，以發展學生的直觀想象素養為核心出發，創設彼此關聯和螺旋上升的“問題串”，激活學生的思維，使其在探究的過程中積極思考、大膽想象，獲得新知，形成感悟. 以上活動是學生自己的活動嗎？學生都經歷了探究和思考的歷程嗎？顯然，在以上探究中，教師給予了學生獨立思考的機會，為學生創造了自主探究和合作交流的過程，使其獲得了一種良好的學習能力，有助于實現自我突破，同時實現直觀想象素養的發展.

以“變式訓練”來培養創新能力

思維的創造性是一種重要的思維形式，將激勵學生思維的發散性、求異性和創造性貫穿于教學活動，不僅是新課程標準的要求，也是孕育核心素養的前提.數學教學中孕育著豐富的創新素材，教師需從數學學科本身的特點和數學規律出發，積極探索訓練學生創新能力的方法. 因此，教師可通過變式訓練來強化對核心概念的系統認識，來培養學生的創新精神.

【教學片段3】

例題：已知角α的終邊經過點P，-，試求出角α的正弦值、余弦值和正切值.

變式1：試求出的正弦值、余弦值和正切值.

變式2：已知角α的終邊經過點P（-3，-4），試求出角α的正弦值、余弦值和正切值.

設計意圖：“一題多變”是溝通學生與素養之間的一座橋梁. 教師從簡單問題入手，運用好變式訓練讓學生從定義出發探究不同情況下的三角函數值，在深化定義理解的同時強化定義應用與幾何的關聯，使學生進入創新思維的佳境.

以“歸納提煉”來培養歸納概括素養

從教學的終極目標來看，教師的教需要以促進學生主動地學來實現核心素養的培育和學生自主發展的目標.教學過程中，教師不可包辦或代替學生的學，教師需要為落實學生數學思維的發展而教. 從而，探究學習的過程應該讓學生來完成，歸納提煉的任務更應該讓學生來完成. 只有這樣，才能獲得具有價值的數學結論，形成清晰而系統的知識體系，培養歸納概括素養.

【教學片段4】

問題1：請試著闡述如何利用單位圓得出任意角三角函數的定義.

問題2：請試著歸納一下在今天的學習中，我們利用定義解決了哪些問題.

設計意圖：從認知的角度來看，學生自己總結和歸納得出的結論才是最富有價值的，也是知識生長的最佳方式. 從而在這個教學環節中，教師不能包辦學生的學習，應該讓學生去總結、歸納和提煉，更好地培養歸納概括素養.

總之，新課程理念下，教師的教需要落實在學生的學之上，需要學生積極主動地去掌握數學基本知識技能，發展數學思維，培養數學核心素養，使得各種關鍵能力得以充分發展[3]. 因此，教師需從傳統教學中的錯誤教學理念中走出來，以學生的需要開展教學活動，積極尋找核心素養的“生長點”，與時俱進地改進數學課堂，讓學生的思維更好地發展，讓數學核心素養落到實處，讓課堂教學更加有效，這樣才能真正符合新課程理念的要求.

參考文獻：

[1] ?黃曉學，李艷利. 論數學教學設計的創意生成點[J]. 數學教育學報，2010，19（06）.

[2] ?柯躍海. 高考數學試題情境的創設實踐[J]. 中國考試，2020（06）.

[3] ?盧娟，孫道斌. 在深度對話中讓數學概念課教學走向本真——“§5.1定義與命題”教學實錄與點評[J]. 中學數學雜志，2017（10）.

2466501186274