從數形結合思想切入初中數學核心素養的培養

歸愛琴

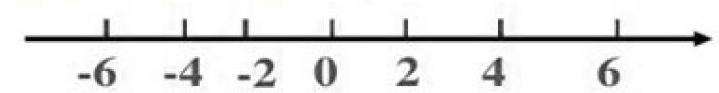
【摘 要】在新課程改革的背景下，初中數學教學過程當中也特別注重學生核心素養的培養，通過培養學生數學核心素養，可以促進學生綜合能力的提升，讓學生在學習的過程當中善于發現問題、分析問題，對問題進行探究，進而解決問題。而在學生數學核心素養培養的過程當中，其數形結合思想的應用是非常重要的，它可以將數與形之間，進行有效的結合和互變，簡化數學問題，從而提高學生學習數學的效率。

【關鍵詞】數形結合思想;初中數學;核心素養;培養

數和形自古以來就是數學當中的兩大主要研究對象，通過數形的有效結合，可以將數量上的關系與相應的幾何圖形進行相關聯，進而探索出問題的答案。在數與形的結合過程當中，可以拓展學生的數學思維，提高學生對數學知識的應用能力，從而促進學生數學學科核心素養的形成。所以在初中數學教學過程當中，老師一定要注重數形結合的思想的應用，引導學生在課堂上對相關問題進行主動探究，培養學生的數學創新能力，提高學生的解題速度，豐富學生的解題思路，從而有效的落實新課程改革當中培養學生學科核心素養的要求。

一、采用數形結合思想對培養初中學生數學核心素養的意義

初中階段的數學課程內容在慢慢的由直觀化向抽象化進行轉變，隨之數學內容的難度也會逐漸增加。這就意味著初中生在學習數學的過程當中，將會面臨更多的挑戰。所以在數學教學過程當中，老師可以將數形進行有效的結合，把抽象的數學問題通過圖形直觀的表示出來，讓學生的思維更加形象化，提高學生對數學知識的理解程度，這對培養學生數學核心素養具有非常積極的意義。在初中數學教學過程當中可以通過以下幾個方面來進行數學思想的應用。其一，可以將相關的數學內容通過代數建模直觀的表現出來，像初中數學里面涉及到的方程、不等式、函數等數學知識，都可以利用相關的代數建模，讓學生對數學知識進行直觀的認知和理解。其二，對于初中數學里面涉及到函數、不等式等知識，可以利用幾何建模直觀的反映問題。其三，老師在教學過程當中可以充分運用數形結合的思想，尤其是在學習函數和幾何知識相關內容的時候，可以通過數學建模，直觀展現教學內容，促進學生對數學知識進行高效理解和吸收，進而讓學生學會運用一定的數形結合思想去解決數學問題，培養學生靈活運用數學知識的能力以及解決實際問題的能力，為學生數學核心素養的形成奠定良好的基礎。

二、在初中數學思想教學過程當中，對數形結合思想的具體應用

（一）在初中數學有理數教學內容當中對數形結合思想的應用

在初中數學教學過程當中，數軸知識的學習為數形結合思想的應用奠定了良好的基礎，也有效的解決了學生對有理數學習的難度。因為每一個有理數都可以在數軸上找出它唯一的對應的那個點，所以對兩個已知有理數進行大小對比的時候，就可以采用數軸的方法，將兩個有理數的具體位置在數軸上標注出來，其大小對比結果一目了然。同時在學習相反數和絕對值相關數學知識的時候也可以利用數軸，以原點為對稱點，然后來描述具體的絕對值和相反數的位置。并且在后期學習實數的過程當中，也可以利用數軸對實數的大小進行直觀比較。所以在數學教學過程當中，老師對這幾個部分教學內容學習的時候，都可以給學生教授相應的數形結合方法，也就是將有理數和數軸進行緊密結合，引導學生通過建立數軸，對有理數、絕對值、相反數以及實數的內容進行一定的了解和運用。

比如在進行“有理數”學習的時候，教學時以生活當中常見的溫度計來提出數軸，它通過數軸將數與形集于一體，以平面圖像的形式，進行負數的學習，例如如下圖所示：+2與-2，+4與-4，+6與-6，它們都是以距離原點0距離相等位置分布在數軸的兩邊，可以更加形象的看出負數的意義，呈現出來的數量關系非常的直觀。

（二）在初中數學方程教學內容當中對數形結合思想的有效應用

方程作為初中數學教學當中的重點內容，它往往是以代數的形式呈現在學生的面前，但是僅僅采用代數的方法來解決方程相關問題，有時候顯得過于繁瑣，加大了解方程的難度，而在解方程的過程當中采用圖形結合的思想，可以將方程演變成函數，然后做出一定的函數圖像，進而簡單直觀的解決相關問題。

例如，已知方程|a2-6a+6|=b方程有4個根，求b的取值范圍。

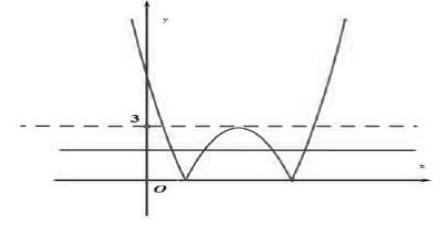
由題目當中可知，已知方程有4個根，那我們在解題的時候可以將其利用圖形結合的思想將其轉化成函數圖像的交點問題。去掉已知方程的絕對值，令y=a2-6a+6得出y=（a-3）2-3將a看成x，坐標軸上畫出函數的圖像，然后將函數y以x軸為對稱軸向上翻折就可以得到已知函數y=

|a2-6a+6|的圖像，然后，我們再令y=b，再做出y=b的函數圖像，這時我們觀察兩個函數圖像，很容易發現函數圖像上兩個圖像的4個交點就是已知方程的4個根，當然b的取值范圍為（0，3）也就顯而易見了，問題就很容易得到解答了。

如果在解決上述問題的時候，不利用圖像進行直觀表示的話，通過一定的運算來得出相應的結果，那是相當復雜而且具有一定難度的。但是如果轉換思路，將題目當中的方程以函數的形式利用相關的圖像表現出來，就可以很容易的得出問題的答案，這不僅大大降低了問題的難度，而且提高了學生的解題效率。

（三）在初中數學教學過程當中，采用數學結合思想培養學生的數學核心素養

通過以上數形結合思想在有理數和函數當中的具體應用，我們就可以看出，通過數形結合的思想可以將數學問題當中比較難以理解和難以計算的參數直觀的表現在圖像上，并且清楚的反映出相關數學參數與圖像之間的關系，進而很快的得出問題的答案。學生在利用相關數學問題與圖像建立關系的過程當中，他們的思維得到了一定的拓展，而且學會了如何將數學抽象的理論知識進行一定的化簡，從而利用簡單的圖像法來探究問題、解決問題，培養學生的探究能力和創新能力。并且利用數形結合的方法解決數學問題讓學生的思維更加活躍，不僅提高了學生的解決問題的效率，而且也讓學生對數學本質的意義進行更深層次的理解，從而促進學生數學核心素養的培養。

比如在學習初中數學勾股定理相關知識的時候，一般老師首先都會引用公式a2+b2=c2，如果采用代數的理念來對勾股定理進行一定的理解，那是具有一定難度的，而且也是沒有辦法推導出a2+b2=c2的。所以這個時候就可以將三角形引入其中，將a，b，c導入圖形當中，并且將三角形放在正方形當中進行不斷的變換，讓學生去觀察變化后圖形的相關規律和特點，進而引導學生對公式進行推導。對于數學當中的相關定理的推導，一般都要借助圖形來進行公式的推導過程，這樣才能夠讓學生更深層次的理解其數學定理的來源，也大大提高了學生對數學定理的應用能力。

三、如何將數形結合思想有效的切入到初中數學核心素養的培養當中

（一）對教學方式進行一定的優化和創新

在初中數學教學過程當中，采用有效的數形結合思想，可以持續性的培養學生的數學核心素養。不過在教學過程當中，老師也要注重教學方法的應用。目前在新課改的背景下，很多老師都摒棄了題海戰術的傳統教學方法，但是題海戰術在一定的教學情況下還是有明顯的效果的，它可以幫助學生提高解題速度。目前老師在對學生進行相關習題訓練的時候，可以將科學的數形結合思想與傳統的教學方式進行有效的融合，從而提升學生在數學方面的綜合能力。

比如在學習圓的相關知識的時候，因為這個章節里面涉及的內容比較多，所以老師為了提高教學效率，一般都會采用數形結合的方式來將圓與直線的關系進行一定的展示，讓學生更加透徹的明白，圓與直線的相交、相離、相切這三種關系，這樣不僅加深了學生對有關于“圓”知識概念的理解，而且也為后面有關于圓的計算奠定了良好的基礎。

（二）在數學教學過程當中要不斷拓展學生的思維

學生在初中數學教學過程當中，對數學知識的不斷積累，也代表著學生解決數學問題的能力也在不斷的進行提升，當然數形結合思想在學生數學能力提升的過程當中發揮著至關重要的作用。所以在數學教學過程當中，老師要不斷的強化學生的數形結合能力。在課堂上以學生為主體，跟學生進行積極主動的互動交流，引導學生對數學當中存在的問題進行分析和研究，并且在關鍵時候給予有效的指導，引導學生利用數形結合的方法尋找解題的思路和出口，從而改變學生在解決數學問題當中的定向思維，讓他們的思維得到一定的拓展，進而提高學生解決問題的能力。

比如在學習“數據的收集，整理與描述”的相關數學知識的時候，它需要學生對相關事件進行普查和抽樣調查，但是里面涉及的相關數據比較繁雜，單單靠代數知識是沒有辦法進行直觀展示的，所以這個時候就可以利用統計圖和統計表來將相關數據進行有效的整理，根據統計圖和統計表里面反映的情況，進行相應的代數計算，這樣就可以大大簡化了代數方面的繁瑣數據，直觀的將調查結果展示出來，不僅讓學生掌握了統計學方面的知識，也讓學生學會了利用數學知識解決生活實際問題。這對培養學生數學核心素養具有非常大的促進作用。

四、結束語

總而言之，數形結合思想作為初中數學教學過程當中的主要思想，它能夠幫助學生理解數學當中很多比較抽象的概念，簡化數學當中比較復雜的題目，豐富學生的解題思路，提高學生的解題效率。所以在教學過程當中，老師一定要注重學生數形結合的思想的運用，在課堂上利用直觀的圖形將數學的實質展示出來，讓學生對相關數學概念進行深層次理解和掌握，從而培養學生的學習興趣，并且在課堂上不斷的引導學生進行實踐操作，學會利用代數知識解決圖形問題，利用相關圖形解決代數問題，并且將代數知識與圖形進行有效結合解決數學問題，拓展學生的解題思路，促進學生發散思維能力的提升，從而幫助學生培養良好的數學核心素養。

【參考文獻】

[1]馬雙平.數形結合在初中數學教學中的運用分析[J].科技資訊，2020，18（11）：155-156.

[2]余云洲.相互滲透，交叉作用——初中數學教學中數形結合思想的應用探析[J].教育現代化，2019，6（06）：114-

115+170.

[3]許婷婷.行走在數學核心素養下數形結合理念的創新之路——以《加法交換律和結合律》為依托的教學課例研究[J].華夏教師，2018（21）：29-30.