核心素養(yǎng)下高三數(shù)學(xué)復(fù)習(xí)課教學(xué)研究

朱小東

[摘? 要] 數(shù)學(xué)學(xué)科是最重要的基礎(chǔ)學(xué)科之一，它的六大核心素養(yǎng)不僅是學(xué)生學(xué)習(xí)數(shù)學(xué)的重要目標(biāo)——促進(jìn)學(xué)生終身思維發(fā)展;也是學(xué)生學(xué)習(xí)數(shù)學(xué)綜合能力的體現(xiàn)——利用數(shù)學(xué)思維解決實(shí)際問題. 而高三數(shù)學(xué)復(fù)習(xí)課正是培養(yǎng)和彌補(bǔ)學(xué)生數(shù)學(xué)核心素養(yǎng)的重要機(jī)會(huì). 文章通過研究目前高三數(shù)學(xué)復(fù)習(xí)課存在的問題，提出相應(yīng)的解決方法和對(duì)策，以此提高數(shù)學(xué)復(fù)習(xí)課的效率和質(zhì)量.

[關(guān)鍵詞] 高三數(shù)學(xué);復(fù)習(xí)課;核心素養(yǎng);效率

復(fù)習(xí)課的重要性眾所周知，說遠(yuǎn)一點(diǎn)，它對(duì)學(xué)生系統(tǒng)掌握知識(shí)，發(fā)展思維能力具有重要作用;說近一點(diǎn)，它對(duì)學(xué)生高考成績的影響力不言而喻. 復(fù)習(xí)課是教師培養(yǎng)學(xué)生數(shù)學(xué)核心素養(yǎng)，也是教師教學(xué)補(bǔ)缺、提高教學(xué)質(zhì)量不可缺少的環(huán)節(jié). 上好一堂復(fù)習(xí)課并不是一件輕而易舉的事，如果不認(rèn)真安排，不精心設(shè)計(jì)，不僅達(dá)不到預(yù)期的效果，還會(huì)產(chǎn)生多種問題.

■目前高三數(shù)學(xué)復(fù)習(xí)課存在的問題

當(dāng)下，提及高三數(shù)學(xué)復(fù)習(xí)課，教師總會(huì)將其與“重復(fù)舊課”“真題練習(xí)”“題海練習(xí)”“重難點(diǎn)聚集”等聯(lián)系在一起，這些都是教師高考“押寶”的重要環(huán)節(jié)，而對(duì)于學(xué)生數(shù)學(xué)抽象、邏輯推理、數(shù)學(xué)建模、直觀想象、數(shù)學(xué)運(yùn)算、數(shù)據(jù)分析的培養(yǎng)猶如蜻蜓點(diǎn)水，一帶而過. 下面，筆者將結(jié)合具體案例，剖析高三數(shù)學(xué)復(fù)習(xí)課目前存在的一些主要問題.

1. 重復(fù)舊課

近年來，高考主要考查學(xué)生的“雙基”——基礎(chǔ)知識(shí)、基本技能，這成了許多教師高三復(fù)習(xí)數(shù)學(xué)的主要目標(biāo)，這本是正確的指向，但是許多教師對(duì)基礎(chǔ)知識(shí)、基本技能的理解走上了錯(cuò)誤的渠道. “重復(fù)舊課”似乎又讓學(xué)生回到了高一、高二的新課教學(xué)，將大部分的基礎(chǔ)知識(shí)重新拉上了復(fù)習(xí)課堂. 這不僅浪費(fèi)了復(fù)習(xí)時(shí)間，而且會(huì)讓學(xué)生感到枯燥乏味. 復(fù)習(xí)課是鞏固基礎(chǔ)知識(shí)，提高基本技能的課堂，而非新課教學(xué)的初次介入. 例如，三角函數(shù)的基本性質(zhì)一直以來都是高考重點(diǎn)考查的知識(shí)點(diǎn)，特別是圖像、定義域、值域、單調(diào)性、周期性等，由于這些都是三角函數(shù)的重要性質(zhì)，因此復(fù)習(xí)時(shí)教師容易抓住這些知識(shí)點(diǎn)不放，不斷地針對(duì)單獨(dú)性質(zhì)做習(xí)題練習(xí). 這種復(fù)習(xí)方法表面看來似乎抓住了重點(diǎn)，其實(shí)是忽略了三角函數(shù)的基本性質(zhì)在高考中主要是作為解決其他問題的基本工具，如幾何、代數(shù)等. 由于教師在復(fù)習(xí)課堂上忽略了這種思想的引入，將鞏固基礎(chǔ)知識(shí)和提高基本技能的復(fù)習(xí)課又上成了舊課.

2. 層次不分

高中數(shù)學(xué)的分層次教學(xué)已有不少文章討論過，例如，文[1]就探討了“為什么要實(shí)行高中數(shù)學(xué)分層次教學(xué)”“高中數(shù)學(xué)分層次教學(xué)意思何在”“怎樣實(shí)行高中數(shù)學(xué)分層次教學(xué)”等，關(guān)于這些方面的具體討論，本文不再贅述. 不少教師都能注意到分層次教學(xué)對(duì)學(xué)生個(gè)體發(fā)展的各種優(yōu)勢，不僅能因材施教讓教學(xué)面向全體學(xué)生，還能提高學(xué)生的學(xué)習(xí)興趣和學(xué)習(xí)水平. 但由于高三的時(shí)間緊、任務(wù)重，而且面臨的是緊張又重大的高考，因此教師在復(fù)習(xí)課之中就有意或無意地將分層次教學(xué)拋向了腦后. 不顧學(xué)生基礎(chǔ)知識(shí)的掌握情況，不顧學(xué)生基本技能的差異，用“一刀切”的方式將復(fù)習(xí)課程帶上了課堂. 不僅如此，層次不分還涵蓋在教師對(duì)復(fù)習(xí)知識(shí)的分類整理，對(duì)重難點(diǎn)的分析以及思想和方法的指導(dǎo)上，容易形成重實(shí)踐、輕理論的問題. 例如，在立體幾何的復(fù)習(xí)課，教師重視的是公式的實(shí)踐使用，而忽視了對(duì)學(xué)生在空間感、轉(zhuǎn)化思想、幾何直觀及運(yùn)算能力上的培養(yǎng)和彌補(bǔ)，因此造成了學(xué)生上行下效、無法自主思考的場景.

3. 順次復(fù)習(xí)

許多教師都明白，復(fù)習(xí)課不是一蹴而就的，需要循序漸進(jìn)地歸納、總結(jié)基礎(chǔ)知識(shí)和重要的知識(shí)點(diǎn)，需要循序漸進(jìn)地指導(dǎo)學(xué)生完整掌握系統(tǒng)知識(shí)，但同樣容易對(duì)循序漸進(jìn)的理解產(chǎn)生偏差，而忽視了復(fù)習(xí)知識(shí)的前后進(jìn)度、系統(tǒng)分類，最終形成了“順次復(fù)習(xí)”. 如何將“循序漸進(jìn)”和“順次”區(qū)分開來，是教師上好復(fù)習(xí)課的難點(diǎn)之一，首先就得理解其中的含義：“循序漸進(jìn)”說的是復(fù)習(xí)時(shí)間和空間的順序，而“順次”說的是課本內(nèi)容按部就班講解的前后順序. 例如，一些教師在復(fù)習(xí)“圓錐曲線”時(shí)，容易順次地分開橢圓、雙曲線、拋物線以及圓的定義和性質(zhì)進(jìn)行復(fù)習(xí)講解，特別是對(duì)方程、公式的運(yùn)用，也許還能夠做到與函數(shù)、不等式、方程、三角、向量等相關(guān)知識(shí)的綜合復(fù)習(xí)，但卻容易忽視圓錐曲線的內(nèi)在聯(lián)系——如橢圓與圓內(nèi)在聯(lián)系的深度挖掘?qū)鉀Q橢圓問題的優(yōu)勢[2]，以及缺乏對(duì)幾何抽象、數(shù)學(xué)建模的培養(yǎng)和彌補(bǔ)，而且對(duì)學(xué)生在復(fù)習(xí)期間關(guān)于幾何的數(shù)學(xué)表達(dá)也毫不在意.

■高三數(shù)學(xué)復(fù)習(xí)課問題的應(yīng)對(duì)之策

每位教師在高三數(shù)學(xué)復(fù)習(xí)之中存在的問題各有不同，筆者針對(duì)主要問題，按照自身的教學(xué)經(jīng)驗(yàn)，對(duì)解決高三數(shù)學(xué)復(fù)習(xí)課問題提出了以下建議，供同行參考.

1. 統(tǒng)計(jì)記錄，資源共享

在高三復(fù)習(xí)期間，時(shí)間對(duì)教師和學(xué)生是緊密的，因此教師在平時(shí)教學(xué)中，就要開啟記錄統(tǒng)計(jì)，充分重視資源的整合和共享，加強(qiáng)同行之間的聯(lián)系和合作.

第一，在平時(shí)教學(xué)之中，教師要善于記錄學(xué)生在學(xué)習(xí)時(shí)存在的困難，包含學(xué)生對(duì)知識(shí)的理解和心理情況;制作統(tǒng)計(jì)單，包含知識(shí)難點(diǎn)、知識(shí)重點(diǎn)、思想和方法、心聲表達(dá)等，指導(dǎo)學(xué)生完成統(tǒng)計(jì)記錄，有利于后期的資源整合、分析和分享，避免時(shí)間浪費(fèi).

第二，加強(qiáng)同行交流，特別是與外地同年級(jí)教師的交流. 交流教學(xué)方法和教學(xué)心得，共享教學(xué)資源，觀察、實(shí)驗(yàn)、歸納、類比等思想和方法并非教育學(xué)生所有，教師的自我發(fā)展同樣缺一不可.

2. 層次分明，提高學(xué)生的積極性

層次分明不僅要注意學(xué)生個(gè)體基礎(chǔ)知識(shí)和基礎(chǔ)能力的差異性，還要留意對(duì)知識(shí)的分類整理，理清復(fù)習(xí)目標(biāo)，達(dá)到復(fù)習(xí)的針對(duì)性.

第一，高三數(shù)學(xué)復(fù)習(xí)一般分為第一輪復(fù)習(xí)、第二輪復(fù)習(xí)和第三輪復(fù)習(xí). 針對(duì)每一輪復(fù)習(xí)，教師首先要理清各輪復(fù)習(xí)的目標(biāo)和要求：第一輪復(fù)習(xí)的目標(biāo)和要求是提高學(xué)生對(duì)基礎(chǔ)知識(shí)的記憶、理解和熟練度，引導(dǎo)學(xué)生加強(qiáng)自主復(fù)習(xí)，將學(xué)生自主復(fù)習(xí)存在的難點(diǎn)表現(xiàn)出來，提高學(xué)生復(fù)習(xí)過程中補(bǔ)缺知識(shí)的意識(shí). 第二輪復(fù)習(xí)的目標(biāo)和要求是整合知識(shí)，構(gòu)建知識(shí)體系. 知識(shí)體系主要分單元知識(shí)體系（以單元為主整合的教材內(nèi)容）和知識(shí)點(diǎn)體系（以知識(shí)點(diǎn)的內(nèi)在聯(lián)系為主整合的教材內(nèi)容），教師要引導(dǎo)學(xué)生從構(gòu)建知識(shí)點(diǎn)體系出發(fā)，逐漸整合成單元知識(shí)體系，加強(qiáng)學(xué)生多元、多角度、多層面地了解知識(shí)，正確靈活地遷移知識(shí). 第三輪復(fù)習(xí)的目標(biāo)和要求是增加習(xí)題練習(xí)量和針對(duì)性，提高學(xué)生對(duì)知識(shí)的運(yùn)用程度，加強(qiáng)學(xué)生綜合解題能力，但這并非融入題海，一是題目的選擇要有針對(duì)性和層次性，二是題目的選擇要有方法歸納、知識(shí)內(nèi)聯(lián)和思想滲透.

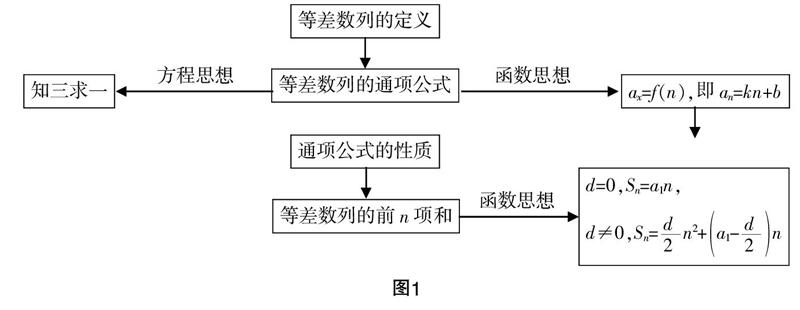
第二，知識(shí)分類整理. 知識(shí)的分類整理不僅涉及知識(shí)體系的建構(gòu)，而且影響數(shù)學(xué)思想和方法的整理與掌握. 那么對(duì)知識(shí)的分類整理主要包含幾個(gè)要點(diǎn)：（1）先按知識(shí)點(diǎn)引導(dǎo)學(xué)生將基礎(chǔ)知識(shí)——概念、定義、定理等整理成思維導(dǎo)圖（例如等差數(shù)列的導(dǎo)圖，如圖1），理清它們的區(qū)別、聯(lián)系，區(qū)分重點(diǎn)、難點(diǎn). （2）按照知識(shí)點(diǎn)編制一些有針對(duì)性的，由單項(xiàng)（單獨(dú)知識(shí)點(diǎn)）到綜合（知識(shí)點(diǎn)相連），由基本到變式，難度逐漸增大、層次不一的練習(xí)題，讓學(xué)生邊復(fù)習(xí)邊練習(xí). （3）對(duì)學(xué)生知識(shí)掌握情況的分類整理，例如，教師在學(xué)生做完練習(xí)題之后，分析卷面情況，統(tǒng)計(jì)具有普遍性的易錯(cuò)題、重點(diǎn)題、難點(diǎn)題;課程學(xué)習(xí)完成之后，統(tǒng)計(jì)學(xué)生在復(fù)習(xí)期間的學(xué)習(xí)進(jìn)步情況、知識(shí)突破障礙等.

3. 遵循復(fù)習(xí)原則

復(fù)習(xí)是一個(gè)系統(tǒng)過程，其猶如建筑工程一樣，遵循相應(yīng)的原則，既能保證復(fù)習(xí)過程順利完成，又能減少復(fù)習(xí)困難，實(shí)現(xiàn)事半功倍的效果.

（1）自主性原則. 在復(fù)習(xí)過程中，要以學(xué)生為主，充分發(fā)揮學(xué)生的自主性，讓學(xué)生積極、主動(dòng)地參與復(fù)習(xí)全過程. 復(fù)習(xí)過程是一個(gè)復(fù)雜的系統(tǒng)過程，但綜合其本質(zhì)，可以概括為學(xué)生與知識(shí)之間的交流過程. 在這個(gè)過程中，學(xué)生才是主體，教師主要是學(xué)生與知識(shí)的溝通橋梁. 只有把學(xué)習(xí)的主動(dòng)權(quán)交還給學(xué)生，才能充分調(diào)動(dòng)學(xué)生學(xué)習(xí)的積極性和主動(dòng)性，激發(fā)學(xué)生的學(xué)習(xí)興趣，真正作為學(xué)習(xí)的主人.

（2）針對(duì)性原則. 由于復(fù)習(xí)過程面臨的知識(shí)點(diǎn)多，覆蓋面廣，容易造成復(fù)習(xí)指向混亂，知識(shí)遷移找不到目標(biāo)，所以在復(fù)習(xí)過程中，除了要牢固掌握基礎(chǔ)知識(shí)之外，必須突出重點(diǎn)、難點(diǎn)、疑點(diǎn)、易錯(cuò)點(diǎn)、易混點(diǎn)等，緊扣各點(diǎn)設(shè)計(jì)復(fù)習(xí)內(nèi)容，做到因材施教、有的放矢.

（3）系統(tǒng)性原則. 復(fù)習(xí)過程其實(shí)也是一個(gè)“點(diǎn)—線—面”的知識(shí)總結(jié)過程，在這個(gè)過程中，通過知識(shí)點(diǎn)的縱橫聯(lián)系可以幫助學(xué)生構(gòu)建知識(shí)網(wǎng)絡(luò)，使得學(xué)生分散的知識(shí)系統(tǒng)化. 而且，復(fù)習(xí)過程包含了記憶、整理、分析、練習(xí)、評(píng)價(jià)等具體步驟，每個(gè)步驟都是不可缺少的環(huán)節(jié)，當(dāng)各個(gè)步驟能做到環(huán)環(huán)相扣的實(shí)效時(shí)，復(fù)習(xí)程序才真正具有系統(tǒng)性.

總之，復(fù)習(xí)不是簡單的重復(fù)，它的最終目的是幫助學(xué)生在繁多的知識(shí)中梳理知識(shí)脈絡(luò)、建立知識(shí)結(jié)構(gòu)，培養(yǎng)學(xué)生的數(shù)學(xué)核心素養(yǎng)，為學(xué)生運(yùn)用數(shù)學(xué)知識(shí)和數(shù)學(xué)思維解決實(shí)際問題鋪好道路.

參考文獻(xiàn)：

[1]? 康天福. 高中數(shù)學(xué)分層次教學(xué)探討[J]. 課程教育研究，2016（08）.

[2]? 揭麗群，劉詠梅. 化歸思想下的解題教學(xué)——以一道圓錐曲線試題為例[J].中學(xué)數(shù)學(xué)研究，2014（02）.