新課標引導下“指數函數（第一課時）”教學再設計

肖輝

[摘? 要] 《普通高中數學課程標準（2017年版）》的實施是深化普通高中課程改革的重要環節，更加突出以學生發展為本，把立德樹人作為教育的根本任務，著重提出培養和提高學生的數學核心素養. 課程結構發生了很大的變化，更加關注數學邏輯體系、內容主線、知識之間的聯系，重視數學實踐和數學文化，課程內容以主題式展開替代過去的模塊組合. 核心素養并不是與生俱來的，而是通過后天教育習得的. 只注重知識點的課時教學設計，學科視角就容易受限，不利于培養學生從全局看問題和解決問題的能力，從而難以聚焦學生核心素養的形成. 單元教學可以站在“學生為本”的角度，以學科具體核心素養為綱領，整合優化課程結構，突出主線，避免狹隘的課時視角，以“大觀念”的視野讓學生的學科核心素養得到提升.

[關鍵詞] 高中數學;單元教學設計;指數函數

章建躍博士在2012年《中小學數學（高中版）》的“編后漫筆”中提出：“注重整體性才是好數學教學.”具體來說，就是“教學中應注意溝通各部分內容之間的聯系，通過類比、聯想、知識的遷移和應用等方式，使學生體會知識之間的有機聯系，感受數學的整體性，進一步理解數學的本質，提高解決問題的能力”.

單元教學設計是在整體把握教材的基礎上，用全局的眼光、系統的方法把教材中具有內在聯系的知識進行整合、重組并形成相對完整、動態的教學設計. 主張學生的學習內容與學習活動應該是一個整體，從目前高中數學教學的實際情況來看，大多數教師還是把精力放在具體某節課上，只注重細節的處理，而忽視了教材的整體性與系統性. 這種“只見樹木不見森林”的課堂教學設計會導致學生的知識碎片化，難以形成一個完整的知識體系，進而導致部分學生知識遺忘率偏高、基礎不扎實等問題. 而單元教學設計正是在新課標的背景下，依據學生的認知特點，整體把握教材，對教材中具有內在聯系的知識進行整合、重組并直指學生核心素養的教學設計.

那么，如何實施單元教學設計？筆者以“指數函數（第一課時）”為例，嘗試實施單元教學設計.

在“指數函數”的教學過程中，筆者用五個大問題串聯起了整節課的教學內容：

問題1：請拿出一張白紙（面積記為單位1），分別記錄這張白紙經過一次、兩次、三次對折后的層數與面積. 經過x次對折后，其層數y、面積S分別與x有怎樣的關系？這兩個關系中，變量之間能構成函數關系嗎？為什么？

問題2：以上兩個關系式里有何異同點？如何定義指數函數？有沒有類似的經歷或經驗？

問題3：對于一個新的函數，我們可以研究哪些內容？

問題4：該如何研究呢？有沒有成功的經歷或經驗？

問題5：通過今天的學習，我們如何研究一個新函數？請說說你的研究思路.

設計意圖分析：

問題1直指指數函數的定義，雖然是一個特殊的問題，但是將為后面特殊問題一般化做出鋪墊. 新課標強調要循序漸進地加強學生對函數概念的理解，因前面學生剛剛學完函數概念不久，部分學生不一定能完全消化，此處鞏固認知，為后續探究順利做鋪墊.

問題2通過尋找關系式中的異同點，歸納概括關系式中的本質特征. 類比一次函數用y=kx+b（k≠0）的形式表示，反比例函數用y=■（k≠0）的形式表示，二次函數用y=ax2+bx+c（a≠0）的形式表示，且對其一般形式上的系數都有相應的限制，讓學生嘗試從以往的學習經歷中尋找解決新問題的方法，建立探索未知向已知轉化的意識.

問題3的設計，讓學生回顧研究函數問題的一般指向——圖像和性質（值域、單調性、奇偶性、對稱性等）. 這個問題，明確了研究方向.

問題4是本節課教學的難點，是學生思維的制高點. 讓學生思考、明確研究函數的思路和方法是重要的，它屬于觀念、意識層面. 教師通過“如何研究”這一問題的提出，引導學生提煉出如何研究一個新函數的一般思路：

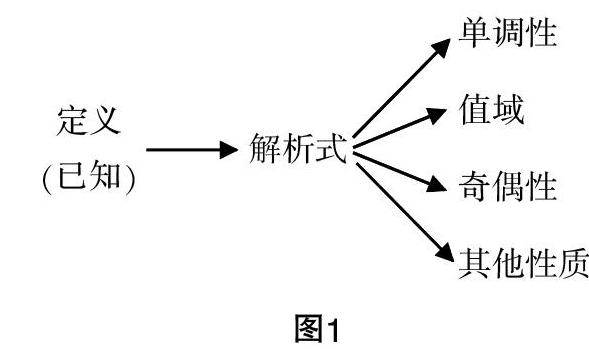
（1）利用指數函數的定義及其解析式研究函數的性質——從數的角度.

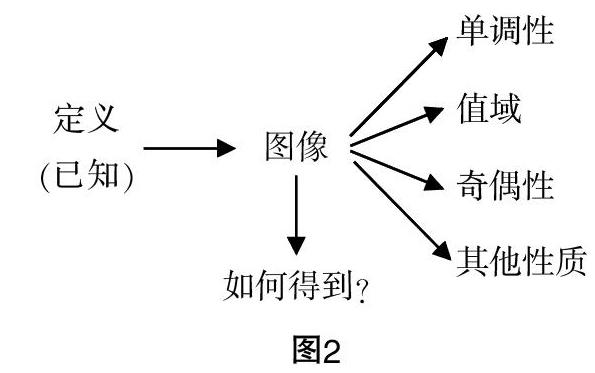
（2）利用函數的圖像來研究函數的性質——從形的角度.

筆者對問題4還設計了以下追問：

追問1：有沒有成功的經歷或經驗？啟發學生回憶具體函數（一次函數、二次函數等）的研究方法與研究結論，以及一般函數的研究方法和路徑，學生較順利地提出了兩種研究思路：（1）利用指數函數的定義及其解析式研究函數的性質——從數的角度;（2）利用函數的圖像來研究函數的性質——從形的角度.

追問2：根據指數函數y=ax（a>0，且a≠1）的解析式，你能得出它的哪些性質？會不會還有其他性質呢？根據解析式能發現它的部分性質，但“數缺形時少直觀”，要研究它的更多性質需要借助函數的圖像，那么如何獲取指數函數的圖像？

函數的學習不是孤立的，而是要站在知識系統整體的高度設計之上. 根據解析式理性分析，再通過圖像直觀感受. 研究指數函數的圖像是本節課的一個重點，描點法作圖是學生必會的基本功，通過讓學生動手畫圖，加深學生對指數函數圖像的認識.當然，讓學生作圖不是為了作圖而作圖，而是為了總結得出畫指數函數圖像的基本方法——描點法和三點作圖法，為以后比較快捷地畫出指數函數圖像奠定基礎;指數函數圖像的學習本著類比、由一般到特殊和由特殊到一般的思想，充分利用幾何畫板進行展示，不斷讓學生做和說，讓學生思考指數函數圖像的變化規律，觀察圖像的共同特征，這樣由前面對指數函數圖像的深度剖析，得出指數函數的性質可謂是水到渠成的事情.

問題5是開放型問題，總結并回顧本節課內容，從知識和方法的角度都有不同的收獲和體會. 怎樣研究新對象、解決新問題更是需要不斷地嘗試與總結.

通過五個大問題的提出，引導學生發現問題→提出問題→尋找解決問題的思路（特殊）→得到解決問題的一般方法（一般）→將其推廣至解決更多問題（特殊）. 通過學生的自主探究活動，使學生掌握了指數函數的圖像與性質，這是本節課的一條明線;同時，在探索對數函數圖像與性質的過程中，讓學生建構研究新函數的一般方法，也完成了本節課的一條暗線的鋪排. 整個教學過程以具體問題來驅動學生進行思考的系統化方式很好地營造了課堂對數學問題的分析和討論的氛圍，調動了學生學習的積極性. 更為重要的是，學生數學分析能力的養成和數學思維的訓練，正是在一個個數學問題的解決中完成的，通過數學建模使得學生從感性認識逐步向數學理性思維發展，豐富了學生的認知體驗過程.

“指數函數”這節課站在單元整體教學的高度，無論從本節課的教學目標還是重難點的把握，我們都可以看出，本節課的教學有兩條線索：一條是明線，即對于指數函數圖像與性質的理解與把握;另一條是暗線，即怎樣研究一類未知的函數，對其基本思路和方法的探究，這也是今后研究和學習的一條主線. 從表面上看，我們的教學是按照明線的目標步步深入的，但從本質上看，對于暗線的探究更為重要，一方面它不但推動了明線的發生和發展，另一方面著眼于將研究函數的方法內化為學生的一種能力，在探究過程中鍛煉思維，為整個單元的教學建立了研究問題的范式. 單元教學設計回歸了學生本位，賦予學生選擇和主動學習的機會和能力，鍛煉了學生的獨立學習能力. 從數學的基礎知識、基本思想、基本方法、基本活動經驗等方面，讓學生對數學有了一個整體的認知結構，提高了學生的數學學習能力和理性精神.