對小學數學“數形結合”的內涵及實踐研究

張春麗

摘 要：在大部分小學生的認知當中，數學概念都是十分抽象且模糊的，為數學教學工作的有效開展帶來了極大阻礙，所以選擇合理的教學方式是提高教學質量的關鍵。文章著眼于小學數學教學中的“數形結合”模式，對這種數學思維方式的內涵、特點和應用價值進行了分析，并論述了“數形結合”思想在小學數學教學中的實踐路徑，希望能為相關工作人員帶來參考。

關鍵詞：小學數學;數形結合;思維模式;教學實踐

一、 引言

直觀化、具體化和形象化的教學方式十分適用于開展小學數學教學，它們可以將抽象的數學概念變得生動形象，進而降低小學生的理解難度并提高他們的學習興趣。為了進一步發揮“數形結合”思維的價值，使其能在小學數學教學中得到更合理應用，相關工作人員應該明確“數形結合”的內涵，并且對其實踐應用情況加以把控。

二、 “數形結合”思維模式的內涵

數字與圖形是數學領域中最為基本的研究對象，雖然它們的表達形式相異，但是基于特定條件，數字和圖形可以相互轉換。這種數字與圖形間的聯系，就是數形結合的基礎。所謂“數形結合”思想模式就是以直觀化的幾何圖形或位置關系，來表達抽象化的數字語言和數量關系。基于此，能實現抽象思維與形象思維的有機結合，將實現抽象問題具體化和復雜問題簡單化，能有效降低數學研究的難度。

現階段，“數形結合”被廣泛應用在數學教學當中，可大大提高函數、集合、方程與不等式、解析幾何內容的教學成效。數與形相結合的思維方式與小學生的階段性思維發展特點十分相符，基于這種方法開展教學更符合以學生為本的素質教育要求，也能有效地引導學生理解知識內涵、完成知識遷移和內化。在滲透和應用“數形結合”時，教師應該遵循等價性、雙向性和簡潔性原則，保證“數形結合”思維模式應用合理，教學成效顯著。當然，在教學環節，教師也必須根據學生的實際學習能力來確定“數形結合”的應用模式，且在教學環節還應該積極構建生活化教學情境，為學生提供快速實現數、形轉換的機會，讓數形結合思維的教學價值得以充分發揮。

三、 小學數學“數形結合”的應用價值

從小學課本內容中，我們不難發現“數形結合”的身影，可見這種思想已經成了小學數學教學的核心思維方式。對于小學數學教師而言，教學工作的開展不僅要培養學生的數形結合思維，為他們開展更為深入的數學研究打好基礎;更要在教學過程中合理應用數形結合思維，為有效傳授知識、達成教學目標做出保障。在實際作業環節，小學數學“數形結合”的應用價值主要體現在如下方面。

（一）激發學生學習興趣

在小學數學課堂上應用數形結合思想，可以大大提升小學生的學習興趣。在教學過程中，教師可引導學生們自主完成抽象概念與圖形的轉化，更讓教學變得更為生動靈活，為小學生創造輕松愉悅的學習環境。同時，教師可以利用多媒體設備展現抽象與想象思維的轉換過程，以更為具象化的形式激發學生的學習積極性。

（二）加強數學知識理解

數形結合思維的應用，可以將抽象的數學概念和定義生動形象地展現出來，這種知識表現形式與小學生的形象思維更為相符，將有效提升他們的理解能力和記憶速度。同時，數形結合思維的應用，可以在一定程度上彌補小學生的個體差異性，可為學生提供更為豐富的解題思路和學習思維，十分有利于提高教學質量。

（三）提升數學解題能力

提高小學生的數學知識應用能力，增強他們的解題技巧是小學數學教學的目標。而應用數形結合思維，將有效提升小學生的數、形轉換能力和理解能力，能讓他們找到最符合自身思維方式和實踐能力的解題方式，將有效提升小學生的數學解題能力。

四、 “數形結合”思維的實際應用路徑

“數形結合”思維的應用，十分有助于提升小學生的學習質量和效率，這種思維模式在教學環節的應用，應該貫穿教學活動始終。在實際作業環節，小學數學教師應該合理應用數形結合教學方法，引導學生們在數學元素相互轉化的過程中完成知識積累和遷移，使他們在輕松愉悅的氛圍之下提高學習高效性。

（一）以形助教

數形結合的最主要應用方式，就是利用直觀化圖形表達抽象的數學概念，為降低數學知識理解難度、提高知識學習速度提供輔助。因此，以形助教就是小學數學教學環節“數形結合”思維的主要應用路徑之一。在教學中，教師必須引導學生利用圖形來“翻譯”知識，實現抽象思維和形象思維的轉換。根據我國義務教育規定，培養小學生的空間觀念也是數學教學的主要目標之一，而在此類型幾何知識教學中應用“數形結合”思維，必然能進一步提升理論與實際的聯系，讓學生能有效連接空間表象和空間想象，進而達到事半功倍的效果。小學數學教師應該在教學環節積極引入基本圖形和實物，積累圖形表述素材，從而保障數、形轉換的有效性;能有效利用線段圖或面積模型，幫助學生快速理解抽象化、復雜化問題，使他們能找到解決要點。

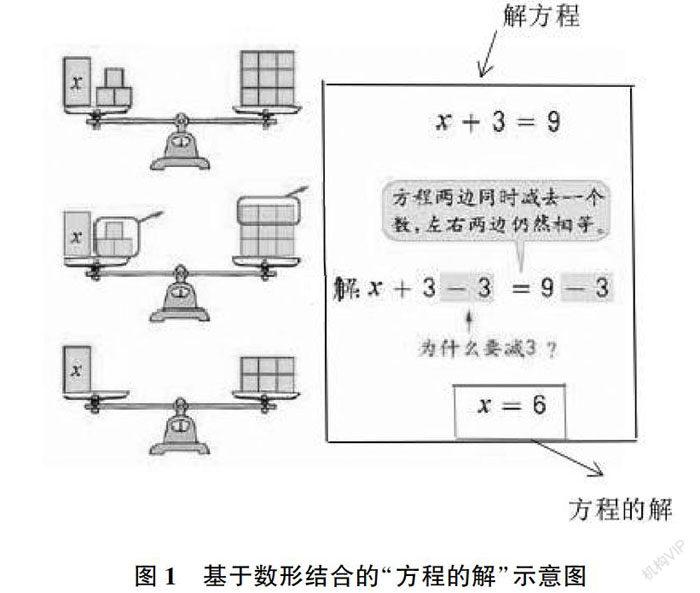
以《體積和體積單位》一課為例，小學教師應該利用課件或實物，引導學生將數學概念或符號與實物相連，進而幫助他們快速地掌握相關知識。比如，學習cm3、dm3、m3等體積單位時，教師可使用橡皮泥或硬紙板來制作相應單位大小的教具，將數學基礎知識轉化為清晰的表象，為他們深入了解和記憶這些知識做好準備。在此環節，教師應該為學生創造合理的教學情境，進而引導他們將數學知識與實踐生活相連，讓他們能深入思考和感受數學的實用價值，進而為有效學習奠定基礎。同時，教師還應該將利用實物或圖像來表示未知數概念，為學生快速掌握方程式的解算原理奠定基礎。比如，在求解方程式x+3=9時，為便于學生理解x的概念和求解方程式，教師可利用天平來解釋等式概念。此時，教師可利用圖1來表示“方程的解”的概念，讓學生從天平必須兩邊重量相等才平衡的特點中明晰等式也必須兩邊平衡這一解題要點，然后引導學生通過簡單的數學加減法求解x。

圖1 基于數形結合的“方程的解”示意圖