淺談數(shù)學核心素養(yǎng)在課堂教學中的落實的策略

郭麗平

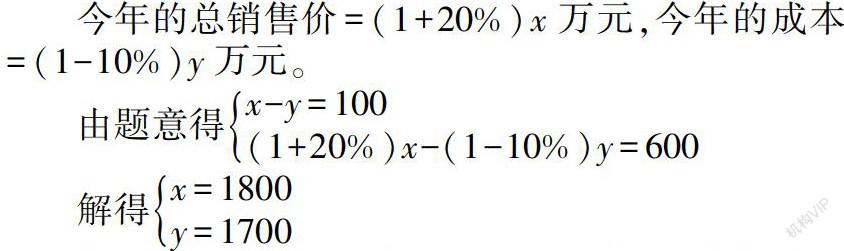
摘 要：數(shù)學核心素養(yǎng)是每個學生學習數(shù)學應該具備的素養(yǎng)，同時數(shù)學核心素養(yǎng)是教育最終的目標。所謂數(shù)學核心素養(yǎng)是學生在學習數(shù)學基礎知識、基本技能的基礎上通過有意識地培養(yǎng)而發(fā)展，但它不同于基礎知識和技能，它是蘊含在基礎知識、基本技能中。

關鍵詞：數(shù)學核心素養(yǎng);課堂教學;基礎知識

一、 數(shù)學核心素養(yǎng)的內(nèi)涵

“數(shù)學核心素養(yǎng)”成為最近熱門詞，特別最近幾年中高考不僅考查學生基礎知識和基本技能，越來越重視考查學生數(shù)學核心素養(yǎng)。什么是初中數(shù)學核心素養(yǎng)？

數(shù)學核心素養(yǎng)主要有以下幾個方面：數(shù)學運算、邏輯推理、數(shù)學建模、數(shù)學抽象、直觀想象、數(shù)據(jù)分析。

二、 數(shù)學核心素養(yǎng)在課堂中落實策略

（一）在習題訓練中，發(fā)展學生數(shù)學運算的素養(yǎng)

初中數(shù)學的運算包括數(shù)的運算、式的恒等變形、方程和不等式的變形等。為了發(fā)展學生數(shù)學運算素養(yǎng)，在課堂教學中可以采用以下的策略：

（1）在課堂教學中要重視基礎知識和基本技能的訓練，提高學生的運算能力。在進行數(shù)學運算時，要時時問學生算理依據(jù)是什么，讓學生領悟到基礎知識的重要性，而扎實基礎是數(shù)學運算正確的關鍵。如果基礎知識不扎實，基本技能不過關，往往會導致運算錯誤。

（2）讓學生掌握運算的通法通則。

例1 計算題并寫出依據(jù)

總之在計算過程中，讓學生明白計算的依據(jù)算理，不僅讓學生知其然，然后知其所以然，有利于發(fā)展學生運算素養(yǎng)。

（3）靈活運用條件，提高運算的簡潔性。

在教學過程中不僅要求學生會解數(shù)學題，更要讓學生學會觀察式子特征，力求簡潔，有利于培養(yǎng)學生的運算素養(yǎng)。

（二）在解決數(shù)學問題中，發(fā)展學生數(shù)學建模素養(yǎng)

“問題是數(shù)學的心臟”，解決數(shù)學問題是數(shù)學學習重要組成部分，也是學生學習數(shù)學的一個難點。因此在數(shù)學課堂教學中，教會學生將實際問題轉(zhuǎn)化成數(shù)學問題，并把問題加以解決，這就是數(shù)學建模。在初中的數(shù)學模型常見有以下：方程模型、函數(shù)模型、不等式模型、幾何模型、統(tǒng)計模型等

例3 小華叔叔開了一家公司，該公司去年的利潤為100萬元。今年總銷售價比去年增加了20%，總成本比去年減少了10%，今年的利潤為600萬元。求今年的總銷售價、總成本各是多少萬元？

分析：關鍵：找出等量關系。去年的總銷售價-去年的總成本=100萬元，今年的總銷售價-今年的總成本=600萬元。今年的總銷售價=去年總銷售價×（1+20%）今年的總成本=去年的總成本×（1-10%）

今年的總銷售價是2160萬元，今年的總成本1530萬元。

答：今年的總銷售價為2160萬元，今年的總成本為1530萬元。

分析：這是一道生活中有關利潤的實際問題，將實際問題轉(zhuǎn)化數(shù)學問題，根據(jù)題意選擇方程模型。既培養(yǎng)學生解決問題的能力，又激發(fā)學習數(shù)學的興趣，同時發(fā)展建模的素養(yǎng)。

要發(fā)展學生數(shù)學建模素養(yǎng)，首先突破學生對數(shù)學建模學習的思維障礙。在課堂教學中要留給學生足夠時間讀懂題意，教師要指導學生抓住題目關鍵的字眼，特別一些專門的術語理解。在課堂教學過程中要重視數(shù)學應用意識的培養(yǎng)，平時應加強聯(lián)系實際的教學，多開展一些“綜合與實踐”課題的教學。如“生活中的‘一次模型”這節(jié)綜合與實踐課，可以由學生展開調(diào)查，得到材料，利用所得材料，轉(zhuǎn)化數(shù)學問題，選擇恰當?shù)臄?shù)學模型，解決數(shù)學問題。學生得到材料不同，選擇模型也不同。有的學生選擇一元一次方程的模型，有的學生選擇一元一次不等式的模型，有的選擇一元函數(shù)的模型或者幾個模型綜合運用。在這一過程中學生經(jīng)歷把生活問題轉(zhuǎn)化成數(shù)學問題，為了解決這一問題就得選擇相對應數(shù)學模型，讓學生感受到數(shù)學就在自己的身邊，激發(fā)學生學習數(shù)學的積極性，發(fā)展學生的數(shù)學建模的素養(yǎng)。

例4 新開的服裝店，對某種品牌的服裝做試銷活動，每件服裝進價是100元，剛開始銷售時，服裝日銷售量y（件）是服裝日銷售價x（元）的一次函數(shù)。當x=120，y=80;當x=160，y=40。每件服裝的銷售價為多少元？此時每日最大銷售利潤是多少？

分析：這是一道生活中實際問題，將實際問題轉(zhuǎn)化數(shù)學問題，根據(jù)題意選擇函數(shù)模型。既培養(yǎng)學生解決問題的能力，又激發(fā)學習數(shù)學的興趣，同時發(fā)展學生數(shù)學建模的素養(yǎng)。

（三）在課堂中引導學生積極思考問題，發(fā)展學生邏輯推理的素養(yǎng)

數(shù)學課堂教學中不僅要注意解題策略，更要重視數(shù)學知識獲取的過程。數(shù)學邏輯思維能夠?qū)Ω拍钚纬伞⒚}推理等進行正確、合理的思考。所以不管是一個數(shù)學概念的形成，還是推理一個新命題。在課堂教學中一定要留給學生足夠的思考時間，才能碰發(fā)思維火花，培養(yǎng)學生邏輯推理的能力。教師在課堂教學中可以多問學生“怎樣想的”，開始他們是怎樣想的，但沒有想出來，后來又是怎樣想出來的，盡可能地讓學生暴露出他們的自己思維，充分發(fā)揮學生主觀能動性，讓學生從失敗中獲得成功的喜悅，這樣有利于學生激發(fā)學生學習數(shù)學積極性，發(fā)展學生邏輯推理的素養(yǎng)。

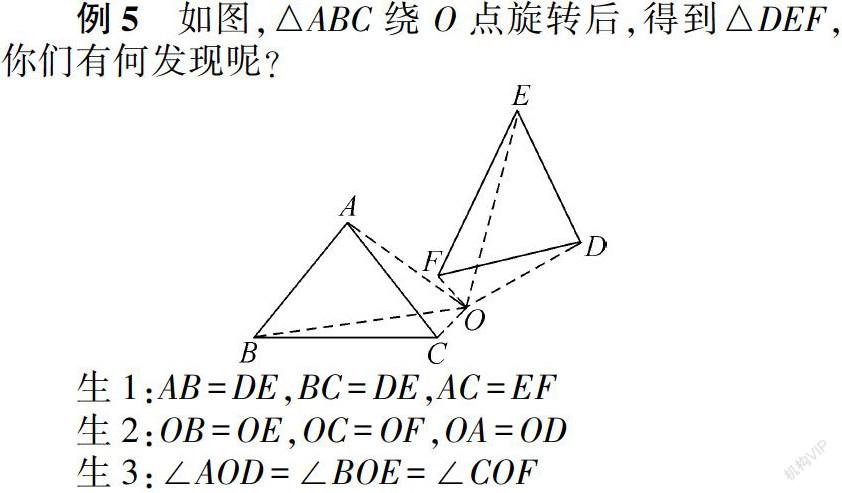
例5 如圖，△ABC繞O點旋轉(zhuǎn)后，得到△DEF，你們有何發(fā)現(xiàn)呢？

生1：AB=DE，BC=DE，AC=EF

生2：OB=OE，OC=OF，OA=OD

生3：∠AOD=∠BOE=∠COF

生4：旋轉(zhuǎn)前后的圖形全等;對應點到旋轉(zhuǎn)中心的距離相等;對應點與旋轉(zhuǎn)中心連線段的夾角等于旋轉(zhuǎn)角。

有效課堂教學應該是調(diào)動學生學習的積極性，啟動學生活躍的思維，隨時碰發(fā)智慧的火花，啟發(fā)學生積極思考。因此，留給學生足夠思考問題的時間，學生們主動參與課堂學習，既激發(fā)學生學習數(shù)學興趣，又培養(yǎng)學生邏輯推理能力。

（四）貫徹直觀性原則，培養(yǎng)學生數(shù)學抽象的素養(yǎng)

數(shù)學概念的學習是高度的抽象，而概念的學習是數(shù)學學習中不可缺少的一個重要環(huán)節(jié)。在概念教學過程中如何讓學生更好地理解概念，應用概念，發(fā)展學生抽象素養(yǎng)，是教師必須思考的問題。因此在概念教學過程中要利用好直觀性原則，有利于學生的學習。例如，學生學習“絕對值”這個概念時，可以利用數(shù)軸直觀性來揭示絕對值概念的本質(zhì)，激發(fā)學生的興趣。又如學習引入正負概念時，可以提供很多具有相反意義的量（如“加分與扣分”“盈利與虧損”“零上與零下”“上漲與下跌”）的現(xiàn)實模型。又如在上北師大版七年級上冊第一章《豐富的圖形世界》時，課前可以收集一些典型、有代表性的圖片，如古塔、金字塔、上海東方明珠塔等，并在課堂上用多媒體展示，與學生一起探討其中各部分的形狀，同時學生感知這些建筑物都是由許多幾何圖形組成，既激發(fā)學生學習主動性和積極性，又培養(yǎng)學生學生數(shù)學抽象能力。