運用思維導圖教學對初中代數CPFS結構影響的實驗研究

王雪倩 黃振坤

[摘? ?要]由概念域、概念系、命題域和命題系組成的CPFS 結構是數學中特有的認知結構，完整的CPFS 結構對學生的數學學習有較大的幫助;思維導圖被引入中國后至今已有不少人在各領域進行了研究并取得了較好的效果。研究表明，思維導圖在代數復習課中的應用能有效完善學生的代數CPFS結構，在代數復習課中運用思維導圖能幫助學生快速理清代數知識點之間的邏輯關系，從而提升教學效果，提高學生的學習成績。

[關鍵詞]思維導圖;CPFS結構;初中代數

[中圖分類號]? ? G633.6? ? ? ? [文獻標識碼]? ? A? ? ? ? [文章編號]? ? 1674-6058（2021）15-0032-02

一、問題的提出

新課標中強調了數學素養的地位，在文獻中喻平教授給出了數學中特有的CPFS結構，且經過諸多實證后，我們發現學生若能構建完整的CPFS結構，那么他們的數學理解能力、數學閱讀能力、數學解題能力等均會相應地提高。也就是說，CPFS結構能夠反映出學生整體的數學素養水平，且兩者呈正相關，CPFS結構為學生進行“數學理解”提供了更精準且有效的途徑：學生通過理解概念域、命題域中的等值關系和概念系、命題系中的幾種抽象關系，可以較準確且深刻地認識到“數學理解”中的各種聯系。由此可知，構建完整的CPFS結構對促進學生的數學學習具有重要的意義。

思維導圖以認知心理學為基礎，體現認知心理學的觀點，從知識的表現形式來看，可以非常直觀形象地表現出由事實、概念、命題以及原理所構成的知識網絡結構。作為一種元認知工具，它不僅可以很好地對知識的歸屬進行劃分（這也是它的基礎功能），而且可以將有的機械教學所導致的弊端轉變為學生主動去進行有意義的、高效率的學習。認知心理學認為，知識的本質在于概念和概念之間、命題和命題之間的內在聯系，我們對整個宇宙的認識，正是由反映概念與概念之間關系的復雜的概念結構系統構成的，而思維導圖將認知心理學的思想體現得淋漓盡致。

CPFS結構作為一種完整的數學學習認知結構，與思維導圖有著共同的理論基礎——認知心理學。基于此，筆者在猜想思維導圖與CPFS結構之間聯系的基礎上開展了本項研究，本文嘗試通過實驗，把在復習課中運用思維導圖的教學和一般教學對學生代數CPFS結構的影響進行對比研究，期望能夠得出一些有價值的結論，從而促進中學數學教學的發展，拓展有效教學的渠道。

二、研究意義及實驗方法、過程、結果

在理論上，本研究結合了思維導圖理論和CPFS結構理論，揭示了運用思維導圖進行代數復習課教學可提升學生代數CPFS結構的適用性和有效性，為初中一線教師實施中學數學教學提供一些理論上的支持，拓寬思維導圖在初中代數復習課當中的應用。

在實踐上，構建完整的CPFS結構對促進學生的數學學習具有重要作用，通過本實驗，探討促進中學數學復習課教學、優化課堂教學效果的教學模式。

1.實驗方法

實驗方法采用等組實驗法，在實驗班運用思維導圖進行代數復習課教學，在控制班采用傳統教學法，控制好實驗前兩班學生CPFS結構的水平、教師情況、測試材料等無關變量，實驗時間為一學期。

2.實驗過程

（1）被試

本次實驗選擇了廈門市某中學八年級4個平行班級的學生參加前測，根據前測結果選取出兩個水平最為接近的班級分別作為實驗班和控制班，每班各50人，實驗班為A班，控制班為B班。

（2）實驗安排

雖然本研究針對的是代數教學，但是自初二上學期開始，實驗班整個學期的復習課中均運用了思維導圖，目的是為了讓實驗班學生提前適應。進行實驗的時間按照學校正常的教學安排，測試時間均為自習課，且均為30分鐘。

3.結果與分析

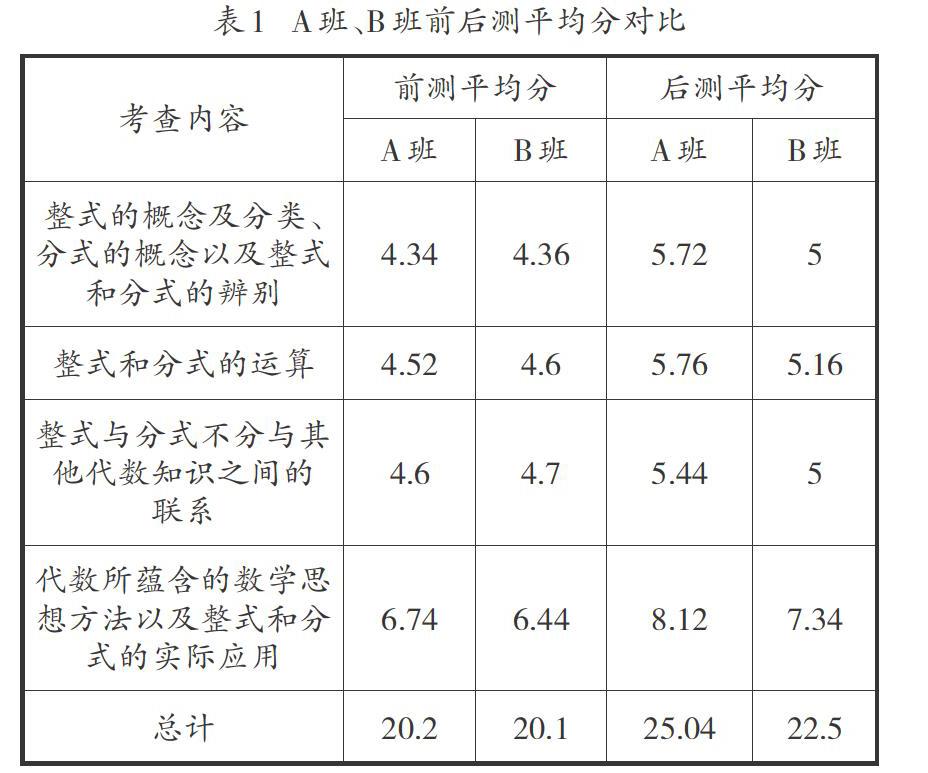
由表1和表2可知，A班和B班在各小題上的差異均不明顯，雙側T檢驗的P值為0.954>0.05，說明A班和B班的前測成績并無明顯區別，符合本實驗平行班的需求。參與實驗的兩個班級在前測中各部分平均分的差異均不是很明顯，后測中實驗班的成績明顯高于對照班，且從獨立性T檢驗結果來看，A班前后測雙側T檢驗的結果中P值為 0.006<0.05，B班P值為0.174>0.05，表明A班前測和后測的差異顯著，而B班前測和后測成績的差異并未達到統計意義上的顯著水平。

通過上述實驗及分析，可以得到以下結論：運用思維導圖進行代數復習課教學能夠構建學生的代數CPFS結構，且與一般教學相比較效果更好。

三、結論及建議

第一，思維導圖能夠激發學生的學習興趣。在運用思維導圖的實驗過程中，由于學生對新的教學方式很好奇，所以展現出極大的熱情，踴躍地和教師交流，積極性較高。在課堂上，實驗班的學生主動性更強，能夠自覺地思考和解答教師所提出的問題，說出自己的想法并與大家進行交流討論。所以，教師在教學中運用思維導圖，可以大大提升學生學習數學的熱情和積極性，從而教學效果和學生的學業成績也會相應得到改善。

第二，在代數復習課中運用思維導圖能夠完善學生的CPFS結構。從前測和后測的對比結果中可以看出，實驗班學生的思維方式和思維邏輯等都能得到不同程度的改進。在整個學習過程當中，學生加深了對知識的理解，鍛煉了發散性思維，在解答題目時能夠想到多種可能性，進而解決問題。

第三，運用思維導圖的代數復習課教學對于學生數學成績的提升效果更加明顯。從測試結果來看，實驗班和控制班前測結果并無明顯差異，經過復習課教學之后，雖然兩班成績都有所提升，但明顯實驗班提升幅度更大。

以上結果表明，代數復習課教學思維導圖可以完善學生的代數CPFS結構，也證實了在代數復習課教學中使用思維導圖的適用性和有效性，根據對實驗結果的分析，得出了以下幾點建議。

（1）思維導圖作為一種創新性思維工具，已經被應用得很廣泛，同時對使用者的思維也有一定要求，比如深度和廣度。此外，使用者還要大膽實踐、勇于突破、不斷進行創新，所以思維導圖可能更適合經驗豐富的教師使用。

（2）由于思維導圖是豐富多彩的，在應用時沒有統一的標準判定其對錯，所以教師對學生合理的想法要給予肯定，注意因人而異，對學生突如其來的想法也要充分包容。

（3）思維導圖作為信息技術的產物不是孤立存在的，它與很多其他教學辦公軟件之間都存在著聯系，在應用時要注意與PPT、Excel、幾何畫板等軟件相結合，使它的運用效用發揮到最大。

[? ?參? ?考? ?文? ?獻? ?]

[1]? 喻平.數學學習心理的 CPFS 結構理論[M].南寧：廣西教育出版社，2008.

[2]? 楊紅萍，喻平.個體CPFS結構與閱讀自我監控對數學閱讀的影響[J].數學教育學報，2011（5）：59-61+69.

[3]? 皮連生.教育心理學（第三版）[M].上海：上海教育出版社，2004.

（責任編輯? ? 黃諾依）