試談數形結合在數學教學中幾個“點”

張練

摘? 要：小學數學是小學眾多學科中非常重要的基礎應用學科，小學數學教學最根本就是要幫助學生認識數字和識別形狀。在小學數學教學實踐中，應用數形結合思想，將這兩個方面有機地融合在一起，可以產生很好的教學效果。本文總結了在小學數學教學中把抽象的概念直觀化、把算理算法規律形象化、把復雜的問題簡單化這幾條具體的應用策略，以幫助數學教師在教學實踐中有效的應用這一教學思想。

關鍵詞：數形結合;小學數學;應用

數形結合教學是小學數學教學中一個重要的教學方法之一，它能夠讓復雜變為簡單，讓抽象變為形象，讓繁瑣變為明朗，有助于幫助學生對數學概念的掌握和記憶，對解題思路的理清，對算理算法的理解，從而提高教數學教學質量。但如何利用好數形結合思想，結合自己多年的教學，就此談點看法。

一、找準數形結合的“切入點”? 讓概念問題變得“簡單化”

數學概念很抽象，而小學生畢竟由于年齡小，特別是低年級學生，抽象思維還在雛形階段，體現的大都是具體的形象思維，但在中高年級，隨著知識面的不斷擴大，數學概念的不斷增多，會不斷向抽象邏輯思維過渡，會出現一定的難度。也需要通過憑借事物的具體形象或表象來呈現。因此，我們在數學概念問題教學中，引入數形結合思想，找準數形結合的“切入點”，使學生對數學概念有著更加透徹的理解。比如，在學習什么是“三角形”的概念，書上表述為“由三條線段圍成的圖形，叫做三角形”，在教學時，如果教師單從只字面上去講解，學生不但難以理解，也無法形成正確的概念。所以就應該抓住“三條線段”和“圍成”字的切入點，在黑板上畫出三角形，讓學生指出哪是“三條線段”，怎么才能算“圍”，從圖形中把“三角形”的概念 “直觀化”，從“看”中在自己的頭腦中去形成“三角形”的概念，明確組成三角形的條件是三條邊的封閉圖形，理解“三角形”概念的真正涵義。然后，在黑板上在畫出一下是三角形或類似三角形圖形：

師：上面的圖形都是三角形嗎？

生：有些是，有些不是。

師：哪些是三角形？哪些不屬于三角形？

生：①③④是三角形，②⑤不是三角形

師：為什么？能說說理由嗎？

生：②沒有圍城，⑤三條邊不是線段。

師：對，看來同學生對三角形的概念已經理解。

在這里，學生對三角形的涵義已經掌握，理解了三角形的本質屬性，通過這樣數形結合的教學方式，學生對數學知識會有更加深入的理解，課堂教學的效果會非常理想。

二、把握數形結合的“契合點”讓算理問題變得“清晰化”

在數學計算環節教學中，算法算理是教學中的一個難點，如何讓學生更容易對算理的接受、理解和運用，這是我們在教學中要深入思考和積極探索的問題。在教學中，滲透數形結合思想，運用數形結合的方法，把握準數形結合的“契合點”，能夠很好地讓學生理解和掌握算理。

如在教學“兩位數乘兩位數的筆算”整堂課的教學過程中，無論是理解題意、口算和筆算，還是理解算法和算理，都利用點子圖來進行輔助教學，將抽象的數字形象化，將具體的計算步驟直觀化，將繁雜的計算方法具體化，將難懂的算理清晰化，更便于學生對新知識的理解和掌握。因此在計算教學時用“數形結合”的方法，有利于中低年級段的學生掌握算法理解算理。

比如：計算14×12

師：在計算14×12的過程中，我們得到這樣的四個數： 8、20、40、100

師：你們能在點子圖中找到它們嗎？

學生在點子圖中找出四個數所在位置，教師課件展示。（如下圖）

師：（在圖中將8個點和20個點圈起來）圈起來的部分對應豎式中的哪部分？

生：28

師：這個28是哪兩個數的乘積？

生：14×2的積

師：28是幾套書的本數？

生：2套書的本數。

師：（在圖中將40個點和100個點圈起來）這又對應著豎式中的哪個部分？

生：140

師：它是哪兩個數的乘積？

生：14×10的積

師：是幾套書的本數呢？

生：10套書的本數。

師：最后我們把28和140相加，得到168。168是哪兩個數的乘積？

生：14×12的積。

師：也就是幾套書的本數？

生：12套書的本數。

在這里，借助點子圖這個“契合點”，進行“數”與“形”的結合來講清楚算理，這種直觀表象形式，表示豎式中相對應的數字，同時把豎式中的數字在點子圖中找出對應的部分，整個教學環節形象直觀，激發學生的學習興趣，提高了學生的抽象思維能力。數形結合的方法，有利于學生直觀地理解算法和算理。

三、尋求數形結合的“突破點”讓應用問題變得“直觀化”

應用數學解決實際問題既是數學的特點， 也是學習數學的目的之一。解決實際應用問題，比如“行程問題”“植樹問題”“工程問題”等等，在平常的教學中，一般都是讓學生審題，找出已知條件，理清數量關系， 然后進行解答，這對題目比較簡單的學生都容易進行直接解答，但對比較難的應用問題，學生往往無從入手，所以，這就需要充分利用數形結合思想，尋求它的“突破點”，通過數與形之間的相互轉化，通過數形結合化“抽象”為“直觀”，通過線段圖，從線段圖中進行比較，直觀地發現數量之間存在的聯系，從而分析解決問題的思路方法。

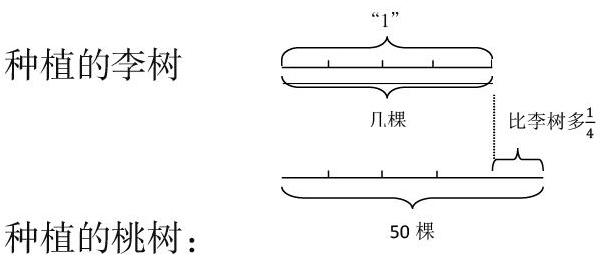
例如，小明的爺爺在果園種植果樹，種了桃樹50課，種的桃樹比種的李樹多1/4，爺爺一共種了多少棵果樹？

這道題對判斷誰是單位“1”有一定的困難，誰比誰多了幾棵沒有明確數據，該用乘還是除，很多學生難以理解題目的真正意思，易混淆分數乘除法，學生難以進行解答。這時，如果老師不失時機滲透數形結合的思想方法，找出“突破點”，引導學生依據題意畫出相應的線段圖，讓學生一目了然的知道種的桃樹比種的李樹多，并多了1/4，才能幫助學生迅速找出等量關系列出方程，通過線段圖寫出等量關系式：種植李樹的棵樹+比種植李樹多1/4?桃樹的棵樹=種植桃樹的棵樹，求出種植李樹的棵樹，然后在求出一共的棵樹就容易解決了。單位“1”是種植李樹的棵樹，可以用方程解：設種植李樹的棵樹為“X”，列式.X+1/4X=50，解得X=40，即種植李樹的棵樹為40棵，爺爺在果園里一共種植了90棵果樹。

這里，通過數形結合，從“突破點”入手，準確的找到數量之間的聯系，進行比較、分析，得出算式，解答出要求的問題，這里實際上就是把復雜、抽象的問題形象化，變得“簡單”明了，降低題目的難度，加深了學生的理解，這樣不僅提高了學生的發散思維能力，還培養學生的數形轉換能力和多角度思考問題的能力。

總之，在數學教學中，幫助學生解答相關的問題，需要充分發掘“數”與“形”的本職聯系，利用數形結合思維，去努力探索分析問題和解答問題，掌握算法算理、解題技巧，培養學生的數學思維，提高學生學習數學的興趣與積極性。

參考文獻

[1]劉敬娟.“數形結合”思想在小學數學教學中的滲透[J].新課程（小學）.2015年12期.

[2]陳水秀.對小學數學教學中數形結合思維運用探究[J].課程教育研究.2019年11期.

[3]廉萌.“數形結合”思想在小學數學教學中的應用[J].青少年日記（教育教學研究）.2019年04期.

[4]趙靜.小學數學教學中數形結合思維運用探究[J].科學咨詢（教育科研）.2018年08期.

[5]對小學數學教學中數形結合思想的分析[J].數學大世界（上旬）.2019年02期.

[6]數形結合，理解算理——數形結合在小學高段數學教學中的運用[J].新課程（小學）.2019年06期.

[7]“數形結合”在小學數學教學中的運用策略探討[J].新課程（小學）.2018年12期.

[8]“數形結合”思想在小學數學教學中的應用分析[J].中國校外教育.2018年33期.

龍巖師范附屬小學