轉化思想在小學數學“空間與圖形”教學中的運用探究
陳詠
摘 要:在解決數學問題的過程中,經常會應用轉化思想。在小學數學“空間與圖形”的教學過程中應用轉化思想,能夠幫助學生降低學習難度,同時豐富學生的解題思路,促使學生加深理解。在教學中教師應積極引導學生應用轉化思想分析和解決問題,提升“空間與圖形”教學的質量和效果。基于此,文章分析了轉化思想的具體運用措施,希望對廣大教師的教學有所幫助。
關鍵詞:轉化思想;小學數學;空間與圖形;運用措施
中圖分類號:G623.5?文獻標識碼:A?文章編號:2095-624X(2021)05-0023-02
新知識的學習,是通過對舊知識的發展和轉化來實現的。在小學數學“空間與圖形”教學中合理運用轉化思想,有助于教學質量和教學效果的提升。但是目前部分教師對轉化思想的認識和實施存在一定的不足,基于此,本文就轉化思想在小學數學“空間與圖形”教學中的運用措施進行探究,僅供大家參考。
一、在小學數學“空間與圖形”教學中運用轉化思想的意義
(一)有助于提升教學質量
小學數學是學生學習數學知識的起步階段,也是學生掌握數學學習方法的關鍵時期。轉化思想普遍存在于小學數學教材中,例如,在進行平面圖形面積公式的推導過程中,通過對圖形的平移、旋轉以及割補等,將圖形轉化為熟悉的圖形,進而推導出平面圖形的面積公式。這既能幫助學生加深理解,也能使學生將各種平面圖形面積公式有機地聯系起來。同時轉化思想還可以幫助學生更加靈活有效地解決問題,促使學生通過不同的方法來解決問題,促進學生思維能力的提升,起到培養學生數學素養的作用。在“空間與圖形”教學過程中運用轉化思想,能夠幫助學生構建完善的知識體系,促進教學質量的提升。
(二)有助于學生掌握數學思想方法
在小學數學教材中,蘊含多種數學思想方法,比如數形結合思想、分類思想、函數思想等,轉化思想是其中一種比較常見的思想方法。尤其在“空間與圖形”這部分內容中,轉化思想的體現更為廣泛,同時也滲透著其他數學思想,但是轉化思想是其他思想方法的重要基礎。在教學中合理運用轉化思想,能夠使學生加深對數學思想方法的認識和理解,其不僅可以幫助學生掌握轉化思想方法,而且還有利于學生理解和掌握其他數學思想方法,進而促進學生數學素養的提升,為學生后續的學習奠定基礎。
(三)有助于提升學生的思維能力
通常情況下,學生的學習往往只停留在知識層面,如果學生掌握了數學思想,則可以在很大程度上提升數學思維能力,進而促使其自身解決問題的能力得到提升。學生所學的數學知識有可能會忘記,但他們所掌握的數學思想以及數學思維方法會使其終身受益。轉化思想不僅是一種解題的方法,更是一種重要的數學思想。轉化思想可以幫助學生將數學知識轉化為數學能力,這對提升學生的數學素養以及促進學生的全面發展具有十分重要的意義。運用數學思想,能夠促進學生抽象思維能力的提升,提升學生思維的深刻性與靈活性。
二、轉化思想在小學數學“空間與圖形”教學中的運用措施
(一)深入挖掘
轉化思想貫穿于“空間與圖形”教學的全過程,雖然教材中并未將轉化思想單獨提出來,但是教師應在教學的各個環節中注重滲透轉化思想,充分體現轉化思想的作用和價值,幫助學生更好地掌握和理解相關知識。轉化思想是人們在探索數學知識的過程中逐漸積累形成的數學思想方法,并且蘊含在小學數學教材中,尤其在“空間與圖形”中,轉化思想無處不在。要想實現對轉化思想的充分滲透,教師需要深入挖掘教材中蘊含的轉化思想。教師在“空間與圖形”的教學過程中,應對教材中的素材進行深入分析,挖掘其中的轉化思想,并在教學中有意識地滲透轉化思想,這樣才能取得更好的教學效果。對轉化思想的挖掘,不應局限于教材,教師還需要注重從生活中提取、挖掘素材,使教學更貼近學生生活,使學生更容易理解轉化思想。
(二)精選方法
小學生仍以具體形象思維為主,并在學習過程中逐步提升抽象邏輯思維能力,因此在小學數學“空間與圖形”這部分內容的教學過程中,教師應通過直觀的方法滲透轉化思想,這樣才能更容易被學生所接受,同時也能降低學生理解和掌握轉化思想的難度。教師可以在教學過程中應用生動有趣的圖表或者動態演示畫面,將抽象的數學知識轉化為更加直觀、具體的形式呈現給學生,這種方式更加符合小學生的特點,有助于提升教學的有效性。近年來,多媒體在教學中的應用越來越廣泛,多媒體能將數學知識轉化為動態的畫面,更好地營造相應的情境。在“空間與圖形”教學中應用多媒體,是體現轉化思想的教學手段。例如,在講解“圓的面積”這部分內容的過程中,教師便可以充分利用多媒體進行教學。首先制作多媒體課件,將圓平均分成32份,然后將其轉化成長方形或者是平行四邊形,并在教學過程中應用多媒體向學生呈現這一轉化過程,幫助學生加深理解“圓的面積”這部分知識,同時也能使學生加深對轉化思想的理解和認識。
(三)合理運用轉化思想
轉化思想的應用貫穿于教學的整個過程。首先,可以在知識形成過程中應用轉化思想。例如在“不規則圖形面積”這部分知識的教學過程中,教師應引導學生思考將不規則圖形轉化為規則圖形,進而求出不規則圖形的面積。在教師的引導下,學生可以通過割補以及剪拼等方面來實現圖形的轉化,可以將不規則圖形轉化為長方形或者是正方形等規則圖形,進而結合長方形或者正方形面積公式來求出不規則圖形的面積。在知識形成過程中引導學生應用轉化思想,能夠幫助學生更好地掌握新知識。
其次,在動手操作過程中運用轉化思想。現代教學更加注重理論聯系實際,尤其對于小學生而言,動手操作是其獲取知識的重要方式。相較于其他方面的數學知識,“空間與圖形”具有更強的操作性,通過學生的動手操作,可以使學生認識到這部分知識與現實生活之間的聯系。同時動手操作也能充分體現學生的主體性,有助于提升學生自主學習的質量與效果。學生的動手操作包括拼一拼、擺一擺、剪一剪等,這些活動都是對轉化思想的運用,既能幫助學生更好地掌握相關知識,也能促使學生加深對轉化思想的認識。引導學生動手操作,并不只是為了幫助學生獲取知識,同時還要幫助學生加深對數學思想的領悟。以“梯形面積公式”這一內容的教學為例,教師可以引導學生動手操作,通過拼一拼,將兩個梯形拼成一個平行四邊形,求出平行四邊形的面積再除以2便可以得出梯形的面積。教師也可以引導學生畫一畫,用虛線延伸梯形的兩個側邊,進而形成一個大的三角形。這樣,只要求出大三角形和小三角形的面積,然后用大三角形面積減去小三角形面積便可以得出梯形的面積。通過動手操作,親歷轉化全過程的方式,可以使學生加深對知識內在聯系的理解。
最后,在問題解決過程中運用轉化思想。幫助學生理解和掌握轉化思想,目的在于運用,只有學生能夠靈活運用轉化思想,才能真正發揮出轉化思想的作用和價值。同時,也只有在運用的過程中才能促使轉化思想真正內化為學生的知識和能力。因此,教師應引導學生在解決問題過程中積極運用轉化思想。以“平行四邊形面積”這一內容的教學為例,教師可以引導學生將平行四邊形轉化為長方形,然后應用長方形面積來求出平行四邊形的面積。再比如,在講解“三角形面積”這一內容的過程中,教師可以引導學生將三角形轉化為平行四邊形。這樣,既能使學生認識到轉化思想在解決數學問題中的重要作用,也能加強知識之間的內在聯系,有助于學生構建完整的知識體系。
(四)加強訓練
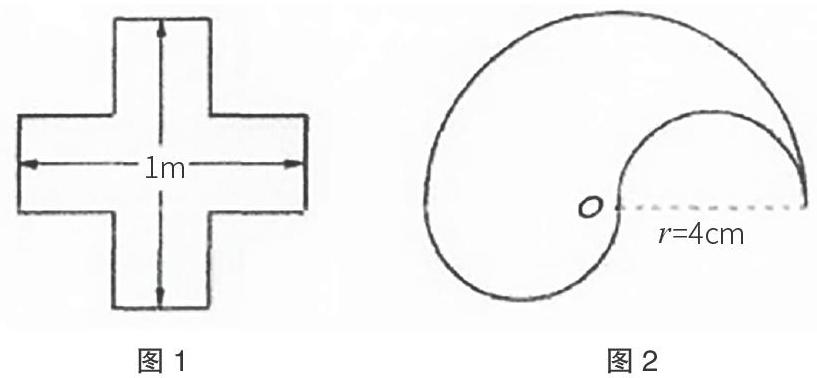
在“空間與圖形”的教學過程中,教師應注重向學生滲透轉化思想的重要作用,使學生加深對轉化思想的認識,提升學生運用轉化思想的積極性。比如在講解“三角形內角和”這部分知識的過程中,可以將三角形的三個內角轉化成為一個平角,幫助學生加深理解。同時,教師還要向學生強調,新知識的學習是對舊知識的延伸和轉化,學習的過程是舊知識轉化為新知識的過程,讓學生對轉化思想有更深刻的理解和認識。在教學中滲透轉化思想,需要經歷一個長時間不間斷的過程,同時也需要經過反復的訓練,這樣才能使學生加深領悟。教師的引導,能夠幫助學生初步感悟轉化思想,而要想使其轉化為學生內在的能力,則需要加強訓練,訓練的主要方式便是解題。學生解題的過程便是運用轉化思想的過程,同時也是加深對轉化思想認識的過程。教師可以結合轉化思想設計習題,這樣能夠提升習題的針對性,幫助學生更好地理解和掌握轉化思想。例如,計算圖1和圖2兩個圖形的周長。
這兩個圖形屬于不規則圖形,要想計算出圖形的周長,需要學生應用轉化思想。圖1,學生可以將其轉化為邊長為1m的正方形,這樣便很容易計算出周長。圖2,學生可以將其轉化成一個半徑為4cm的半圓和一個直徑為4cm的圓,這樣一來便很容易計算出周長。面對這樣的題目,學生在解題過程中必然會應用到轉化思想,因此可以實現對轉化思想的訓練。
結語
在小學數學教材中蘊含著豐富的轉化思想,尤其在“空間與圖形”這部分內容中,轉化思想貫穿始終。在教學中合理運用轉化思想,可以幫助學生更好地理解和掌握數學知識,并且能夠促使轉化思想內化為學生自身的能力,使學生能夠更好地應用轉化思想解決數學問題,提升學生的數學素養。
[參考文獻]
[1]劉長福.在小學數學“空間與圖形”教學中滲透轉化思想[J].科學咨詢(教育科研),2014(2):77-78.
[2]高翠玲.淺談小學數學教學中轉化思想的滲透[J].延邊教育學院學報,2019(6):245-246.
[3]林麗琴.轉化思想在小學數學教學中的運用——以“圖形與幾何”教學為例[J].福建教育學院學報,2019(2):91-93.
作者簡介:陳 詠(1977— ),女,江蘇沛縣人,中小學一級教師,專科,研究方向:小學數學教學。

