巧用思維可視化優化數學概念教學

【摘要】本文論述利用思維可視化促進學生理解數學概念的策略，提出巧借思維可視化促進概念教學的具象化、結構化和模型化，依據概念特征用好思維可視化工具，巧用思維可視化優化數學概念教學結構等教學建議，以讓看不見的思維路徑顯現化，更好地服務于教師的教和學生的學，提升小學數學概念教學質量。

【關鍵詞】小學數學 數學概念 思維可視化

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2021）09-0134-02

所謂思維可視化就是把看不見的思維路徑顯性化，一般借助圖示、動作、文字、符號等來實現。思維可視化不僅是一種教學行為，更是一種教學理念，它主要以讓學生“直觀地看、形象地畫、出聲地想”等來實現思維可視化的目的。概念教學是小學數學教學的重要組成部分，在以往的教學中，教師大都采取讓學生死記硬背概念的做法讓學生機械地記憶，導致學生對概念的理解不深，難以把握概念的本質，直接影響了數學學習質量的提升。那么，在小學數學概念教學中，怎樣才能借助思維可視化來優化學生的概念學習呢？

一、巧借思維可視化，促進概念教學具象化、結構化和模型化

基于數學概念的本質特點，教師可以采用“情境—直觀—操作”等方法引導學生學習數學概念，讓學生經歷概念的形成與演化過程，進而掌握概念的本質意義。

（一）借思維可視化促進概念教學具象化

為了使學生深刻地理解和認知數學概念，教師要還原概念生成的全過程，讓學生突破概念理解的難點，但由于學生在概念理解中經常出現思維斷層現象，實施思維可視化策略可以幫助學生跨越思維斷層，促使概念教學具象化，進而促進學生對概念意義的理解。如在教學“分數的概念”時，對三年級學生來說理解分數的概念有一定的困難，這就需要教師為學生提供直觀的模型，為學生搭建看得見、摸得著的思維支架，以幫助學生把抽象的分數和具體的圖形聯系起來，使得分數概念形象化，促進學生對分數概念的理解與認識。

（二）借思維可視化促進概念知識結構化

借助思維可視化可以幫助學生把“點狀”的單個概念知識連向“網狀”的知識結構。如在“周長和面積”的概念教學中，學生很容易混淆周長和面積的概念，這時候教師就可以對“邊長為4分米的正方形，面積與周長相等”展開辨析教學，讓學生通過動手畫一畫、列表比一比等可視化操作活動來幫助學生發現周長與面積之間的聯系與區別，從而形成比較完善的知識結構。

（三）借思維可視化讓數學概念經驗模型化

在數學概念教學中，采用思維可視化策略不僅能對學生的數學認知結構產生一定的作用，而且在數學活動經驗模型化上也有一定的意義。如在教學“面積的概念”時，借助思維可視化策略可以讓學生經歷從定性到定量的認知過程，使學生對“度量”的要素有一個整體把握，幫助學生真正建構“度量”的經驗模型。

二、依據概念特性，用好思維可視化工具

基于數學概念的特點和學生的理解水平，在概念教學中，常用的思維可視化工具主要有以下三種：

（一）學習概念前的圖示工具——喚醒經驗

在學生學習數學概念前的思維可視化工具就是指基于學生生活經驗與現實情境緊密結合的圖示工具，它的一般表現形式為生活場景圖或者實物圖。如在“周長”的概念教學中，由于學生對周長已經有了一些模糊的前概念認知，平時也接觸過不少與周長有關的情境，比如在體育課上沿著操場跑一圈，沿著邊沿剪紙等活動經驗，教學時教師就可以把生活中的“周長”形態進行動態演示，以激活學生的生活經驗，幫助學生建立“一周”的表象認知，促進學生對周長概念的理解。

（二）概念學習中的圖示工具——聚焦本質

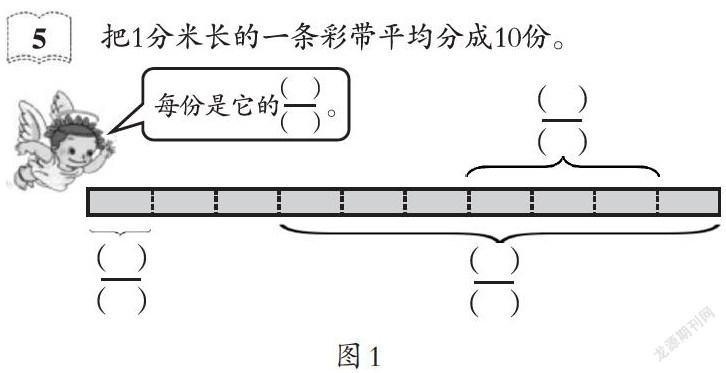
學生在概念學習過程中運用的圖示工具，一般是以單點結構圖示為主，單點結構的圖示指向的是概念的本質屬性。以直觀模型為例，它作為常用的可視化思維工具之一，可以是面積模型，也可以是線段模型、集合模型等。這些模型的圖示結構大都比較簡單，以“平均分”這個數學概念為例，在認識十分之幾的分數時，就可以以1分米長的紙帶作為學習工具。（如圖1）

這樣從部分到整體，學生對幾分之幾也就會有更加直觀的認識與理解。

（三）概念學習后的圖示工具——厘清關系

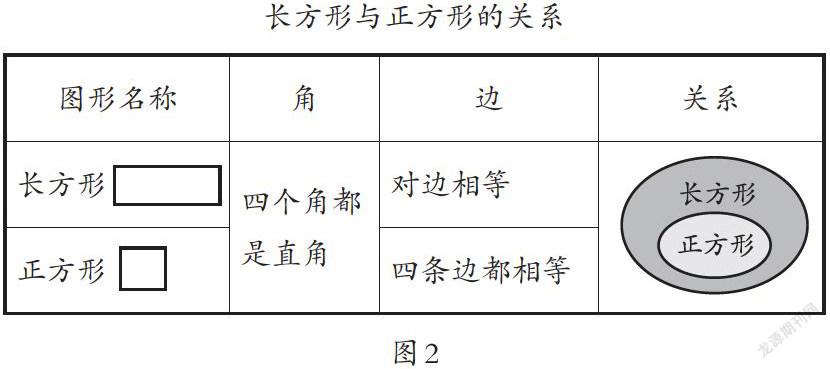
概念學習后的圖示工具大都是以多點結構為主，作為多點結構的圖示工具，其重點在于幫助學生溝通知識之間的聯系，并能夠在學生知識的生長點上進行重點標注，以達到幫助學生厘清知識之間關系的目的。如在“四邊形”的認識教學中，教師就可以采取讓學生對圖形進行分類、比較、歸納、概括等方法，以幫助學生歸納概括出四邊形各種類型的特征，并把學生的目光聚焦到長方形與正方形的再認識上。（如圖2）

這樣引領學生學習數學概念，思維可視、直觀清晰，學生對概念的理解和認識也會更加深刻。

三、巧借思維可視化，優化數學概念教學結構

在指向思維可視化的概念教學中，教師可采用“原型重現—初建表象—表征內化—結構完善”等方法，幫助學生真正經歷概念的形成過程，優化數學概念教學的結構，進而達到概念建構的目的。

（一）鏈接生活經驗，搭建思維可視化支架，優化概念教學

在概念教學的起始階段，思維可視化主要體現在與學生生活經驗的對接上，它的主要表現形式是以“直觀地看”為主。如對“分數的認識”中的“分數”來說，它的原型為“平均分物”，教師可以以“分蛋糕”作為學生的生活對接原型展開教學：首先，教師出示情境圖，讓學生思考“4個蛋糕平均分給2個人，每個人分到幾個？2個蛋糕呢？1個蛋糕呢？你能用合適的數分別表示平均分的結果嗎？”以喚醒學生已有的生活經驗。其次，教師再借助課件向學生動態展示分蛋糕的畫面，讓學生對分數有一個初步的感悟，并結合平均分1個蛋糕的動畫演示，理解“半個→1/2個”“1/3個”“1/4個”是多大。在這個過程中，教師像引入自然數一樣引入分數，借助平均分的生活原型，喚醒學生對已有生活經驗中分蛋糕的認知。為了幫助學生初步認識分數，積累等分經驗，教師可讓學生參與“1/2個、1/3個、1/4個的實物模型”的創造，以使學生對分數的意義有更為直觀的認識，這樣在具體“平均分”的可視化情境中，學生對分數的概念印象深刻。

（二）提供表象支撐，促進思維可視化，深化數學概念教學

在概念教學中，當學生初識概念之后，概念就會以一定的表象在學生的頭腦編碼中儲存起來，給學生以心理圖示。這時候教師如果能夠以單點結構圖示或者多點結構圖示的形式給學生進行可視化展示，使學生真正經歷“直觀地想、形象地畫”等可視化學習過程，進而促進概念教學的表象化，深化概念教學。

如在“1厘米”這個數學概念建構的過程中，教師就可以借助尺子這種可視化思維工具進行教學：首先，教師可以讓學生仔細觀察尺子，并告訴學生這把尺子上有許多1厘米，看看你能夠找出多少個1厘米。其次，讓學生回想一下生活中的1厘米，讓學生說說哪些物體的長度或者厚度可能是1厘米。最后，再讓學生閉目想象1厘米有多長，用手比劃一下或者徒手畫一畫。這樣以找、比、想、畫等可視化的方式引領學生學習，可以物化學生對1厘米的認知，化抽象為具體，幫助學生建立對1厘米的表象認知。

（三）借思維可視化，完善概念結構體系，提升概念教學實質

在概念教學中，要想幫助學生深化對概念的認知，還需要對學生的概念認知結構不斷完善，形成概念網。

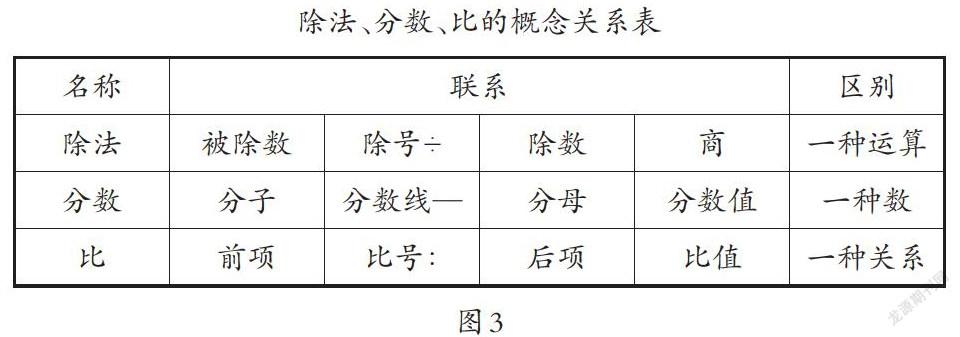
如在學習“比”這部分內容之后，為了使學生對“除法”“分數”“比”這三者的特點和區別有進一步的理解與認識，教師可以通過圖表來幫助學生梳理清楚這三者之間的關系。（如圖3）

這樣充分利用表格，學生對除法、分數和比之間的聯系與區別有清楚地感知，真正實現了概念意義的建構和概念體系的建構，提升了概念教學的質量。

總之，在指向思維可視化的小學數學概念教學中，教師要更新觀念，認真鉆研教材文本，在把握概念本質特點的基礎上，把握好思維可視化在概念教學中的落點，為學生的思維可視化搭建適切的支架，注重對學生思維可視化學習過程的指導，以達到優化概念教學、提升數學教學質量的目的。

【作者簡介】李清（1972— ），女，廣西興業人，大學專科學歷，一級教師，主要從事小學數學教學與研究。

（責編 林 劍）