三種教材“銳角三角函數”概念獲得的對比研究
奚雯燕


[摘? 要] 文章分別對蘇教版、人教版、浙教版銳角三角函數概念的獲得做了對比,在比較的基礎上提出相應的教學建議.
[關鍵詞] 教材對比;銳角三角函數;概念;整合
銳角三角函數是初中數學內容的重要章節.一方面是在學習了直角三角形兩銳角關系、勾股定理、相似三角形等知識的基礎上,對直角三角形邊角關系的進一步深入和拓展研究;另一方面,又為解直角三角形等奠定了基礎.本節課不僅有著廣泛的實際應用,而且起著承前啟后的作用.
三種教材對“銳角三角函數”
概念獲得的對比研究
1. 蘇教版教材的編排
某體育館為了方便觀眾,設計了不同坡度的臺階.
【觀察與思考】
(1)哪個臺階更陡?
(2)下面哪個臺階最陡?你是如何判斷的?
(3)比較兩個臺階,你有什么發現?
一般地,如果銳角A的大小確定,我們可以作出Rt△AB1C1,Rt△AB2C2,Rt△AB3C3…
分析:教材提供了三個問題,引導學生從實際問題的幾何直觀逐步過渡到對抽象圖形的數學思考:第一個問題主要基于幾何直觀判斷臺階哪個更陡;第二個問題則是提供了三個不同直角邊長的三角形(抽象的臺階),感受直角三角形的直角邊的長度會影響臺階“陡的程度”,將直觀感受過渡到量的刻畫,尋找數學語言描述陡與緩.一種是通過斜面與水平面的夾角大小描述,夾角大則陡;另一種是通過邊的比較描述,例如①與②水平長度相同,高越大,臺階越陡,②與③高度相同,水平長度越短,臺階越陡,于是三個臺階中②最陡,但是剩下兩個臺階誰更陡,暫時還解決不了.也就是當水平長度之間、高度之間都不相同時,怎么比較臺階陡與緩,需要進一步探究.第三個問題是基于(2)中未解決的問題作的鋪墊,發現兩個三角形相似,對應角相等,臺階的傾斜程度一樣.但是教材到這里,就把正切的概念引出來,筆者認為有點突然.對于教材(3)中的問題,發現當角確定時,邊的比值也隨之確定,把這個確定的比值叫角的正切,似乎前面解決臺階的傾斜程度完全沒有必要.既然問題已經提出,解決(3)之后,可以繼續探究(2)中①與③的傾斜程度.既然相似不改變傾斜程度,那么相似就成為①與③傾斜程度比較的橋梁.通過相似,將①與③其中一個圖形進行放縮,使得放縮以后的圖形與另一個圖形水平長度或者高相同,這樣就能比較出放縮以后的圖形與另一個圖形的傾斜程度,從而能比較①與③傾斜程度.這個過程是本節課最精彩的地方,讓學生進一步感受除了斜面與水平面的夾角大小可以刻畫傾斜程度,高度與水平長度的比也可以刻畫傾斜程度.前者的經驗,孩子在生活中已經具備,后者經驗的獲得是本節課的重點也是難點.在這個過程中發現夾角確定,高度與水平長度的比也隨之確定,為了表示兩者之間的這種關系,引入符號tan,給出名稱,這種關系就是函數關系,但三角函數這個詞要到正弦、余弦講完之后才真正給出.在兩課時學習過程中,先認識三角函數中的部分(正切、正弦、余弦),再認識整體(三角函數),是不利于學生理解函數這個模型的.
2. 人教版教材的編排
問題:為了綠化荒山,某地打算從位于山腳下的機井房沿著山坡鋪設水管.在山坡上修建一座揚水站. 對坡面的綠地進行噴灌,觀測得斜坡的坡角(∠A)為30°,為使出水口的高度為35 m,需要準備多長的水管?
思考1:在上面的問題中,如果出水口的高度為50 m,那么需要準備多長的水管?
這就是說,在Rt△ABC中,當銳角A的度數一定時,無論這個直角三角形大小如何,∠A的對邊與斜邊的比都是一個固定值.
分析:教材問題從現實生活中引入,體現了數學服務于生活. 思考1是利用“直角三角形30度角所對直角邊是斜邊的一半”解決問題,本質上是讓學生感悟無論直角三角形大小如何,當一個角為30°時,這個角的對邊與斜邊的比始終等于,是一個定值.思考2借助勾股定理可以發現,無論直角三角形大小如何,當一個角為45°時,這個角的對邊與斜邊的比始終等于,是一個定值. 探究的目的是為了將從特殊情況下得到的結論推廣到一般并進行證明. 與蘇教版不同的是,人教版三角函數中第一個學習的是正弦,而蘇教版第一個學習的是正切,先學哪一個并不重要. 人教版研究的問題指向性更強,始終圍繞銳角、對邊、斜邊這三個量展開,從特殊角的對邊與斜邊比值固定推廣到一般情況,先易后難,符合學生的認知規律. 但結論推廣的過程有些快,在解決完思考之后,教材就把探究問題給了出來,缺少類比聯想的過程. 每一個問題的產生都是基于觀察、發現. 學生產生問題的能力普遍低于解決問題的能力,能力的培養應該貫穿在整個教學過程中. 筆者認為在思考2之后,也可以讓學生說一說前面我們在研究什么問題,后面可能會研究什么問題,可以采用怎樣的研究方法.讓學生學會研究數學的方法遠比解決單個問題更有價值.對于銳角A仍然可以賦值,比如50°等,讓學生畫圖、量長度、計算、猜想,并用幾何畫板進行動態演示. 讓學生經歷從特殊到一般,猜想、歸納、證明的完整過程.
3. 浙教版教材的編排
兩個物體在傾斜角不同的斜面上向上運動相同的距離,它們上升的高度相同嗎?
在傾斜角(∠α,∠β)不同的兩個斜面上,物體前進的距離都是1,而它在水平和鉛垂兩個方向上運動的距離卻各不相同. 物體在斜面上運動時,在斜面上所經過的距離和水平方向、鉛垂方向經過的距離,與斜面的傾斜角之間有什么關系呢?
合作學習:
通過上面兩個實踐操作你發現了什么?
分析:教材從學生已有的知識基礎和生活經驗出發,明確本節課將圍繞角的大小與邊比值的關系展開研究. 合作學習過程從特殊到一般,符合學生的認知規律.通過回憶熟悉的定理,讓學生明白直角三角形中銳角與邊比值存在關系,并大膽猜測直角三角形中任意角α的對邊與斜邊比值是否固定. 在探索比值的相關量的過程中,發現比值隨角度變化而變化,從而使學生初步形成銳角三角函數的概念,巧妙地把三角函數放在函數的概念體系中進行教學,讓學生體會了銳角三角函數產生的必要性. 對照函數概念進一步確認角度是自變量,比值是因變量,突破難點;在動手操作的過程中,讓學生參與知識形成的全過程. 浙教版教材最大的亮點是第一課就把銳角三角函數的概念給出,這與蘇教版和人教版不同.在過程性方面,浙教版在第一課時主要圍繞銳角三角函數存在的必要性展開,為什么我們要學習銳角三角函數,是基于怎么樣的情境去進行這樣的探究,更體現了學習數學的價值,展示了研究數學問題的一般方法,具有示范性. 但不足之處在于,既然研究比值,那么三條邊可以產生六個比值,為什么只研究了一部分,從銳角三角函數的概念來講并不完整.
三種教材對“銳角三角函數”概
念獲得的教學設計整合
銳角三角函數編排在“函數”和“相似三角形”之后,在概念的獲得過程中用相似的知識進行證明.作為本章的起始課,筆者認為定位應該更高些,將研究銳角與邊的關系的必要性交代清楚.在探究關系的過程中,不斷并反復讓學生感悟到直角三角形中銳角確定,邊的比值隨之確定這個事實,喚起記憶,讓學生關系借助已有學習經驗,生成新知.每一版教材編寫都有自己的設計意圖.作為教師,我們不是教教材,而是用好教材,重組教學活動,優化教學路徑,引導學生找到知識的生長點和延伸點.結合各版本,筆者對銳角三角函數概念的引入進行了如下教學設計,僅供參考.
環節1:引入課題
問題1:直角三角形的兩個銳角之間有什么關系?
問題2:直角三角形的三邊之間存在怎樣的關系?
問題3:在直角三角形中,我們已經知道了邊的關系、角的關系,接下來我們要研究什么關系?
設計意圖:啟發學生認識到直角三角形的邊的關系和角的關系是分離的,各自有自己的關系,還沒有研究直角三角形中邊與角的關系.因此,研究直角三角形中邊與角的關系是擺在師生面前的共同問題,是必須要解決的問題,即“直角三角形的邊角關系是什么”是這節課要研究的問題.
環節2:引出比值
問題4:在Rt△ABC中,∠C=90°,∠A=30°,AB=10,則BC等于多少?
問題5:你能快速解決這個問題的依據是什么?
設計意圖:從角與邊,過渡到邊的比值.
問題7:直角三角形3條邊,兩兩組合有多少種?
設計意圖:從一個比值過渡到初中階段的三個比值.
活動1:填表(Rt△ABC,∠C=90°)
設計意圖:對于含有30°、45°的直角三角形,讓學生初步體會“角度固定,比值也固定”,為后面猜想作鋪墊.
環節3:探索角與邊之比的對應關系
問題9:當∠A為30°、45°時,表格里的比值是固定值,那么當∠A取其他銳角時,比值是否也固定呢?
設計意圖:從特殊角過渡到一般角(具體度數),進一步強化“角度固定,比值也固定”的結論.
師生活動:在操作過程中,每個人取的B點并不一樣,但是分別比較接近,但又不完全一樣,因為得到數據的方式是測量,測量會產生誤差. 幾何畫板演示分兩個階段,第一步在∠A一邊上移動點B,即改變直角三角形的大小,讓學生進一步體驗到“角度固定,比值也固定”;第二步改變射線AB的位置,讓學生體會到“角度改變,比值也改變”,每一個固定的∠A,都有唯一確定的比值與之對應,可使其對后面的函數有更直觀的理解.
設計意圖:通過幾何畫板演示,初步確認猜想的正確性,體會角度與比值之間的對應關系.
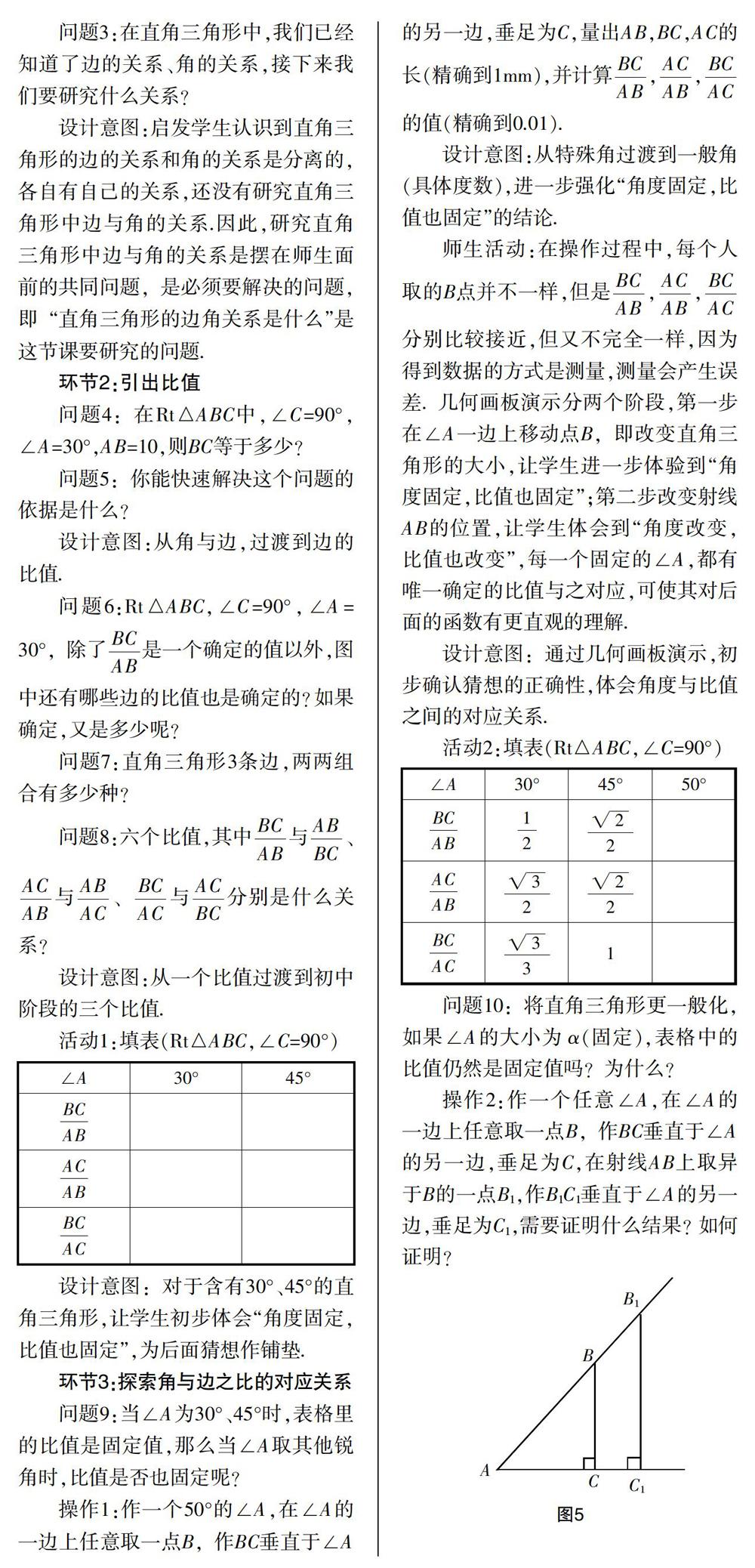
活動2:填表(Rt△ABC,∠C=90°)
問題10:將直角三角形更一般化,如果∠A的大小為α(固定),表格中的比值仍然是固定值嗎?為什么?
操作2:作一個任意∠A,在∠A的一邊上任意取一點B,作BC垂直于∠A的另一邊,垂足為C,在射線AB上取異于B的一點B1,作B1C1垂直于∠A的另一邊,垂足為C1,需要證明什么結果?如何證明?
設計意圖:這個操作設計可以由學生完成,如果學生想不到,教師可以借助在幾何畫板中的拖動效果加以引導,讓學生完成作圖. 同時加深學生對“角度固定,比值也固定”的理解;猜想的證明過程又可以培養學生的推理論證意識.
設計意圖:得出結論“角度固定,比值也固定” .
設計意圖:得出結論“角度變,比值也變” .
環節4:引出銳角三角函數概念
活動3:填表(Rt△ABC,∠C=90°)
設計意圖:引出正弦、余弦、正切和銳角三角函數概念,并引入符號表示.
整合教材的啟示
每一版教材各有千秋,每一位研究者站在不同的角度,看待問題也會有不同的結果.整合教材不是對原本教材的否定,而是在已有教材的基礎上再創造. 教材整合是一個動態的過程,是教師立足于真實課堂教學情境,基于自身教學經驗,以教材為依托的自我建構過程.進行教材整合的前提是要跳出教材,站在教材之上.作為一名教師,要想跳出教材,就要認真鉆研教材. 教師要認真研究教材編寫的意圖、每個環節的目的,挖掘開發課程資源,對教材精心“加工”. “加工”的度要符合學生的實際,適合學生的發展. 能讓學生最大化地實現學習目標的“加工”,就是有效“加工”.

