初中數學教學要注重“問題意識”
曾世光
【摘要】初中學生在數學的學習中,普遍存在著成績提高慢、知識掌握不牢固、習題練習錯誤率高等現象,降低了學生的學習效率。針對以上情況,筆者以學生學習中存在的問題為出發點,進行了詳細的研究并提出了相應的改正措施,為提高初中生學習效率起到了一定的輔助作用。
【關鍵詞】初中數學;學習效率;提高;輔助作用
數學知識是學生們學習階段的重點學習內容,在初中教育大綱中占其有一定的分量。由于數學知識的抽象性和邏輯性較強,對于部分學生來說這具有一定的困難,使學生們意識上產生了枯燥厭倦的感覺,不利于學生的學習。[1]作為新時代下的初中數學教師,筆者在日常的數學教學中,重視學生學習中存在的細節問題,并根據具體情況提出了改進的措施,為提高學生的數學學習效率打下扎實的基礎。
一、聚焦細節問題,培養學生嚴謹態度
初中學生由于年齡問題,性格上還處于天真活潑的階段,對事物充滿好奇心。因此,初中學生在數學的學習上普遍存在著容易馬虎,缺乏嚴謹的學習態度等現象,成為了數學考試中成績提高的“絆腳石”。我在數學的課堂上,注重學生的學習態度問題,通過細節問題作為切入點,來提高學生的學習嚴謹態度。
例如,人教版初中數學《一元二次方程》知識中,本課知識是數學知識的基礎。學生在學習此節課時,對于一元二次方程中計算的部分掌握得還可以,但在實際問題中的應用就顯得略有不足。究其原因由于學生審題不認真導致忽略細節等錯誤。針對此現象,我在課堂上著重培養了學生的嚴謹的態度,讓其在今后的學習中避免再因為馬虎而丟掉分數。
例題1:某服裝店新進一款衣服,每天可以賣20件,每件可盈利44元,現在每件降價在10元以內,如果每件下調1元,那么每天比原來多賣5件,請同學們分析一下:如果老板想每天盈利1600元,那么每件衣服應該降價多少錢呢?
學生們在解這道題時,很容易忽略已知條件“每件降價在10元以內”在設出了X后,列出了關系式,得出了結論x=4,x=36,會有一部分學生選擇36這個答案。筆者在講解時,讓學生們注意細節的重要性,培養學生的嚴謹的學習態度,有效降低了學生的習題練習中的錯誤率發生。
二、重視概念問題,提升學生基礎水平
初中數學知識是離不開概念的支撐的,數學概念是數學學習的基礎,是學生理解分析數學問題的保障。目前,初中學生的數學學習中,普遍存在著解題思路窄,對問題缺乏解題方向的判斷能力,錯誤率高。究其原因,其與學生的基礎概念掌握程度不夠牢固具有一定的關系。[2]筆者在數學課堂的習題講解中,重視學生的概念的應用,強化學生對知識的記憶理解程度。
例如,人教版初中數學《平行四邊形》一課中,本課是幾何知識中的基礎,由于平行四邊形具有的抽象性,成為部分學生學習中的軟肋。這除了是學生的自身的抽象能力原因外,還和學生對數學概念的掌握不牢固有一定的關系。筆者在例題講解時,會融入概念的知識,進一步提高學生的學習效率。
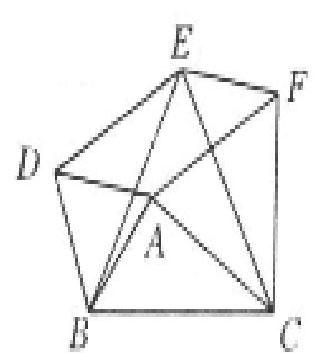
例題2.如右圖現有△ABD、△AFC、△ECB,三個等邊三角形分別建立在△ABC的各個邊上,現將E、F、A、D四點相連接,請同學們進行證明:四邊形ADEF是平行四邊形。
本題看似紛亂無章,但是根據全等三角形和平行四邊形的概念及性質進行切入,其答案便會很容易求得。筆者在講解時分別將相關的概念進行了重新的闡述,然后讓同學們再進行解題的思考,學生們很快便找到了此題的關鍵點。通過概念的引入,可以使學生頓悟解題的思路,找到解決問題的正確方法,提高了學生的解題速度。
三、注重數形問題,提高學生抽象能力
數學知識由計算部分和幾何部分組成,主要需要學生調動抽象思維和邏輯思維能力來進行知識的學習。[3]筆者在學生的學習教學中,倡導學生進數形結合的方法來分析問題,將抽象的知識有效轉化為直觀的數學知識,降低學生的解題難度。
例如,人教版初中數學《弧長和扇形面積》知識中,本課知識點難度較高,是學生們學習中的難點所在。筆者在這部分的練習題中,鼓勵學生進圖形的配合,將抽象的知識進行了直觀的轉化。
例3.飯店的圓桌半徑為60厘米并且可坐八個人,每個人距離桌子大約10厘米。現在增加兩人,已知:10人的距離與原8個人的距離相等,請同學們進行計算,每個人向后挪動了多少厘米?”
此題難度較高,抽象性較強,如果導入圖形模型后,便可直觀地看出“10個人之間的距離與8個人的距離相等”的意思是圓周上兩個人之間的圓弧的長度是相等的,此題解決難度便大大下降,學生們設出了未知數為X后,便可以輕松列出算式?最后求得答案x=17.5。
數形結法就是應對此類問題迎刃而解的有效方法,其降低了抽象問題的難度,對學生有頓悟的作用,使學生迅速找到解決問題的突破口,為提高學生的解題速度起到了不可替代的作用。
四、小結
初中數學在學生的其他各學科學習中占有重要的比例,是學生學習其他知識的基礎。因此,教師在教學中不但要重視學生成績的提高,還要關注學生的學習能力的培養,針對學生學習中的存在的不足,因而進行對癥下藥,為提高學生的數學學習效率打下扎實的基礎。
【參考文獻】
[1]趙永利.中學數學教學中問題情境的創設與運用[J].數學學習與研究.?2019(22)
[2]李昌官.數學抽象及其教學[J].?數學教育學報.?2017(04)
[3]何向東.基于數形結合提升學生數學思維能力的策略[J].學周刊.?2020(05)

