基于“導問”的高中數學教學設計策略

【摘 要】新高考命題聚焦對學生關鍵能力的考查，特別強調要使學生在深刻理解的基礎上對知識融會貫通、靈活運用。在課堂教學中，通過導問，以問題串的形式引導學生進行主動探究和深層次學習，有助于學生深刻領會概念的內涵與外延，在自主建構概念的過程中提升創新思維能力，在自主解決問題的過程中養成科學思維的習慣，在自主發問中形成批判性思維意識。

【關鍵詞】導問；創新思維；科學思維；批判思維

【中圖分類號】G633.6? 【文獻標志碼】A? 【文章編號】1005-6009（2022）67-0011-04

【作者簡介】朱曉祥，江蘇省木瀆高級中學（江蘇蘇州，215101）教師，高級教師。

高中數學教學應以發展學生數學學科核心素養為導向，創設合適的教學情境，啟發學生思考，引導學生把握數學內容的本質。導問式教學是以“導問”為特征的一種課堂教學活動，是以“問題鏈”的形式，讓學生在學習中層層交流、深入思考，進而能主動發問。導問式教學設計的問題應該具有以下三個特點：一是具有引導意義的問題情境；二是有目的地發展學生的認知策略；三是讓學生感知數學方法論的出發點。因此，導問式教學方式有助于發展學生的創新思維能力，培養嚴謹求實的科學精神，樹立敢于質疑、善于思考的批判性思維意識。下面，筆者以具體的教學實例，談一談如何設計基于“導問”的高中數學課堂教學。

一、以“問”導“建”，在自主建構概念中培養學生的創新思維能力

數學概念是揭示現實世界空間形式與數量關系本質屬性的思維形式，是數學知識的基本單元。因此，在概念教學中，通過“導問”引導學生積極參與數學概念的建構過程，有利于學生更好地理解其實質，也有利于對學生科學思維能力的培養。筆者在執教人教A版高中數學必修第二冊第六章第一節“平面向量的概念”時，進行了以下探索和思考，與同行們交流。

筆者認為，本節課的目標主要有三個：一是讓學生抽象出向量的基本概念、基本表示、研究特殊向量之間的基本關系；二是理解平面向量的幾何意義和代數意義，體會數形結合的數學思想；三是讓學生體驗研究新概念的基本思路和內容，即通過類比、抽象、概括、歸納、實踐等途徑，研究一個新概念的定義、表示、關系和應用。因此，在設計“問題鏈”時，應該設置有引導意義的問題情境，通過啟發式的引問幫助學生建立認知結構。

【教學片段一】

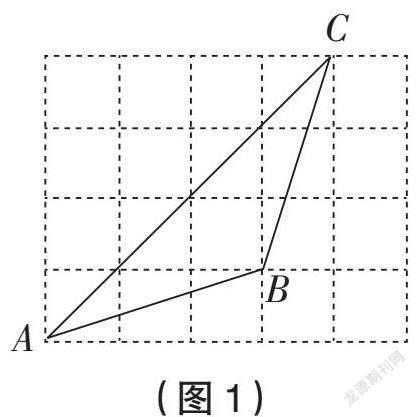
問題1：如圖1，若小正方形的邊長為1m，一只螞蟻沿直線從A爬行到B，再從B爬行到C。螞蟻爬行的距離和位移分別是多少？

問題2：距離和位移有什么不同？

問題3：位移作為一個物理量，它同時包含大小和方向兩個要素，請列舉生活中的位移。

問題4：這一類對象的共同屬性是什么？你能用數學的語言概括“向量”的概念嗎？

問題5：在數學學習的過程中，我們有沒有學過既有大小、又有方向的量？

問題6：我們學過類比數、集合、函數的研究方法，接下來我們應該從哪些方面研究向量這一新的概念？

問題1從實際生活中的情境出發，引導學生感悟兩個不同的概念，引出向量概念的原型；問題2培養學生的抽象概括能力和語言表達能力；問題3引導學生觀察、概括，得到概念的本質屬性；問題4引導學生自主生成概念；問題5將物理模型數學化；問題6在問題5的基礎上層層設問，讓學生體會研究概念的基本途徑，培養學生的科學思維。

基于問題解決取向的教學模式，強調在教學過程中利用“問題鏈”將學生的概念表象與原有經驗聯系起來，在設置導問和問題解決過程中給學生更多的獨立空間。在教學中，處于中心地位的應該是通過問題解決的過程發展學生的元認知策略、認知結構和相應的學習態度。

二、以“問”導“思”，在自主解決問題中培養學生的科學思維方式

美國心理學家紐厄爾與西蒙（Newell & Simon）提出：問題是這樣一個情境，個體想做某件事，但不能即刻知道做這件事所需采取的一系列行動。［1］當學生遇到難度較大的數學題時，需要有適切的解決問題的策略和合理而科學的思考過程。在這個過程中，教師通過“導問”提出具有探究性的問題，將突破點設置在學生的思維最近發展區，調動其解決問題的欲望，這有助于培養學生的自主意識和創新意識。

數學問題解決的過程應該分為以下五個階段。（1）理解問題：什么是未知的？什么是給出的？（2）問題表征：代數表征和幾何表征是什么？（3）拆分成子問題。（4）實施：確定計算和推理過程。（5）反思：問題的內涵和外延。

在人教A版高中數學選擇性必修第一冊第二章“直線和圓的方程”的學習中，學生遇到這樣一個問題：已知a＞0，過點P（a，[3]a）的直線l與x軸、y軸交于A，B兩點，且△AOB面積為8[3]，這樣的直線有4條，求a的取值范圍。

這道題對學生來說有一定的難度，其難度來自兩個方面：一是與學生既定狀態已掌握的知識和技能的聯系較少；二是題目的表征形式的一般化程度不高，具有一定的抽象性。基于這樣的情況，筆者設置了以下導問路徑。

【教學片段二】

問題1：已知條件是什么？求什么？

問題2：過一點的直線由什么元素確定？

問題3：怎樣從代數的角度表達“這樣的直線有4條”？

問題4：（追問）你能夠構建解題過程嗎？

問題5：怎樣從幾何的角度表達“這樣的直線有4條”？

問題6：同學們是否記得在之前的學習過程中我們做過這樣一道題：過點P（2，2[3]）的直線l與x軸、y軸的正半軸交于A，B兩點，求△AOB面積的最小值及此時直線的斜率。

問題7：我們能否將點P一般化，得到一般性結論？

在這個問題鏈中，問題1、2是提出問題，問題3是代數表征，問題5是幾何表征，問題4是選擇解決問題的一個策略，問題6是局部啟發，問題7是反思和應用。本教學環節以問題為起點，以探究為路徑，創造適合學生思考的合作環境，從而喚起學生對問題及其本質的探究欲望。

三、以“問”導“問”，在自主發問中培養學生的批判性思維意識

在數學教學中，我們不僅要讓學生成為“問題解決者”，還要讓學生成為“問題發現者”，讓學生主導問題的提出、問題的分析、問題的解決三個課堂環節。

1.引導學生追因索果，由疑生問

在數學教學過程中，我們希望學生對所學的知識和方法，不僅要知其然，更要知其所以然。因此，在教學過程中，要讓學生學會多問為什么，努力激發學生提問的意識。

在處理這個問題的過程中，生1的方法通過多項式乘法原理解決問題，其實是對二項式定理的認知，體現了較強的元認知能力和批判性思維能力。學生2改編的變式題拓寬了“三項”向“二項”轉換的途徑，體現了較強的創新意識。學生在自主發問和反思中探究了這一類問題的本質——“三項”轉換為“二項”。

2.引導學生自編習題，由問生思

問題解決是一個發現、探索和創新的過程，包括提出問題、建構模型、設計方法、檢驗反思等。學生作為課堂的主體，應成為問題的發起點和終結點，讓學習真正發生。在課堂上引導學生自主發問甚至是自主編題，有利于培養學生的高階思維能力和批判性思維。

【教學片段四】

在“直線和圓的方程”單元復習課中，筆者編制了這樣一道復習題：過點P（3，1）作圓C：（x-1）2+y2=1的兩條切線，切點分別為A，B，求切線PA的長。

師：以此為條件，你認為我們可以研究哪些問題？請你把問題編寫完整，并嘗試解答。

生1：求線段AB的長。

生2：可以從角度看，求∠APB的大小。

生3：還可以從面積的角度探究，求四邊形PACB的面積。

生4：求[PA]·[PB]的值。

師：總結一下，剛才四位同學分別從幾何圖形中的線段長度、角度大小、面積大小、向量數量積四個方面編制了四個題目，請同學們課后自行完成這四個題目。這是一個幾何圖形中的定態問題，有沒有同學可以將這道題目改編成動態狀態下的取值范圍問題？

生5：可以將點改成動點，點P為直線x+y-4=0上的動點，過P點作圓C：（x-1）2+y2=1的兩條切線，切點分別為A、B。

師：非常好，以下是老師編寫的幾道習題，請同學們思考并完成。從線段長度的角度：（1）求切線PA的最小值；（2）求線段AB的最小值。從角度大小的角度：（1）求∠APB的最大值；（2）圓C上存在點N，使∠CPN=30°，求此時P點橫坐標的取值范圍；（3）當∠APB=60°時，求點P的坐標。從面積的角度：求四邊形PACB面積的最小值。從向量的角度：求[PA]·[PB]的最小值。

（學生完成練習）

師：點P是一個動點，它使得圖形中一些幾何元素的取值發生了變化，從而產生了以上一些有關取值范圍問題。同學們能否探究一下，當點P在直線上移動時，幾何圖形中是否有確定的量或者幾何元素？編制一道定點定值的習題。

生6：可以探究直線AB是否過定點以及△PAB的外接圓是否過定點。

在數學學習中，要徹底理解一個數學問題，就要弄清楚它的“來龍去脈”。在平常教學過程中，尤其是章節復習課和習題課中，教師首先應留時間給學生，鼓勵學生大膽嘗試，增強學生的學習信心和發問意識；其次是要把握好問題的“發問點”，精心挑選題干，讓學生有題可編，有問可發，從而使學生的發問意識、批判意識在數學課上得到鍛煉和提升。

新課程強調對學生創新意識和創新思維的培養。在數學課堂教學中，教師要關注與創新相關的能力和素養的培養，比如獨立思考的能力、發散性思維、逆向思維等，關注學生發現問題和批判性思維的能力，培養學生探索新方法、積極主動解決問題的能力，擺脫思維定式，勇于創新。通過“導問式”的課堂模式，引導學生思考，培養學生的關鍵能力和核心素養。

【參考文獻】

［1］鐘啟泉，徐斌艷.數學教育展望［M］.上海： 華東師范大學出版社，2001：10.

［2］教育部.普通高中數學課程標準（2017年版2020年修訂）［S］.北京： 人民教育出版社，2020：5.

［3］李紅婷.數學問題解決教學設計及其實施策略［J］. 數學通報，2007（6）：34-37.

［4］趙士元.導問：讓思維成長——以一道高三數學難題的教學為例［J］. 江蘇教育，2018（35）：39-42.