好問題驅動好課堂

翁海芳

[摘? 要] 創新作為數學學科最根本的核心素養，主要表現在能不能提出有質量的問題上. 現結合一堂“圖形和坐標”復習課實例，探討如何實現問題驅動課堂教學，從而讓學生既增長知識，又在創新能力上有所深化.

[關鍵詞] 初中數學;問題驅動;課堂教學

創新意識和創新能力是數學學科最根本的核心素養，而創新意識和創新能力主要表現在能不能“提出問題—提出好問題—提出有價值的問題—提出能夠推動數學發展的問題”上. 在我區的一次教研活動中，一位年輕教師展示了一堂“圖形與坐標”（浙教版八年級上冊第四章）復習課，整節課的問題由學生提出，提出的問題也由學生解決. 問題驅動、活動推動、情思涌動，讓課堂精彩不斷，課后學生意猶未盡，聽課教師也深受感染. 筆者現將課例展現如下，與同行共同研討.

教學實錄

師：圖形是幾何范疇的，坐標是代數范疇的，聯系這兩者的載體是平面直角坐標系. 這節課我們就從最簡單的幾何圖形“點”出發，共同回顧“圖形與坐標”這章內容.

環節1 如圖1所示，在平面直角坐標系中，已知點A的坐標為（-2，1），請問你能提出哪些數學問題？（要求問題簡潔，考查的知識點不要重復，不能在問題中增加其他的點）

生1：點A在第幾象限？（每個象限點的符號都有什么特征？）

生2：點A到x軸的距離是多少？（到y軸的距離呢？）

生3：點A關于x軸的對稱點是什么？（關于對稱點，我們總結出來的規律是什么？）

生4：點A關于一三象限角平分線的對稱點是什么？

生5：點A向下平移三個單位得到的點的坐標是什么？（平移的規律是什么？）

學生提出了前面的問題，教師順勢補充了后面（括號里）的問題. 通過第一環節的追問，本章的知識點在學生的腦海里逐步呈現了，喚醒了學生的思維.

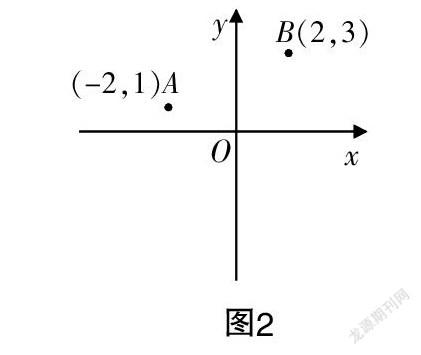
環節2 如圖2所示，我們從一點出發提出了有關點的位置問題（靜態的）和有關點的變換問題（動態的），現在增加一個點B（2，3），你又能提出哪些問題？

生6：求線段AB的長度. （構造直角三角形，利用勾股定理求解）

生7：求線段AB的中點坐標.

……

通過環節2的問題的提出和解決，點燃了學生的思維.

環節3 兩點確定一條線段后，我們可以解決線段的長度和中點坐標的問題，如圖3所示，如果再增加一個點C（a，0），你又能提出哪些問題？

師：這個點C和A，B相比有什么區別？（動點和定點），點C在哪里動？（x軸上）

生8：當△ABC的面積為5時，求a的值.

生9：當△ABC為等腰三角形時，求a的值.

生10：當△ABC是直角三角形時，求a的值.

生11：當△ABC的周長最小時，求a的值.

整堂課在學生不斷提問和解答的過程中氣氛高漲，最后進入了環節4.

環節4 如圖4所示，當平面直角坐標系中有三個點時，同學們就提出了很多有關三角形的問題——有關形狀的、面積的、周長的，現在再增加一個點D（a+1，0），你還能提出什么問題呢？

生12：求四邊形ABCD周長的最小值！

師：這個問題難度較大，它出現在近幾年的中考壓軸題中，因為時間關系，這個問題就留給大家課后思考吧！

教學點評

縱觀整節課的教學設計，環節1給出了一個平面直角坐標系和一個點A，讓學生回顧此章的基礎知識：點的坐標在每個象限內的特征;點到x軸、y軸的距離;點關于x軸、y軸對稱點的特征;點的平移規律等基本知識點. 環節2增加了一個點，在平面直角坐標系中已知兩點，學生自然就想到了求線段長度以及求線段中點坐標等問題. 在教師的引導下，師生共同推導了相關的公式. 環節3又增加了一個動點C，學生自然地想到求最小值的問題. 由于三個點可能組成三角形，就特殊三角形提出了問題. 環節4再增加了一個點D，把本節課推向了高潮. 學生的情緒高漲，提出的問題是“求四邊形ABCD周長的最小值”，此時教師點撥：“只要求出AC+BD的最小值，就可以求四邊形ABCD周長的最小值.” 由于時間關系，將本問題放在課后讓學生自主探索. 而這類問題，在近幾年的中考壓軸題中經常出現.

本堂課從最基本的點出發，延伸到線，拓展到面，從零散的知識演變，生成中考壓軸題考查的內容，環環相扣，層層遞進，渾然一體. 復習課不再是知識的再現，不再是要點的羅列，不再是解題技巧的灌輸，而是通過學生的自主提問，把整章需要復習的知識要點都融入了進來，學生弄清了知識發生的來龍去脈，形成了重要的結論和解決問題的方法，并且思維始終處于積極的狀態，圓滿地實現了一堂高效復習課的目標. 為什么本節課能夠實現以學生提出的問題推動整堂課的步步深入？主要是做好了以下三點：

1. 巧妙的預設讓課堂有聲有色

整節課教師只出示了四個點，但這四個點坐標的設置，教師之前是經過深思熟慮的. 第一個點（點A）在第二象限;第二個點（點B）與第一個點的橫坐標互為相反數，落在第一象限;第三個點（點C）是x軸上的動點. 這樣的安排給學生留足了空間，學生可以充分發揮自己的想象，通過舊知回顧，提出了有一定深度的問題. 當時聽課的教師既驚訝學生能夠提出這么多好問題，又感嘆執教教師膽子真大，在公開課上也會如此冒險，潛臺詞是“萬一學生提出的問題太難，課堂上解決不了怎么辦”. 據筆者事后了解，本堂課之所以如此流暢，不是因為師生課前經過排練上了一堂表演課，而是因為教師基于學情作出了科學安排：學生在前學段已經學習了直角三角形、等腰三角形等特殊三角形的知識，但還沒有學習相似、一次函數等內容;在平時的課堂上，學生初步感受過把幾何圖形放在平面直角坐標系中去解決，但沒有深入. 教師認為學生會基于本章的知識點當堂提出問題，即使結合前面所學的特殊三角形，也能做到由學生提出、由學生解決. 一般不會出現漫無邊際、束手無策、無法達到復習目標這樣的極端情況. 教師通過巧妙的預設為學生搭臺，以學生為主體的課堂最終呈現出了“百花齊放，青勝于藍”的效果.

2. 合理的引導讓課堂有邊有界

課堂演變中，當教師給出了點A的坐標（-2，1）時，有學生提出了“求線段AO的長”這一問題. 教師馬上引導，讓學生注意到“不能在問題中增加其他的點”這一條件，還讓學生注意到“要區分靜止的點和運動的點”兩種情況. 學生也就領會到“原來求線段長的問題我們暫時還不能提”. 如果點A是一個靜止的點，就往坐標特征方面進行探索;如果點A是一個動點，就向軸對稱變換和平移變換方面進行探索. 在環節3中，有學生提出了“當△ABC是等腰三角形時，求點C的坐標”這一問題，教師馬上表揚了這個學生，并及時引導其他學生思考：“除了等腰三角形外，還有哪些特殊三角形？”學生就向直角三角形等方向進行了拓展，一步步推動思維走向深入. 整節課中，教師隨時關注著學生的信息，在一些關鍵的節點給予引導或點撥，既提高了課堂的教學效率，又把握了引導的尺度，真正讓每位學生站在了研究者的角度深入其境，感受到了學習的樂趣.

3. 華麗的轉身讓課堂有質有量

本節課做到了四個轉身：一是教的轉身. 教師的角色從知識的傳授者轉變為了學生學習的組織者、引導者、合作者，在課堂上除了認真聆聽學生提出的問題外，還適時引導學生解決這些問題. 二是學的轉身. 學生的角色從“學會”轉變為了“會學”，“跟老師學”轉變為了“自主學”. 學生不是停留在學會課本知識的層面上，而是站在研究者的角度深入其境;不是簡單地“學”數學，而是深層次地探究以前學過的知識來提出高質量的問題. 三是課堂氛圍的轉身. 過程以“流暢、開放、合作、‘隱’導”為基本特征，教師盡可能減少對學生思維活動的干預，教學過程呈現了一種比較流暢的特征，整個情境以學生與學生、學生與教師之間的“對話”“討論”為出發點，以互助、合作為手段，以提出問題、解決問題為目的，讓學生在一個較寬松的環境中自主選擇獲得成功的方向，判斷發現的價值. 四是評價的轉身. 教師對學生的評價沒有停留在學習結果的關注上，而是更加關注學生提出問題的過程，從而培養學生學習的興趣，幫助學生認識自我，獲得廣泛的數學經驗.

教學感悟

（1）問題驅動教學是一個不斷“生長”問題和解決問題的過程，起于問題的開發，終于問題的解決. 驅動學生積極主動地參與學習的全過程，得到提出問題、分析問題、解決問題的能力，從而促進學生全面發展，發展和挖掘學生的各種潛力，激發學生思考，學會終身學習的本領. 教學中充分尊重和發揮學生的主體地位和作用，增加學生的主觀能動性和合作精神，促進思維的發展，使學生真正成為學習的主人;而教師作為教學活動的參與者、管理者和調控者，與學生構成互動、互助、互相啟發的態勢，以驅動整個學習活動順利完成.

（2）問題驅動教學對教師提出了更高的要求，教師不僅要知識淵博，還要具備洞悉學生心理、思維特點的能力，更要有靈活駕馭課堂教學的能力，能組織好課堂教學，促進學生提高問題意識和探索能力. 關鍵還要把握好四個“度”：把握好問題的難度，設計的問題要控制在學生認知的最近發展區;把握好問題的梯度，讓學生如上樓梯一般在不知不覺中向高處登攀;把握好問題的密度，讓課堂提問“四兩撥千斤”，發揮最好的效果;把握好問題的角度，多個角度設計問題，培養學生的核心素養.

（3）問題驅動教學并非僅是教師設計問題、提出問題，學生解決問題，還包括學生發現問題、提出問題，由此來啟發學生的創造性思維，提高他們的創新能力，完成一個“學生質疑—教師參與解疑—學生釋疑”的完整過程，這是我們今后努力的方向.