呈現關聯思維，優化數學課堂

俞曉婷

【摘 要】小學數學關聯教學，根據知識之間橫向與縱向的內在聯結，教師可以給予適當的方法結構指導，幫助學生建構完整的數學知識體系。在關注知識關聯的同時，更要注重學生學習方法結構的關聯，以促進學生“深度學習”為教學出發點，以提高學生學科核心素養為最高目標。本文以案例為分析載體，具體說明方法結構的可行性操作。

【關鍵詞】小學數學 關聯教學 方法結構 數學核心素養 深度學習

在聯結心理學的影響下，傳統的數學教學一般都是以分—分—總的形式開展，學生通過反復練習掌握所學內容，繼而達到“鞏固”“提升”的目的。整個學習過程中，學生獲得的知識是“散裝”的、閉塞的，學生腦海中沒有形成閉環的知識體系。學生對知識的認知失去整體架構與結構的關聯，對知識的認識僅僅停留在點狀層面，這導致學生在學習新知時處于被動狀態，缺乏學習的主動性。這不僅會影響學生掌握知識，對后續的知識遷移也有負面的影響。教師只有幫助學生架構起一座“知識的方法結構橋梁”，關注學科知識、認知與思維內外縱橫的結構關聯，讓學生經歷建構的過程，促進“深度學習”的自然發生，才能提高學生的數學核心素養。

“深度學習”是指教師作為學習的引領者，幫助學生投入其感興趣的、具有挑戰性的學習活動，從而使其身心得到發展，認知得到拓展，進而體驗到成功的、有意義的學習活動。換句話說，“深度學習”應該是幫助學生自主探究，在已有知識結構的基礎上，根據新知的情境進行有方向的知識遷移，從而發現數學知識的核心本質的探究過程。小學數學“深度學習”是以小學生數的認識、符號的認識、數的運算、數量關系、圖形的認識、圖形的測量等能力的發展為中心，基于核心內容選擇“深度學習”的主題。教師引領學生積極參與相關內容的學習的建構過程。

華東師范大學葉瀾教授在其主持的“新基礎教育”研究中，對教學的總方法強調“長程兩段整體設計”，即第一段“教結構”、第二段“用結構”。這與“深度學習”中強調新知與舊知結構關聯的核心思想不謀而合。在教授結構時，我們應關注學生具體的問題，解決學生的困難。基于學生的困難進行教材的再開發，根據內容結構的遷移教學，關聯設計教案，使學生能互動成長。

一、探究數學設計的方法關聯，明晰數學思維完整脈絡

數學教材一般把知識點分割成一節節“課”，按照循序漸進、螺旋上升的方式合理安排。這種安排，雖然有助于分解各個知識點的難度，但是也容易讓教師以“點”觀課，忽視知識點背后整體結構的意義。在教授新知時，教師可整體羅列相關舊知內容，對認知方法進行類比關聯。在設計時，教師可以采取關聯設計，即根據舊知與新知的聯系與區別，通過方法結構遷移設計的方式，喚醒學生已有的知識經驗，使學生形成整體認知。

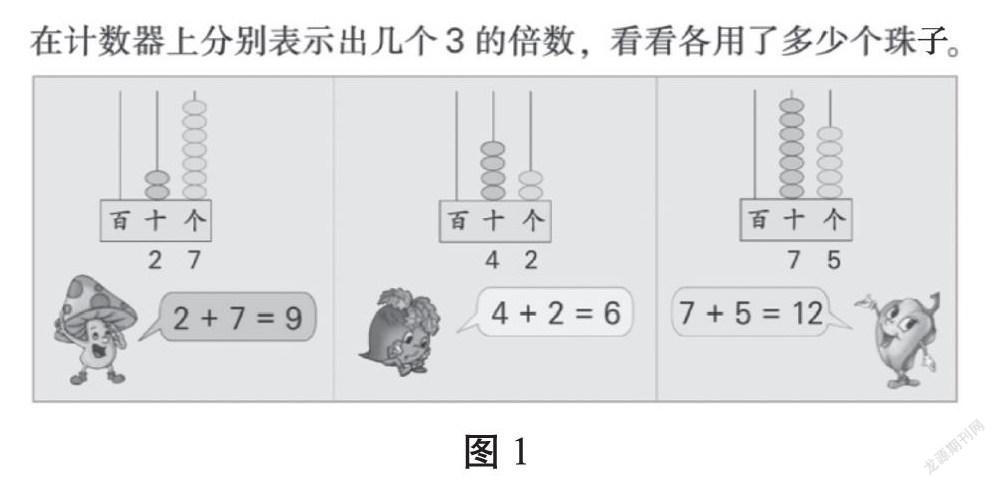
比如，教學“3的倍數的特征”一課時，學生們都牢記結論：數的各個數位相加得數為3的倍數，這個數就是3的倍數。但是，學生不知道為什么通過各個數位相加的得數就能判斷這個數是否是3的倍數。對于這個知識點，蘇教版教材是用撥珠子的方法來說明的（如圖1），人教版教材則是用“你知道嗎”這種信息拓展的形式告知學生（如圖2）。不管哪種形式，都是抽象籠統地告知，并未直指本質。

小學這個年齡段的思維特點是具體思維，教師教授這部分原理時應避免乏味灌輸，以圖形結合的方式講授會更加容易被學生接受。綜上所述，以低年級的數的組成的知識經驗為結構載體，筆者設計了如下過程（如圖3）：

引導學生明確一個百，每3個一分，最后會剩下一個1;一個十，每3個一分，最后會剩下一個1。也就是說，有幾個百，每3個一分，就多幾個1;有幾個十，每3個一分，就多幾個1。要看這個數能否被3整除，只要關注最后百位、十位、個位留下的1相加的總數能否被3整除即可。所以，我們判斷一個數能否被3整除，只要關注各個數位上的數的和能否被3整除即可。

在前期教學時，教師應給予適當的方法結構的鋪墊。如教學“因數與倍數”時，出示習題7×3+3×5=3×（7+5）與8×n+13×8=8×（13+n），引導學生發現左邊的算式根據乘法分配律，能改寫成右邊的算式，從而發現左邊的算式的和分別應是3的倍數和8的倍數。教學“2和5的倍數特征”時，幫助學生經歷一個百，每2個一分或者每5個一分，都能正好整除;一個十，每2個一分或者每5個一分，也正好能整除。所以，一個三位數，百位與十位上的數肯定能被2或5整除，判斷這個數能否被2或5整除，只需關注其個位能否被2或5整除即可。經過這兩節課前期方法結構的鋪墊，學生在探究“3的倍數的特征”時，就能有意識地進行平均分，從而發現規律。

可以看出，在教學“3的倍數的特征”一課之前，教師已經進行了大量的方法結構的滲透。在教學相同“類”課型的每一個階段，探究數理的思維邏輯的培養和數學表達的語言規范的培養就已經在慢慢形成。

二、探究感知材料之間的認知關聯，彰顯內容的廣聯性

在教學實踐時，常常會出現教師對學生認知的風格與方式認識不清，學情、學生學習動機分析不足等情況，導致對教學設計把握不到位，“深度學習”關聯教學設計困難。因此，要促發“深度學習”的產生，教師在設計教學時必然要充分考慮學生的學情，想學生所想、想學生所困，幫助學生建構完整的知識體系。數學認知結構的發展既包括數學思維的遞進過程，又包含數學知識結構的構建。小學數學關聯教學應以學生的認知發展過程與認知建構過程為發展經緯線，以學生自主探究、自覺發展為軸線，融通螺旋式發展。

比如，教學“認識梯形”一課時，蘇教版教材中出示了一組生活中梯形形狀的物體，如梯子、房頂等，根據找形狀相同點，直觀告訴學生什么是梯形。直接給予圖形的抽象方式屬于形式抽象，學生根據所給的這些對稱圖形，狹隘地認為只有像梯子形狀的圖形才稱為“梯形”，而對不等腰的梯形，特別是對兩條腰朝同一方向不同程度傾斜的梯形認識不深，往往認為這不是梯形。其實這就是學生的認識生長被割裂了，教師在讓學生感知材料、提煉梯形特征時，應考慮到各種梯形。如果能通過原來學習過的圖形來創造出梯形，知識結構能進行遷移，那么學生對梯形的特征感知印象會更加深刻。

教學初始，教師給學生提供四個剪好的圖形（如圖4），要求：在圖中添一條線，形成只有一組對邊平行的四邊形。

這四個圖形可以分成兩組，四邊形與三角形為一組，原圖中沒有平行的線段，添上一條線段創造出一組平行線，從而創造出梯形;長方形與平行四邊形為一組，在原來兩組對邊平行的基礎上破壞其中一組平行線，使圖形只有一組平行線，從而創造出梯形。一“添”一“破”看似簡單的操作，無不體現出教師設計的巧妙。四邊形與長方形的直角保證了資源中出現直角梯形;等腰三角形確保了資源中出現等腰梯形;平行四邊形則確保資源中出現兩條腰朝同一方向不同程度傾斜的梯形。設計感知材料環節時，教師充分考慮到學生的認知困惑點，以突破學生困惑點為出發點，精心選擇了四個圖形作為學生操作的感受梯形特征的感知材料。而在學生操作的過程中，教師充分預設可能出現的情況。如四邊形中過A點畫一條與線段CD平行的線段，可以構造梯形，也可以過C點畫一條與線段AB平行的線段構造梯形。當出現資源時，教師可以適時點撥：“一定要過A點才能畫線段CD的平行線嗎？”明確只要不超過A點，都可以。

學生的認知發展與他們的思維發展一一對應，一脈相承。教師通過這樣的教學，幫助學生在已有的基礎上對知識結構有清晰的認識。小學關聯教學應將知識的認知發展、知識的建構發展、知識的思維探究發展連接起來，形成有序、整體、動態、開放的教學系統。

教師通過“教結構”“用結構”的教學方法，長程設計教學方案，以促進學生“深度學習”為教學出發點，以提高學生學科核心素養為最高目標，不斷推進，做一個有使命感的教師。關聯融通的思維，才能真正實現“成人成事”的教育追求。

【參考文獻】

[1]蔣敏.核心問題引領，打造小學數學深度學習課堂[J].教育界，2020（6）.

[2]朱彩娟.促進學生深度學習的小學數學教學策略探析[J].新課程研究，2019（12）.

[3]金永梅.活動的深度決定學習的深度——對小學數學深度學習的幾點認識[J].數學教學通訊，2019（22）.

[4]陳秀華.淺談以問題為導向的小學數學深度學習[J].課程教育研究，2019（42）.

[5]席愛勇，何杰.結構關聯：小學數學結構化學習的學理探究——以《小數的意義》為例[J].淮陰師范學院學報（自然科學版），2018（4）.

[6]朱俊華，吳玉國. 基于單元整體的小學數學結構化教學[J].中小學教師培訓，2019（9）.

[7]鄧友祥.認知結構與小學數學教學中的遷移[J].教師之友，1997（4）.

[8]蔣敏杰.結構關聯，讓課前“熱身”持續升溫[J].小學數學教育，2015（6）.