高等數學與課程思政的融合方法探究

路云

摘 ?要：課堂是學校教育最重要的元素，在課堂教學過程中，教與學是基本關系，課堂教學是培養學生能力和素質的重要途徑。在課程思政背景下，文章對高等數學知識與數學發展史、生活哲理等融合的教學方式進行探究，力求將課程思政融入高等數學的教學中，在對學生進行理論知識傳授的同時，培育學生樹立正確的價值導向，激發學生主動學習的熱情。

關鍵詞：高等數學;課程思政;融合方法

中圖分類號：G642 ? ? 文獻標識碼：A ? ? 文章編號：1673-7164（2022）06-0161-04

百年大計，教育為本。其中高等教育是為祖國建設和培養高水平人才的重要途徑。高等數學是高校重要的公共基礎課，具有課時長、內容多、學生覆蓋面廣的特點，因此，如何潛移默化地將課程思政融入高等數學課堂以培養學生對高等數學的學習興趣，把高等數學教學和對學生素質的教育有機結合，使學生在課堂上既能有效地學到知識又能樹立起正確的世界觀尤為重要。本文通過對高等數學中思政元素的挖掘、提煉和案例教學的實踐來實現激發學生主動學習、主動探索的意識，實現對學生價值觀的引領。

一、課程思政融入高等數學課程教學的必要性

習近平總書記于2020年3月18日主持召開學校思想政治理論課教師座談會，深刻闡明學校思政課的重要意義。同年教育部印發《高等學校課程思政建設指導綱要》（以下簡稱《綱要》），《綱要》明確指出全面推進課程思政建設是落實立德樹人根本任務的戰略，落實立德樹人根本任務，必須將價值塑造、知識傳授和能力培養三者融為一體、不可割裂。全面推進課程思政建設，就是要寓價值觀引導于知識傳授和能力培養之中，幫助學生塑造正確的世界觀、人生觀、價值觀，這是人才培養的應有之義，更是必備內容。課程思政要緊緊抓住教師隊伍“主力軍”、課程建設“主戰場”、課堂教學“主渠道”，讓所有高校、所有教師、所有課程都承擔好育人責任，“守好一段渠、種好責任田”，使各類課程與思政課程同向同行，將顯性教育和隱性教育相統一，形成協同效應，構建全員、全程、全方位育人大格局。

高等數學是大學的基礎課程，課程本身具有抽象性和較高的邏輯性，導致其融入課程思政相比其他課程的難度更大。因此，對高等數學課程思政教學的研究，對培養具有較高綜合素質和獨立思考能力的創新型人才具有非常重要的現實意義。

在傳統的高等數學教學中[1]，授課老師基本上以“定義—定理—證明—推論”的方式教學，因課程邏輯性強、理論性強、知識點密，導致很多學生認為高等數學的知識晦澀難懂，自然而然對高等數學以及高等數學課堂望而生畏。為了改變這種課程教學模式，消除學生對高數課堂的畏懼，使他們發現和認識數學的美，如何在課堂教學中更好地將思政元素融入高等數學的教學就顯得非常迫切和必要。

二、將數學發展史引入高等數學的教學中

眾所周知，高等數學是建立在極限的思想上，圍繞著微積分原理建立起來的。早在戰國時期，我國莊子的無限理論“一尺之棰，日取之半，萬世不竭。”就蘊含了極限的思想。公元263年的魏晉時期，著名數學家劉徽在《九章算術注》中創立了割圓術[2]，他提出“割之彌細，所失彌少，割之又割，以至于不可割，則與圓合體而無失矣”的重要極限思想，并用割圓術計算了3072邊形面積，求得了圓周率，將圓周率精確計算到小數點后三位，劉徽在割圓術中提出的極限思想及結論比歐洲早了一千多年。南北朝時期的數學家祖沖之和祖暅，沿用劉徽的思想，在求“牟合方蓋”的體積時，于5世紀末提出了體積計算原理：“冪勢既同，則積不容異”，這就是祖暅原理。祖暅原理的發現比西方類似的原理早了一千一百多年;祖沖之是世界上第一位將“圓周率”精算到小數點后七位的科學家，他提出的“祖率”比歐洲要早一千多年，直到17世紀，意大利數學家卡瓦列里才得出相似的結論。這些數學史料都是中華民族的驕傲。近代數學史上，華羅庚和陳景潤這對師生的成就占據著舉足輕重的地位，華羅庚在多復變函數論，典型群方面的研究領先西方數學界十多年;陳景潤發表的陳氏定理成為哥德巴赫猜想研究上的里程碑。

通過回顧數學歷史，緬懷增強科學家的奉獻精神，學生不僅能了解中國數學的輝煌歷史，還能增強愛國情懷，進而在以后的學習和工作中發憤圖強，為建設祖國而加倍努力。將愛國情懷融入高等數學課程教學中，不僅可以激發學生們的愛國情懷，還能激發學生的學習動力，培養學生的創新思維，提升學生的數學研究能力。

三、挖掘高等數學中蘊含的哲理

課程思政融入高等數學，并不是新開一門課程，也不是每節課、每個章節都強行融入思政元素，而是可以結合知識點進行靈活融入，在潛移默化中培養學生高尚的情操，將育人和育才相統一。

高等數學中內含豐富的哲理，如：

（1）在講解函數極限的定義[3]■時，如果A代表學生的人生目標，x就代表為此目標所做的不懈努力和奮斗，只有當x無限向x0靠近時，f（x）才會無限向A靠近，所以要實現自己的人生目標就要有鍥而不舍的精神，堅持不懈的努力。

（2）在講解函數極限的局部有界性時，可以引用“不識廬山真面目，只緣身在此山中”來詮釋極限的局限性，通過在抽象的數學課堂中引入中華詩詞來陶冶學生的情懷，同時彰顯中國文化的價值。

（3）在講極限存在準則時，可以結合（1+0.01）365和（1-0.01）365的兩個結果為37.8和0.03來講，并得出結論：積跬步以至千里，積懶惰以致深淵，要時刻保持與時俱進，因為那些每天只比你努力一點的人，最終會將你拋開不只一點。

（4）在講解函數的間斷性與連續性時，通過講解連續點與間斷點的定義告訴學生只有訂立目標和方向是正確的，當你為之努力拼搏時，才能夠逐漸接近并最終實現目標，而間斷的點就好比定錯了目標和方向，當你認為自己已經無限趨近于目標的時候才發現你和目標之間是不連續的，因此選擇正確的目標和方向并為之努力才能使自身得到連續的、有利的發展。

（5）在講解無窮小和無窮大的知識點時，可以通過墨子說的“窮，或不容尺，有窮;莫不容尺，無窮也”，與墨子分析的“有窮”“無窮”的概念，得到無窮小和無窮大的辯證關系，并通過無限個無窮小的和不一定是無窮小的結論告訴學生們要“不以善小而不為，不以惡小而為之”，量變引起質變，而生活是由一件件小事組成的，教師應鼓勵學生在日常學習中注重知識的積累，享受學習的過程。

（6）在講函數的定積分時[4]，可以把人的一生看作一條曲線，人的年齡是橫坐標，人實現的價值是縱坐標，整個人生的成就就是曲線的積分，人生的起點無法決定，但可以決定自己人生曲線的走向，決定曲線斜率的大小，從而努力讓自己人生的曲線積分達到最大值。這就告訴學生在成長過程中，要以有限積蓄無限，以量變積蓄質變，以“十年磨一劍”堅韌不拔的精神，在一點一滴的積累中提高自身綜合素質，錘煉奮斗精神，實現人生價值。

（7）在講不定積分的第一類換元法（即湊微分法）時，對于同一道例題可以引導學生采用直接積分法和湊微分法兩種方法進行求解，培養學生邏輯推理能力，鍛煉學生的開放創新思維，使學生明白，在今后的生活工作學習中，要從多角度思考問題，并靈活處理，才可以做到事半功倍。

這些高等數學中的知識點都引申出了人們對人生、社會和生活的正確態度，能夠激發學生的思想碰撞和情感體驗，實現對學生價值觀的正確引領。

四、高等數學教學與多學科有機融合

將高等數學知識與不同專業知識相結合，提倡“從專業中來到專業中去”，即以實例的形式給出高等數學的知識點可以應用到專業課的哪些方面，讓學生切身體會到學習數學的實用性。

案例教學法[5]是最直接、最直觀的將數學理論與應用案例相結合的教學方法，也最能提高學生學習的主動性。如：

（1）在講解“導數”問題時，可以和水利工程專業中引入水渠水閘壓力問題公式dF=pds相結合;也可以和經濟管理專業中總成本函數的導數是邊際成本函數，在某點處總成本的導數是該點的邊際成本等實際問題中應用的導函數相結合，讓學生充分了解數學在專業課中的相關應用，體會數學的有用性。

（2）在講解可分離變量微分方程問題時，可以和環境專業林區原貌恢復的預測問題中需要講解的Logistic模型相結合[6]，通過講解讓學生體會在森林資源、生活資源的不斷改變下，熱愛自然、享受自然、保護自然的必要性，國家提出的“綠水青山就是金山銀山”政策的正確性和迫切性。

（3）在講解無窮級數中數列求和的知識點時，可以結合銀行儲蓄的復利問題舉例和學生一起探討利息的計算方法，讓學生在自己計算的過程中發現“利滾利”的可怕，同時指出“校園貸”“小額貸”等帶來的嚴重后果，引導學生養成理性消費的習慣，遠離非法貸款，建立正確的消費觀和價值觀。

（4）在講解導數應用中利用泰勒公式計算誤差的知識點時，可以結合2018年10月建成竣工的世界上最長的大橋——港珠澳大橋的建設過程進行講解[7]。港珠澳大橋是世界建筑史上投資最大、技術最復雜、建設要求及標準最高的工程，這座大橋是我國完全自主設計并完成的，為了將6.7公里長的外海沉管隧道順利鋪設，需要將排水量超過75000噸、每節管長180米的沉管在海平面以下13米至48米不等的深度進行海底無人對接并要將對接誤差控制在2厘米以內，我國當時對這項技術掌握程度為零，為了完成計劃，港珠澳大橋島隧工程項目總經理、總工程師林鳴帶領自己的團隊迎難而上，刻苦鉆研，最終攻克了這個技術難關，并將安裝誤差降低到了2.5毫米的程度。這個例子不僅說明了控制誤差、精益求精的重要性，也給學生強調了泰勒公式在誤差計算過程中的重要性[8-10]。

這些案例的講解都充分表明：高等數學的知識是在解決實際問題的過程中產生的并不斷進步和發展的，在生活中也只有像求解數學問題一樣，抓住矛盾的根源，將未知轉化為已知，對困難和問題進行不斷地化解，才能找到問題的突破口，戰勝困難，獲得進步和提升。教師應引導學生學習當代中國科研人員的鉆研精神，進而激發學生對新知識的探索精神和探索意識。

五、高等數學課程思政實施效果

為了更好地將課程思政融入高等數學的教學中，實現真正的理論與實際相結合，本研究通過調查問卷，調研北京科技大學天津學院大一到大四的部分學生對高等數學融入課程思政的了解情況，回收有效問卷1297份，受訪者學段分布如圖1：

■

圖1 受訪學生學段分布情況

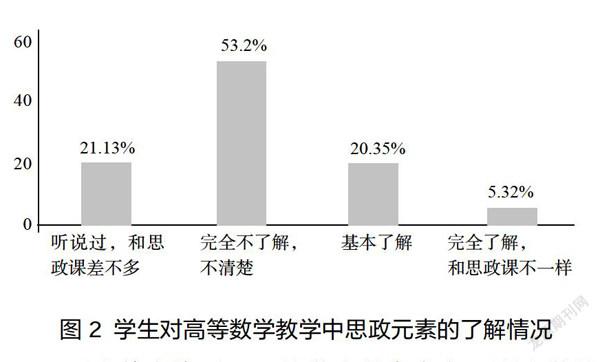
“學生對高等數學教學過程中的思政元素是否了解”一問中，有53.24%的學生表示完全不了解、不清楚，情況統計如圖2所示：

■

圖2 學生對高等數學教學中思政元素的了解情況

而這其中將近90%的學生是來自大一剛入學的新生;有85.96%的學生認為高等數學的教學過程中應該融入思政元素;有70.37%的學生非常愿意接受思政教育;有74.15%的學生認為課堂思政的融入能給予他們積極的思想指導，能幫助他們端正待人處事的態度和方式;有85.65%的學生認為課程思政可以幫助他們樹立正確的世界觀、人生觀和價值觀;有78.4%的學生表示，結合課程具體知識和案例穿插性地講授思政內容是他們希望的融合方式。

上述的統計數據和統計結果表明，學生對課程思政教學改革有真實的需求和迫切的渴望，也印證了將課程思政融入高等數學課堂的必要性、正確性和緊迫性。

六、結語

高等數學教育也是一種文化教育，其目的是提升學生的數學素養。只有把高等數學教育同數學的發展史相結合，讓學生在認識數學文化價值的過程中得到數學語言規范、標準潛移默化的熏陶，才能提升學生的數學素養[11-13]。

高等數學是大學的基礎學科，將課程思政融入高數課堂，可以把傳統的數學教育提高到數學文化教育的層次，教師切實貫徹教書育人、德育為先的教學理念，才能充分發揮全方位育人的教育教學能力，真正做到顯性教育與隱性教育互相融合，并為最終實現學生素質的全面提升和可持續發展奠定良好的基礎。

參考文獻：

[1] 劉黎明，楊寧. 學習科學視域下大學生深度學習能力的培養[J]. 華北水利水電大學學（社會科學版），2018（04）：106-109.

[2] 徐萍. 卓越人才培養中高等數學“課程思政”的思考[J]. 課程教育研究，2018，32（01）：1.

[3] 蔣艷，鐘艷，黃愛武. 高等數學課程思政案例教學探討[J]. 科教文匯，2018（09）：87-89.

[4] 劉淑芹. 高等數學中的課程思政案例[J]. 教育教學論壇，2018（52）：45-46.

[5] 逢世友，苗連英. 以本原問題驅動高等數學創新教學模式改革[J]. 教育現代化，2015，5（10）：177-178.

[6] 王培. 大學數學深度學習過程的一般模型研究[J]. 科教導刊，2020（11）：120-122.

[7] 張寧，王偲. 高等數學課程引入“課程思政”的思考與方法探討[J]. 教育現代化，2019，6（79）：255-256+259.

[8] 劉震，孫沖. 淺析“課程思政”融入高等數學教學的方法探究[J]. 科教導刊-電子版（上旬），2020（07）：190-191.

[9] 焦慧平，徐自立. 課程思政融入高等數學課程的探索和實踐[J]. 湖北開放職業學院學報，2021（07）：74-75.

[10] 曹鳴宇，張金艷，張麗，等. 融入課程思政理念的高等數學課程教學案例[J]. 當代教育實踐與教學研究（電子刊），2020（15）：88-89+93.

[11] 李英芳，閆超. 高職院校數學思政課教學存在的問題及策略初探[J]. 中國多媒體與網絡教學學報：電子版，2020（02）：174-175.

[12] 胡水玲，張團結. “課程思政”背景下高職高等數學教學設計與教學方法研究[J]. 河南教育（職成版），2020（03）：23-24.

[13] 王雅萍. 基于課程思政理念的高等數學教學改革探索[J]. 湖北開放職業學院學報，2020，33（02）：108-110.

（薦稿人：徐美林，北京科技大學天津學院副教授）

（責任編輯：陳華康）