線性代數(shù)案例教學(xué)實(shí)踐與探索
楊立星 李玉霞

摘 要:本文從案例教學(xué)的角度探索線性代數(shù)課程的教學(xué),通過(guò)引入與實(shí)際有關(guān)的案例,可以有效降低課程的抽象性和理論性,加強(qiáng)應(yīng)用性,引起學(xué)生學(xué)習(xí)本門(mén)課程的興趣,提高課程的教學(xué)質(zhì)量。
關(guān)鍵詞:線性代數(shù);案例教學(xué);行列式;矩陣;線性方程組
一、概述
線性代數(shù)課程是一門(mén)重要的公共基礎(chǔ)課程,為經(jīng)管類、理工類學(xué)生學(xué)習(xí)專業(yè)課程提供必要的知識(shí)儲(chǔ)備,也是各專業(yè)學(xué)生升學(xué)考試的考試科目,本門(mén)課程的重要性不言而喻。另一方面,和其他數(shù)學(xué)課程相比,本門(mén)課程在多數(shù)高校里面學(xué)時(shí)短、內(nèi)容抽象、理論性很強(qiáng),學(xué)生學(xué)習(xí)本門(mén)課程具有一定的難度。
通過(guò)引入有實(shí)際背景的案例或蘊(yùn)含課程思政元素的案例,可以有效地降低課程的抽象性,而且可以讓學(xué)生認(rèn)識(shí)到課程的重要性,培養(yǎng)學(xué)生理論聯(lián)系實(shí)際的能力,達(dá)到“學(xué)以致用”“立德樹(shù)人”的目的。從而提高學(xué)習(xí)本門(mén)課程的興趣和學(xué)習(xí)的主觀能動(dòng)性,提高本門(mén)課程的教學(xué)質(zhì)量,為學(xué)生后續(xù)的學(xué)習(xí)打下良好的基礎(chǔ)。
二、案例舉例
(一)案例1:線性方程組、克拉默法則的應(yīng)用
《九章算術(shù)》在公元一世紀(jì)左右成書(shū),在書(shū)中第8章方程中提到線性方程組,并給出了求解方程組的方法。書(shū)中提到谷物稱重問(wèn)題:在已有的三種谷物中,如果第一種谷物的數(shù)量有3袋、第二種谷物的數(shù)量有2袋、第三種谷物的數(shù)量有1袋,以上三種谷物重量總計(jì)是39個(gè)重量單位;如果第一種谷物的數(shù)量有2袋、第二種谷物的數(shù)量有3袋、第三種谷物的數(shù)量有1袋,以上三種谷物總重量總計(jì)是34個(gè)重量單位;如果第一種谷物的數(shù)量有1袋、第二種谷物的數(shù)量有2袋、第三種谷物的數(shù)量有3袋,以上三種谷物總重量總計(jì)是26個(gè)重量單位。請(qǐng)問(wèn),每種谷物一袋重量是多少?
解:三種谷物重量分別設(shè)為:x,y,z,則可建立線性方程組:
利用克拉默法則可解的:x=374,y=174,z=114。
通過(guò)這個(gè)案例,弘揚(yáng)了中國(guó)文化,使學(xué)生認(rèn)識(shí)到我國(guó)文化的博大精深和先人的聰明智慧,增強(qiáng)了學(xué)生的民族自豪感和文化自信息、愛(ài)國(guó)情懷。
(二)案例2:行列式的應(yīng)用
(三)案例3:經(jīng)濟(jì)學(xué)中的應(yīng)用案例
1.矩陣?yán)碚摰膽?yīng)用:列昂惕夫投入產(chǎn)出模型
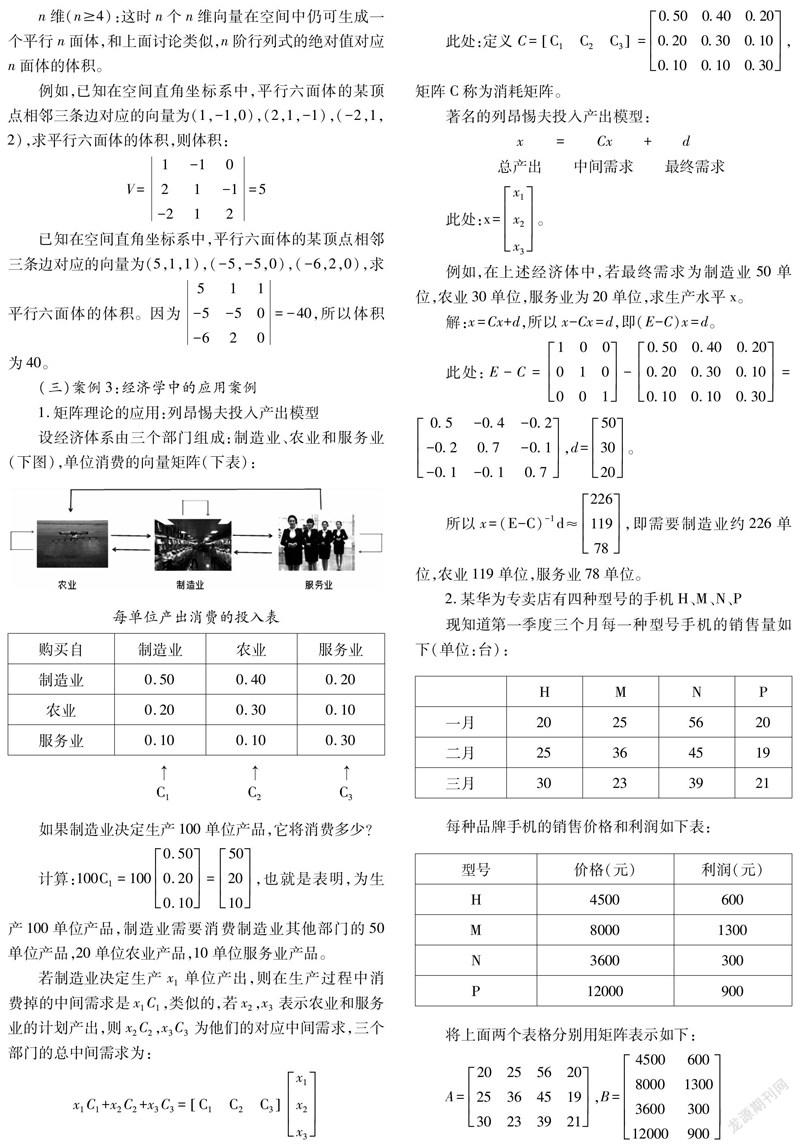
設(shè)經(jīng)濟(jì)體系由三個(gè)部門(mén)組成:制造業(yè)、農(nóng)業(yè)和服務(wù)業(yè)(下圖),單位消費(fèi)的向量矩陣(下表):
如果制造業(yè)決定生產(chǎn)100單位產(chǎn)品,它將消費(fèi)多少?
計(jì)算:100C1=1000.500.200.10=502010,也就是表明,為生產(chǎn)100單位產(chǎn)品,制造業(yè)需要消費(fèi)制造業(yè)其他部門(mén)的50單位產(chǎn)品,20單位農(nóng)業(yè)產(chǎn)品,10單位服務(wù)業(yè)產(chǎn)品。
若制造業(yè)決定生產(chǎn)x1單位產(chǎn)出,則在生產(chǎn)過(guò)程中消費(fèi)掉的中間需求是x1C1,類似的,若x2,x3表示農(nóng)業(yè)和服務(wù)業(yè)的計(jì)劃產(chǎn)出,則x2C2,x3C3為他們的對(duì)應(yīng)中間需求,三個(gè)部門(mén)的總中間需求為:
78,即需要制造業(yè)約226單位,農(nóng)業(yè)119單位,服務(wù)業(yè)78單位。
2.某華為專賣(mài)店有四種型號(hào)的手機(jī)H、M、N、P
現(xiàn)知道第一季度三個(gè)月每一種型號(hào)手機(jī)的銷售量如下(單位:臺(tái)):
通過(guò)上面矩陣的乘積可以看出一月、二月、三月該手機(jī)專賣(mài)店的銷售總額分別為731600元、790500元、711400元,銷售總利潤(rùn)分別為79300元、92400元、78500元。
(四)案例4:逆矩陣在密碼學(xué)中的應(yīng)用
建立26個(gè)英文字母與數(shù)字之間的一一對(duì)應(yīng)關(guān)系:
通過(guò)這個(gè)矩陣,巧妙地引出“1921”“1949”兩個(gè)重要年份和兩個(gè)一百年,引出思政元素,增加學(xué)生對(duì)現(xiàn)在和平年代來(lái)之不易的認(rèn)識(shí)和當(dāng)下國(guó)家發(fā)展的自豪感。
(2)從馬克思主義哲學(xué)思想出發(fā),挖掘思政元素。例如在講解矩陣和行列式的定義時(shí),因?yàn)閷W(xué)生經(jīng)常將行列式和矩陣表示方法混淆,為了讓學(xué)生認(rèn)識(shí)兩個(gè)概念的本質(zhì),行列式本質(zhì)上是一個(gè)“數(shù)”,而矩陣是一個(gè)“表格”,通過(guò)哲學(xué)概念“現(xiàn)象與本質(zhì)”加深對(duì)行列式與矩陣定義的認(rèn)識(shí)。又如,在講解矩陣的初等變換時(shí),可以引入“變與不變”的哲學(xué)概念,對(duì)一個(gè)矩陣進(jìn)行初等行變換,矩陣雖然發(fā)生了變化,但是矩陣的秩、矩陣對(duì)應(yīng)的齊次線性方程組的解均不發(fā)生變化。
結(jié)語(yǔ)
通過(guò)引入有實(shí)際背景的案例或蘊(yùn)含課程思政元素的案例,可以讓學(xué)生認(rèn)識(shí)到線性代數(shù)本門(mén)課程的廣泛應(yīng)用,通過(guò)實(shí)際案例,學(xué)生更容易地理解相應(yīng)的理論,提升了用理論知識(shí)解決實(shí)際問(wèn)題的能力,達(dá)到了課程育人的目的。
參考文獻(xiàn):
[1]David C.Lay.線性代數(shù)及其應(yīng)用[M].機(jī)械工業(yè)出版社,2017.
[2]羅增儒.行列式的簡(jiǎn)單應(yīng)用[J].數(shù)學(xué)通報(bào),1983(07).
[3]楊立星.行列式的幾個(gè)應(yīng)用[J].數(shù)學(xué)學(xué)習(xí)與研究,2013(01).
[4]同濟(jì)大學(xué).高等數(shù)學(xué)[M].高等教育出版社,2017.
[5]李乃華,等.線性代數(shù)及其應(yīng)用[M].北京:高等教育出版社,2006.
[6]張猛,賈麗娜,于金倩,王芳.應(yīng)用型本科環(huán)境下線性代數(shù)課程教學(xué)改革探究[J].教育教學(xué)論壇,2017.
[7]何郁波,程婧嬌.高等代數(shù)案例教學(xué)中幾個(gè)教學(xué)案例的設(shè)計(jì)[J].高師理科學(xué)刊,2017.
[8]江蓉,王守中.矩陣的秩在線性代數(shù)中的應(yīng)用及其教學(xué)方法探討[J].西南師范大學(xué)學(xué)報(bào):自然科學(xué)版,2012(8).
[9]狄勇婧.面向?qū)嶋H工程應(yīng)用的線性代數(shù)教學(xué)[J].教育教學(xué)論壇,2017(26).
基金項(xiàng)目:2021年度山東省青少年教育科學(xué)研究院,山東省教育教學(xué)改革研究項(xiàng)目“應(yīng)用型高校《概率論與數(shù)理統(tǒng)計(jì)》課程思政育人機(jī)制的探索與實(shí)踐”(21JG169)
作者簡(jiǎn)介:楊立星(1986— ),男,漢族,山東東平人,講師,研究方向:高等數(shù)學(xué)教學(xué)。

