從直觀想象到邏輯抽象： 基于GeoGebra的立體幾何教學

【摘 要】立體幾何的教學，需要引導學生在直觀感知、操作確認中發展空間想象能力，在度量計算、推理論證中提升邏輯抽象能力。以GeoGebra為平臺的立體幾何教學，可以創設情境，為概念理解提供直觀;變換視角，為問題解決尋求路徑;聯系推理，為規律論證啟發思路;交流分享，為自主學習創造機會。

【關鍵詞】立體幾何;GeoGebra;數學教學;直觀想象;邏輯抽象

【中圖分類號】G633.6? 【文獻標志碼】A? 【文章編號】1005-6009（2022）27-0015-04

【作者簡介】張加紅，江蘇省常州市田家炳高級中學（江蘇常州，213001）教師，高級教師，江蘇省首屆師德模范，江蘇省“五一勞動獎章”獲得者。

立體幾何是研究現實世界中物體的形狀、大小與位置關系的，雖然三維世界更貼近生活實際，但囿于空間想象力和表達手段的欠缺，尤其是空間圖形的平面表達（直觀圖）的制約，立體幾何一直是高中數學教與學的難點。《普通高中數學課程標準（2017年版2020年修訂）》強調要讓學生學會“運用直觀感知、操作確認、推理論證、度量計算等認識和探索空間圖形的性質，建立空間觀念”[1]，這就需要發揮信息技術的動態可視化特性。

作為一款專為教與學而設計的動態數學軟件，GeoGebra內嵌計算代數系統和指令輸入方式，可以對幾何對象進行直接代數化處理，使數學教學更為方便快捷，從而實現“形”（Geometry）與“數”（Algebra）的完美融合，可以說“懂得GeoGebra，她就給你獨到眼光，讓你洞悉數學世界”[2]。

對應立體幾何的教與學，GeoGebra有專門的 3D Graphics繪圖區。在這一繪圖區，我們可以構建逼真的三維幾何體，并呈現不同視角下的線面位置關系（在幾何體旋轉滾動的過程中，線面自動虛實切換），構建“多元聯系表征”的立體數學情境，并且可以突破表象的制約深入學科內部洞悉數學本質，從而實現從直觀形象到邏輯抽象的升級。

本文以GeoGebra為平臺，通過具體的教學案例呈現從“形”到“數”的探索，從而破解立體幾何教學難點，提高學生的學科素養。

一、創設情境，為概念理解提供直觀

數學本質上是對概念的理解和運用，立體幾何中也有很多概念，但這些概念多是以柱、錐、臺、球等空間幾何體為載體而生成的。因此，“通過豐富的實物模型或利用計算機軟件呈現空間幾何體，幫助學生認識它們的結構特征”成為我們的重要任務。

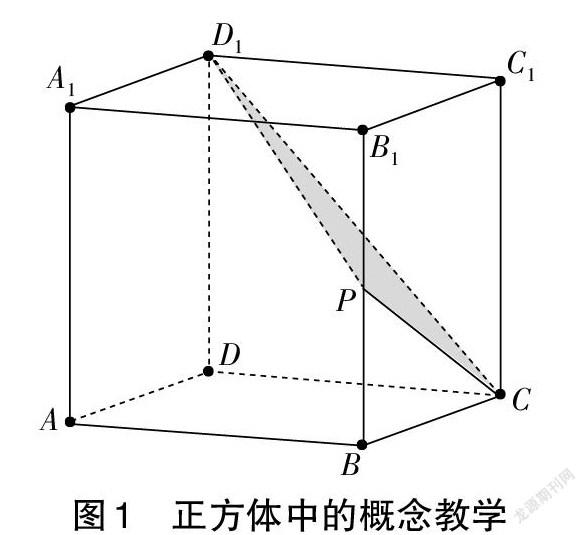
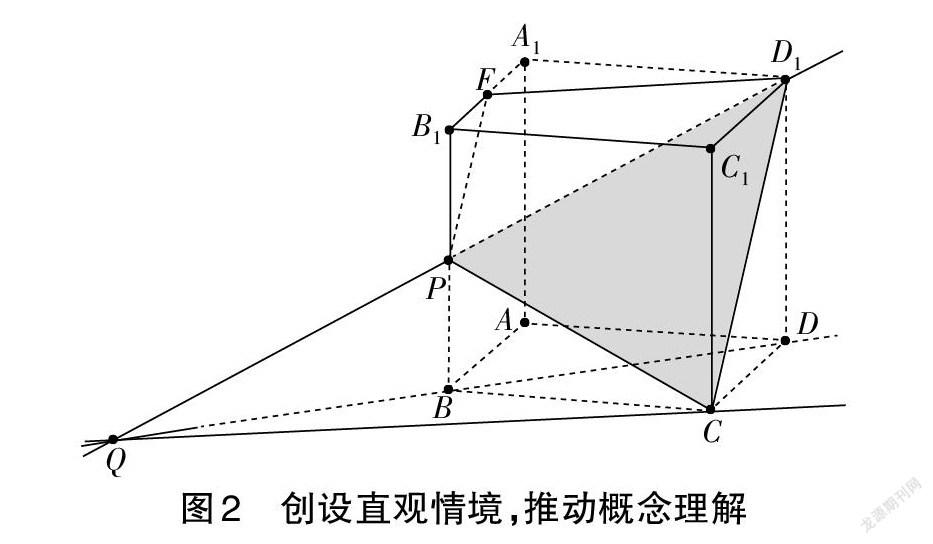
如教學異面直線的概念時，可以以圖1中正方體ABCD-A1B1C1D1（P為BB1的中點）為載體，展示棱之間的位置關系，引導學生發現相交、平行之外的另外一種關系——異面;辨析D1P、DB間的位置關系，可提煉出異面直線的概念（不同時處在任何一個平面內的兩條直線）。以空間圖形為背景來學習概念，因有具體的樣例支持而容易被學生接受。但這樣的教學也可能會因視覺受限而造成學生的思維障礙，如圖1中很多學生會誤以為D1P和AB相交。此時，教師可以利用GeoGebra創設更加直觀的情境，拖曳改變正方體的位置（見圖2），避免因視角受限而導致的錯誤理解。因此，立體幾何需要的是動態的直觀背景，以突破“橫看成嶺側成峰，遠近高低各不同”的視覺障礙。在此基礎上，對平面D1CP的認識應突破三角形的限制，也不限于等腰梯形D1CPF，而應在整個平面內構造平面D1CP與平面ABCD的交線——延長D1P、DB相交于點Q，QC即為兩平面的交線。

立體幾何的學習離不開圖形，考慮到空間圖形平面表示（直觀圖）的局限性，用信息技術來描述問題、理解概念、解決問題便顯得尤為重要。GeoGebra 3D Graphics繪圖區就是為立體幾何教學量身定制的軟件平臺，通過它能構建動態的直觀情境，不僅為概念生成提供豐富的樣例，更為概念理解提供想象空間。而空間觀念正是在這樣的“可視化”感知中得以落實，從而真正培養學生的數學思維，提高學生解決問題的能力。

二、變換視角，為問題解決尋求路徑

數學學科中，沒有方法就沒法解題，如何掌握數學解題的方法？張景中院士提出教育數學三原理，即“在學生頭腦里找概念，從概念里產生方法，方法要形成模式”[3]。對立體幾何的教學亦是如此，概念要能迅速轉化為方法，需要讓學生認識到問題的全貌，從而從整體上認識問題，在比較中找到最合理、最簡捷的解題路徑。

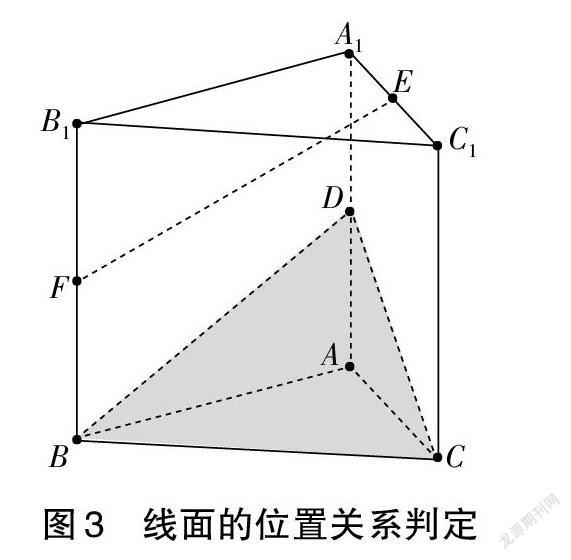
例1（線面的位置關系判定）：如圖3，三棱柱ABC-A1B1C1中，D、E、F分別為棱A1A、A1C1、B1B的中點，試判斷直線EF與平面BCD的位置關系。

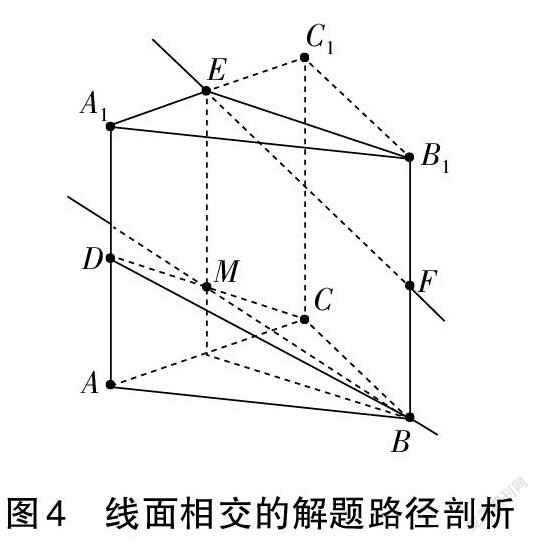
對照線面相交、線面平行的概念，判斷直線EF與平面BCD的位置關系的關鍵在于“在平面BCD內找到一條直線l與EF平行或相交”，而直線l與EF構成了另一平面α，因此解題的方向在于構造平面α。于是便有了圖4所示的解題路徑，構造平面BFE，與CD交于點M，因為EM∥FB且EM≠FB，可知EF與MB相交，這樣就可以說明直線EF與平面BCD相交。

不同的視角下，線面可能“呈現”不一樣的關系，因此變換視角的目的首先就是要破除可能有的圖形“欺騙”效應;同時轉變問題解決的思路，從概念出發反向思考，借助GeoGebra的表征優勢，讓MB顯而易見。這樣，解題過程從直觀走向抽象，在圖形與圖形關系中抽象出數學概念之間的關系，并用數學語言予以表征。

三、聯系推理，為規律論證啟發思路

立體幾何的學習離不開圖，基本方法是“直觀感知（識圖）—操作確認（畫圖）—度量計算（算圖）—思辨論證（證圖）”。一方面我們需要形成一些基本模型方便識別套用（如三垂線定理）;另一方面更需要形成一些問題解決觀念（如空間問題轉化為平面問題），將低維的問題升格到高維的視角，形成一般的方法和統一的思路。

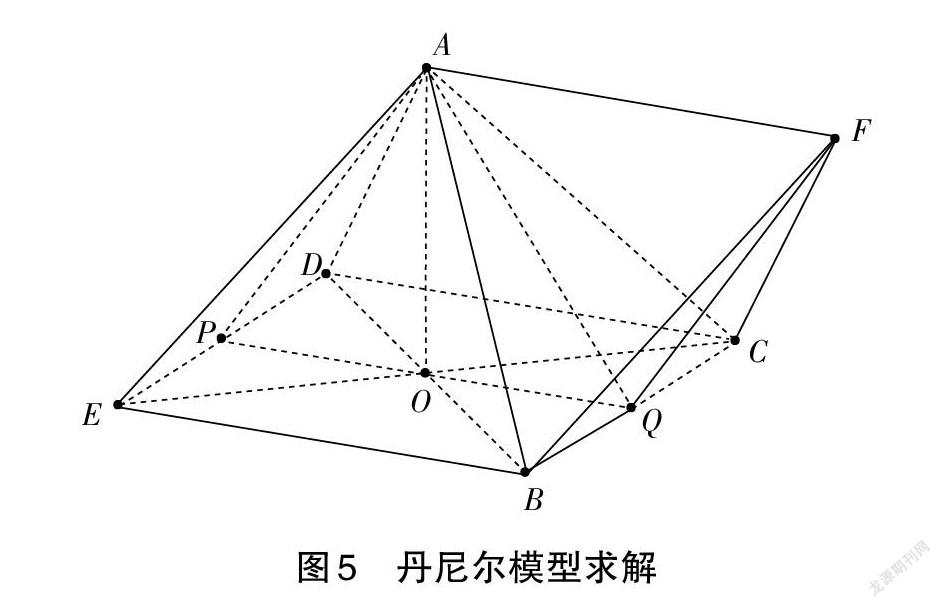
例2：如圖5，正四面體A-BCF和正四棱錐A-BCDE棱長均相等，求證：AF∥面BCDE。

這個問題其實就是1982年美國數學學會遇到的丹尼爾模型，解決這個問題的關鍵是將空間問題轉化為平面問題。[4]考慮到O點為正四棱錐底面的中心，于是構造平面OAF（與DE、BC的交點分別為P、Q），可知△APQ、△QAF為全等的等腰三角形，則不難證明AFQP為平行四邊形，這樣問題便可解決。

邏輯推理是數學素養的核心，立體幾何則是發展學生邏輯推理素養的重要載體。我們的教學目標并不是要建立結構完善、邏輯嚴密的立體幾何知識體系，而是引導學生在不斷深化對空間圖形的認識的過程中，通過類比、轉化等方法，發現和提出研究立體圖形位置關系的問題，實現由表及里、從定性到定量的深化，從而學會用數學的思維思考數學問題。

四、交流分享，為自主學習創造機會

GeoGebra可以為立體幾何的教學營造一個“探索數學、體驗數學”的真實環境，引導學生不再僅僅向書本、向老師學習數學，更可以向技術學習數學。例如，將圖5所示的情境上傳至GeoGebra鏡像網站，學生可在任何終端訪問https：//ggb123.cn/m/fw52baqx后進行實驗操作（無須下載安裝軟件）。

事實上，教育技術融合應用下的數學課堂，可以改變傳統教學中學生被動學習的狀態，學生從以往的聽眾變成了積極的參與者，真正成為課堂的主體。學生在教師引導下進行“再創造”，使其對數學有更深刻的認識，產生更強烈的求知欲，也進一步提高了學生學習數學的積極性。

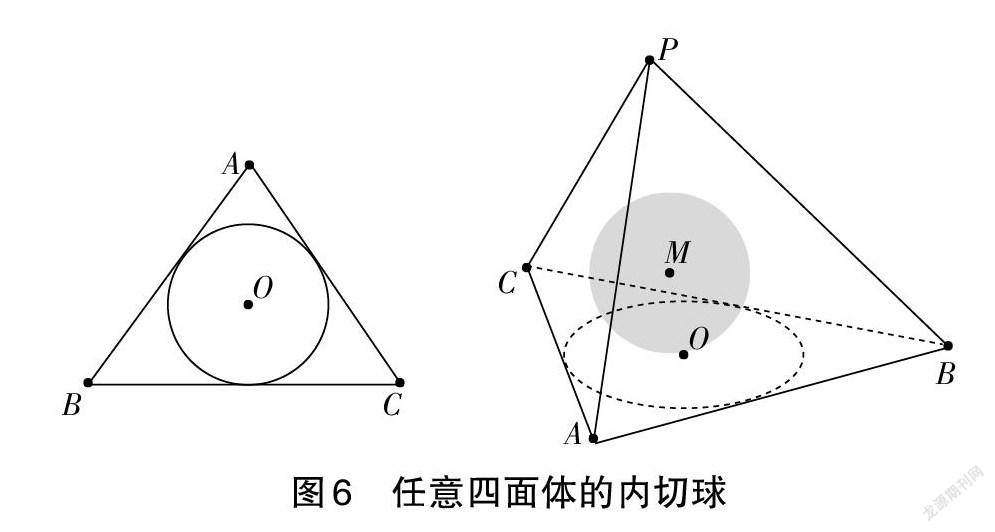
例3：從任意三角形的內切圓到任意四面體的內切球。

空間中的任意四面體可以類比平面中的任意三角形，既然任意三角形有內切圓，那么任意四面體就自然有內切球。面對學生“如何構造任意四面體的內切球”的追問，筆者并沒有直接回答問題，而是啟發他們運用類比的思路嘗試解決。

第一，用等積法計算半徑。S△ABC = S△OAB + S△OBC + S△OCA ? r = [2SAB+BC+CA] ，于是四面體中也有類似的計算，由VP-ABC =VM-ABC +? VM-PAB + VM-PBC + VM-PCA ，得R = [3VS1+S2+S3+S4]。

第二，以角平分面確定球心。三角形有三條角平分線，其交點為內切圓圓心;類似的，四面體有四個（二面）角平分面，于是可猜想角平分面的交點即為內切球的球心。這樣的猜想可以通過GeoGebra得到證實（先后輸入下列4個指令便可完成球心M的構造）：

l=平面（旋轉（A，角度（平面（A，B，C），平面（P，B，C））/2，直線（B，C）），B，C）;

m=平面（旋轉（B，角度（平面（B，C，A），平面（P，C，A））/2，直線（C，A）），C，A）;

n=平面（旋轉（C，角度（平面（C，A，B），平面（P，A，B））/2，直線（A，B）），A，B）;

M=交點（相交路徑（m，l），相交路徑（m，n））。

毫無疑問，信息技術的廣泛應用正在對數學教育產生深刻影響。于是，發揮技術優勢、推進新技術與教育教學的深度融合理應成為當前教育教學改革的重要課題。一方面我們需要讓技術賦能，在常態化應用中創新模式，讓學生經歷從具體到抽象的過程，既“看到”背后的“數據”更“看透”其中的數學“內容”，而數學的眼光、數學的語言、數學的思維恰可蘊含其中;另一方面，更要發揮技術的教育價值，從具體的教學內容出發，研究學生的認知難點和技術優勢，因為唯有對技術應用的創造性理解才有課堂教學的“游刃有余”。誠如《荀子》所言，“道阻且長，行則將至;行而不輟，未來可期”，我們因“心向往之”而扎根課堂，不懈前行。

【參考文獻】

[1]教育部.普通高中數學課程標準（2017年版2020年修訂）[S].北京：人民教育出版社，2020：27.

[2]張志勇.高中數學可視化教學：原則、途徑與策略——基于GeoGebra平臺[J].數學通報，2018（7）：21-24，28.

[3]張景中.張景中教育數學文選[M].上海：華東師范大學出版社，2021：5.

[4]李錦昱.丹尼爾·剪拼題·空間想象能力[J].高中數學教與學，2005（5）：48-49.